Сопротивление деталей орудий лова, имеющих форму пластины.
Форму пластины имеют, например, такие детали оснастки орудий лова, как траловые распорные доски и подъемные щитки.
Для пластины, расположенной под некоторым углом а к направлению движения, результирующая гидродинамических сил R может быть разложена на составляющие: силу лобового сопротивления Rx, подъемную (или распорную) силу Ry, боковую силу Rz. Значения составляющих рассчитываются по формулам:
где сх, су, cz — гидродинамические коэффициенты этих сил.
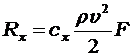 (1.3)
(1.3)
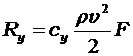 (1.4)
(1.4)
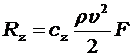 (1.5)
(1.5)
Значения коэффициента лобового сопротивления сх для квадратной или круглой пластины, плоскость которой расположена перпендикулярно направлению движения, в зависимости от числа Рейнольдса показаны в приложении 6. Удлинение пластины находится из выражения
l=a2/F. (1.6)
Для прямоугольной пластины
l =а/b, (1.7)
где а – размах пластины; b – ее хорда.
Гидродинамическое качество k пластины определяется из отношений:
k=Cylcx=Ry/RX: (1,8)
Значения гидродинамического качества плоской прямоугольной пластины при Л=0,5 в зависимости от угла атаки показано в приложении 8.
Коэффициент центра давления Cd1 находится из отношения
Cd1=х1d/b, (1.9)
где х1d — расстояние между передним ребром пластины и центром давления.
Вектор результирующей гидродинамических сил R в общем случае не проходит через начало координат и создает моменты относительно осей X,Y,Z. Момент Mz (относительно оси Z) находится из выражения
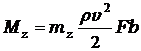 (1.10)
(1.10)
где тг — коэффициент гидродинамического момента.
Зависимости указанных гидродинамических коэффициентов от угла атаки для профилированных пластин индивидуальны для каждого профиля пластины и ее формы в плане.
Связь между значениями гидродинамических коэффициентов определяется выражением
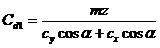 (1.11)
(1.11)
Сила сопротивления пластины, расположенной параллельно вектору скорости набегающего потока, находится по формуле
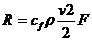 (1.12)
(1.12)
где Cj — гидродинамический коэффициент трения
Коэффициент трения Сf зависит от числа Рейнольдса. Для условия Re<104
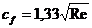 (1.13)
(1.13)
Для условий 106<Re<2*107
c;=0,074/Re1/5 (1.14)
В диапазоне. 104 <Re<106 коэффициент cf принимает промежуточные значения.
В соотношениях (1.15) и (1,16) число Re находится как
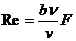 (1.15)
(1.15)
Для расчета сил трения также используются формулы: для условия Re<104
R= 0,7b -0,57Fv 1,5 (1.16)
и для условия 106<Re<2*107
R=2,3b-0,2Fv 1,8 (1.17)
Расчет подъемной силы Ry и силы лобового сопротивления Rx гидродинамических щитков, применяемых для оснастки тралов, аналогичен изложенным выше расчетам для пластины.
Для оснастки орудий лова применяются также тела и более сложных форм, чем рассмотренные выше (стяжные кольца кошелькового невода, поплавки и грузила в виде цилиндров с закругленными или конусообразными концами и т. д.).
Сопротивление деталей орудий лова, имеющих форму цилиндра.
Форму цилиндра имеют поплавки и грузила, применяемые для оснастки подбор кошельковых неводов, закидных неводов, плавных и ставных сетей. Близки к цилиндрической форме прямолинейные тросы, канаты и нитки.
Гидродинамические коэффициенты для цилиндра зависят от формы его сечения (круг, эллипс ...), Re, удлинения l (отношения длины l к диаметру d), угла атаки a.
Для кругового цилиндра значения гидродинамических коэффициентов находятся в три этапа. Сначала находится значение коэффициента Cб.у для цилиндра бесконечного удлинения (l>40) при расположении оси цилиндра перпендикулярно вектору скорости набегающего потока в зависимости от числа Рейнольдса. Зависимость Cб.y=f(Re) для цилиндра с круговым сечением показана в приложении 4. Re определяется из соотношения (1.2). Далее уточняется значение гидродинамического коэффициента с учетом его фактического удлинения:
Ск.У=Сб.уk(R). (1.18)
Данные о поправочном коэффициенте k(l) приведены в приложении» 5. Затем находятся гидродинамические коэффициенты подъемной силы су и лобового сопротивления сх в зависимости от угла атаки a:
CY, = CКY.sin2acosa; (1.19)
CХ = CKYsin2a. (1.20)
Ориентировочные значения коэффициентов сопротивления для цилиндров бесконечного удлинения при расположении оси перпендикулярно вектору скорости набегающего потока: для эллиптического сечения Сб.у=0,2; для цилиндра, имеющего в сечении форму тела наилучшего обтекания, Сб.у=0,026.
Качественно сопротивление прямолинейных тросов, канатов и ниток подчинено тем же закономерностям, что и сопротивление гладких цилиндров. Количественно значения гидродинамических коэффициентов этих тел отличаются существенно. Поэтому значения коэффициентов для цилиндра могут использоваться лишь в ориентировочных расчетах гидродинамических сил, действующих на прямолинейные тросы, канаты и нитки.
Гидродинамические коэффициенты для прямолинейных стальных тросов, расположенных под углом а к потоку, могут быть найдены по формулам:
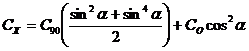 (1.21)
(1.21)
cУ=asin2acosa; (1.22)
cZ = ±bsin3acosa, (1.23)
где C90 — коэффициент сопротивления троса, ось которого расположена перпендикулярно направлению движения, его значение может быть принято равным 0,9—1,15; CO — коэффициент сопротивления троса, ось которого совпадает с направлением движения, его значение находится в пределах 0,02—0,03; а - эмпирический коэффициент, равный 0,92; b - эмпирический коэффициент, значение которого зависит от диаметра троса следующим образом:, для тросов диаметром 18—20 мм b = 0,65; для тросов диаметром 20—25 мм b = 0,65-1,0; для тросов диаметром больше 25 мм b = 1,0.
Формула (1.23) справедлива для стальных шестипрядных тросов. Знак «минус» здесь относится к тросам правой свивки, знак «плюс» — к тросам левой свивки. Таким образом, направления боковой силы Rz для тросов правой и левой свивок противоположны.
Характерную площадь F в этом случае следует вычислять как произведение хорды и диаметра каната.
Сопротивление сетей.Для расчета сил R сопротивления сетного полотна используется формула
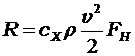 (1.24)
(1.24)
где Fн — площадь ниток сети, мг.
Для сети, расположенной перпендикулярно вектору скорости потока, коэффициент сх определяется по формуле
 (1.25)
(1.25)
. где F0—относительная площадь(сплошность) сети  .(1.26)
.(1.26)
Для ориентировочных расчетов в тех же целях могут использоваться формулы:
 (1.27)
(1.27)
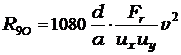 (1.28)
(1.28)
где Fr — габаритная площадь сети, м2; их, иу — горизонтальный и вертикальный посадочные коэффициенты.
Формула (1.27) справедлива для диапазона малых чисел Re (до 2·102) и больших значений относительной площади (Fo=0,3÷0,5).
Формула (1.28) соответствует постоянному значению CX = 2,2, что имеет место при относительной площади сети Fо=0,1÷0,4 в широком диапазоне числа Re (более 102).
Значение коэффициента сопротивления плоской сети сх, расположенной параллельно вектору скорости потока, определяется по формуле
СX=0,1Re 0.14 (1.29)
Для ориентировочного расчета сопротивления такой сети могут быть использованы также формулы:
Ro=18FГv2 (1.30)
Ro=18l-0.2FГ v1.75 (1.31)
где ℓ — длина сети, м.
Последнее выражение дает более точные результаты по сравнению с (1.31) при большой длине сети (50 м и более).
Для сети, расположенной под некоторым углом а к потоку воды, коэффициент сопротивления определяется выражением
Cх=0,04а-0,09. (1.32)
Формула (1.32) справедлива для следующих условий: Re= 103÷104; Fо = 0,04-0,3; а = 6÷14°.
Ориентировочное значение силы сопротивления сети, расположенной под углом и к направлению потока, может быть найдена с использованием формулы
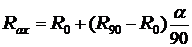 (1.33)
(1.33)
При набегании потока под углом а к плоскости сети помимо силы лобового сопротивления Rax возникает распорная (подъемная) сила сети Ray. Ориентировочные ее значения могут быть найдены по формуле
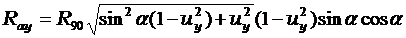 (1.34)
(1.34)
где иу — посадочный коэффициент по кромке сети, расположенный перпендикулярно потоку.
(Сопротивление однородной провисающей сети, расположенной перпендикулярно к вектору скорости набегающего потока, определяется формулой
RПC= R90Q, (1.35)
где R90— сопротивление плоской сети.
Q =l,6-2,96(L/S)+2,36(L/S)2, (1.36)
где L — хорда; S — высота сети.
(Сопротивление конусообразной однородной сети, основание которой перпендикулярно течению, находится по следующим формулам.
Для диапазона малых скоростей движения потока (0,1—0,8 м/с)
Rk= R90c, (1.37)
где R90— величина сопротивления плоской сети, расположенной перпендикулярно к потоку, площадь которой равна pD2/4.
Коэффициент c находится из выражения
c = 0,6 + 0,42L/D (1.38)
где L — длина образующей конуса; D — диаметр его основания. Выражение (1.38) справедливо для значений L/D<8.
Для диапазона больших скоростей движения потока (0,2— 4,5 м/с)
Rk=112Dl Q Fv2/3 (1.39)
где F — площадь основания конуса.
В формуле (1.40) эмпирические коэффициенты, D c, Q определяются выражениями:
D=11,7 (uхuу)2-10,8(uхuу) +3,4; (1.40)
l= 0,5 + 0,1(L/D); (1.41)
Q = 0,5+13,2 (d/a). (1.42)
По величине сопротивления сеть в форме кругового (а также усеченного) конуса эквивалентна равной по площади плоской сети, составляющей с вектором скорости тот же угол, что и образующая конуса. Поэтому для расчета сопротивления конуса и соответствующих условий его движения могут использоваться значения коэффициентов сх, определяемые из выражения (1.32).
Приведенные выше формулы для расчета сопротивления сетей применимы и в случаях, если они имеют неоднородную структуру (различные диаметры ниток, шаг ячеи, посадочные коэффициенты и т. д. на отдельных участках сети). Учет неоднородности структуры осуществляется путем использования в соответствующих формулах обобщенных характеристик и, d, F„ и т. д. Для расчета средних взвешенных значений характеристик используются формулы
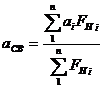 (1.43)
(1.43)
 (1.44)
(1.44)
 (1.45)
(1.45)
где i - порядковый номер пластины; п — общее число неоднородных пластин.
Сила сопротивления рыболовной сети произвольной формы, представляющей собой комбинацию элементов в виде плоской сети, сети с провисом, конусообразной сети и т. д., приближенно равна арифметической сумме сопротивления указанных сетных элементов.
Если сеть частично забита наносами, то ее сопротивление возрастает и может быть приближенно оценено по формуле
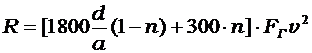 1.46
1.46
где n — отношение площади наносов на сети к ее общей площади.
Литература: [1], стр. 26-49
Пояснение по решению задач.
Задача 1.11.[2]
Ход решения:
1. Определяется сопротивление одного кухтыля по ф. 1.1.
Для этого
определяем площадь сечения шара F=f(d)
определяем плотность воды r=f(S,t) по приложению 1 [2]
определяем кинематическую вязкость воды n=f(S,t) по приложению 2 [2]
Определяем число Re по формуле1.2
Определяем СХ= f(Re) по приложению 3 [2]
2. Определяем сопротивление n кухтылей.
Задача 1.21.[1]
Ход решения:
Имеем дело с цилиндром бесконечного удлинения, расположенным перпендикулярно потоку.
1. Сопротивление рассчитывается по ф. 1.1. Для этого:
определяем площадь сечения цилиндра F=f(d,l)
определяем удлинение цилиндра l=l/d.
Определяем число Re по формуле1.2
Определяем СХ= f(Re) по по приложению 4 [2]
определяем плотность воды r=f(S,t) по приложению 1 [2]
Задача 1.38.[2]
Задача решается по формулам 1.3, 1.4
Задача 1.39.[2]
Задача решается по формулам 1.3, 1.4
Предварительно определяется удлинение пластины l=l/b, и по приложению 7 [2] находятся коэффициенты СХ и СY
Задача 1.60.[2]
Сопротивление сети определяем по формуле 1.24 .
Для сети, расположенной перпендикулярно вектору скорости потока, коэффициент сх определяется по формуле 1.25/
Диаметр нитки определяется из отношения 
Коэффициент uY определяется из отношения uX2+ uY2=1
Площадь нитей сети FН= FГ*FО
Число Рейнольдса находим по формуле Red=dv/n (формула ІІ-21 [2]).
Задача 1.126.[2]
Фигура, которую представляет собой мотённая часть трала является усечённым конусом. Её сопротивление считается как разность сопротивлений полного конуса ABE и малого конуса DCE (рис. 1)
Сопротивление конусов рассчитать по формуле 1.39. Значения а и d рассчитать как средневзвешенные (формулы 1.43, 1.44).
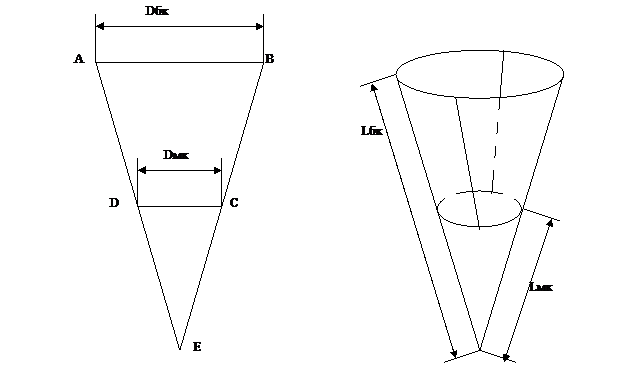
Рис.1
Вопросы для самоконтроля
1. какие элементы орудий лова имеют форму простых фигур.
2. Каков порядок расчета сопротивления шара, цилиндра, пластины?
3. Порядок расчета и основный формулы для определения сопротивления плоской сети.
4. Алгоритм расчета сопротивления конусной сети.
 Тема СИЛЫ ТЯЖЕСТИ И ТРЕНИЯ; УСИЛИЯ, РАЗВИВАЕМЫЕ РЫБОЙ
Тема СИЛЫ ТЯЖЕСТИ И ТРЕНИЯ; УСИЛИЯ, РАЗВИВАЕМЫЕ РЫБОЙ
Силы тяжести. Результирующая сил тяжести Р, действующая на орудие лова и его детали, направлена вертикально вниз. Результирующая гидростатических (архимедовых) сил D направлена вертикально вверх. Значения Р и D определяются по формулам:
P=gV, D=gBV(2.1)
где V — объем тела, м3; g — объемный вес тела, Н/м3; gB — объемный вес воды, Н/м3.
Вес тела в воде Q представляет собой равнодействующую сил Р и D, если последние находятся на одной вертикали, вычисляется по формуле
 или
или 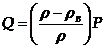 (2.2)
(2.2)
где r — плотность материала детали, кг/м3; rв — плотность воды, кг/м3.
Для сетеснастных материалов, поверхность которых имеет пористую структуру, следует отличать истинный объем изделия Vист и его внешний объем VBH. Сила тяжести таких изделий (ниток, веревок, канатов, сетей) может быть определена выражениями
Р = g Vист; Р = g ФVВН, (2.3)
где g Ф— фиктивный объемный вес изделия, Н/м3, а гидростатическая сила — из
D=yB Vист. (2.4)
Объемный вес материала ниток, канатов и сетей после предварительного экспериментального определения сил PhD вычисляется по формуле
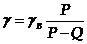 (2.5)
(2.5)
Объемный вес сетематериалов и их плотность r связаны:
g=rg, (2.6)
где g — ускорение силы тяжести, м/с2.
Средний объемный вес в воде g * ниток и канатов определяется из
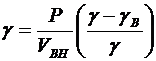 (2.7)
(2.7)
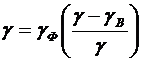 (2.8)
(2.8)
Силы трения.Сила трения при движении деталей оснастки по грунту (например, грунтропа) определяется выражением
F=Nf=Gf (2.9)
где N —реакция грунта; G — вес грузила в воде; f — коэффициент трения.
Держащая сила балласта на канатной оттяжке рассчитывается по формуле
 (2.10)
(2.10)
Держащая сила якорей определяется из выражения
F=kG (2.11)
где G — вес якоря; k — опытный коэффициент.
Усилия, развиваемые рыбой. Статическое усилие R0, развиваемое рыбой, рассчитывается по формуле
Ro=koPL-1/3 . (2.12)
Максимальное динамическое усилие R, развиваемой рыбой, находится из выражения
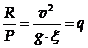 (2.13)
(2.13)
Необходимая величина упругого перемещения снасти для условия, при котором динамическое усилие, развиваемое рыбой, не должно превышать собственного ее веса, определяется соотношением
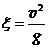 (2.14)
(2.14)
Вес рыбы в воде РВ связан с весом ее в воздухе. Р соотношением
РВ= (0,01-0,02) Р. (2.15)
Вертикальная потопляющая сила РП, создаваемая попавшей в орудие лова рыбой, приближенно оценивается выражением
PП = 0,07Р, (2.16)
где РП — потопляющая сила, создаваемая уловом.
Литература: [1], стр. 50-59
Пояснение по решению задач.
Задача 2.4 [2]
1. Сила плавучести рассчитывается по формуле 2.2
Для этого определяем плотность воды r=f(S,t) по приложению 1 [2]
Задача 2.8[2]
 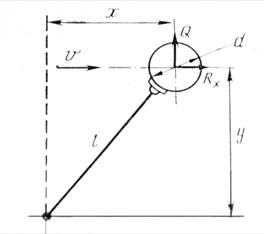 Рис. 2 Рис. 2 | Положение кухтыля (Рис. 2) определяется углом a, который можно определить из соотношений сил RX и Q: tg a= RX / Q Сила плавучести рассчитывается по формуле 2.2 [2]. Для определения плотности шара необходимо найти его объём V= 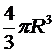 . RX рассчитывается по формуле 1.1 Для этого пределяем число Re по формуле1.2 , и СХ= f(Re) по приложению 3 [2] . RX рассчитывается по формуле 1.1 Для этого пределяем число Re по формуле1.2 , и СХ= f(Re) по приложению 3 [2] |
Задача 2.19[2]
Сила тяжести сети в воде определяется по формуле 2.2
плотность воды r=f(S,t) определяем по приложению 1 [2]
плотность материала сети определяем по приложению 14 [2]
2.62
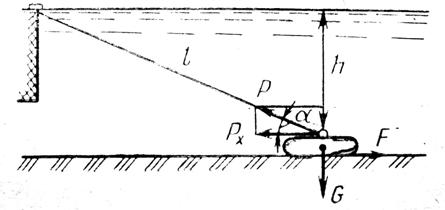 | Рис. 3 |
Масса груза G рассчитывается из формулы 2.10. В соответствии со схемой (Рис. 3), сила F должна быть не менее силы РХ – горизонтальной составляющей натяжения оттяжки. Для расчета РХ необходимо знать угол, который определяется из треугольника с катетом h и гипотенузой l.
Вопросы для самоконтроля
1. Как определить вес объекта в воде?
2. Как рассчитываются силы воздействия рыбы на орудие лова?
3. Что такое держащая сила якорей?
4. Как определить держащую силу балласта и грузил?
Содержательный модуль:
Механика гибкой нити.
