Формулы дифференцирования сложных функций
|
|
Рассмотрим нахождение производных сложных функций на конкретных примерах.
Пример 1.Найдите производную функции 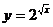 .
.
Решение. Функция 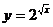 - сложная функция. Обозначим
- сложная функция. Обозначим 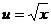 и придем к показательной функции
и придем к показательной функции 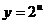 . Найдем ее производную по таблице производных сложных функций:
. Найдем ее производную по таблице производных сложных функций:
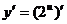 =
= 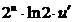 . Заменяя и через
. Заменяя и через 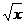 придем к производной вида:
придем к производной вида:
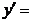
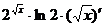 =
= 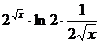 =
= 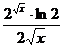 .
.
Ответ: 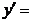
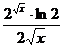 .
.
Пример 2. Найдите производную функции 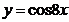 .
.
Решение. Функция 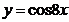 - сложная функция. Обозначим
- сложная функция. Обозначим 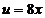 и придем к тригонометрической функции
и придем к тригонометрической функции 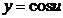 . Найдем ее производную по таблице производных сложных функций:
. Найдем ее производную по таблице производных сложных функций:
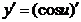 =
= 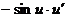 =
= 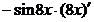 =
= 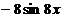 .
.
Ответ: 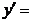
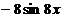 .
.
Пример 3. Найдите производную функции 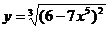 в точке
в точке 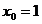 .
.
Решение. Сначала продифференцируем данную функцию. Функция 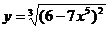 - сложная функция.Представим исходную функцию в виде степени:
- сложная функция.Представим исходную функцию в виде степени: 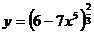 . Обозначим
. Обозначим 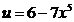 и придем к степенной функции вида
и придем к степенной функции вида 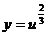 . Найдем ее производную по таблице производных сложных функций:
. Найдем ее производную по таблице производных сложных функций: 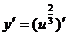 =
= 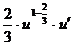 =
= 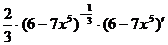 =
= 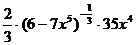 =
= 
= 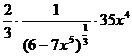 =
= 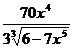 . Итак,
. Итак, 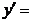
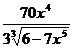 .
. 

Затем в найденную производную 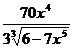 вместо аргумента подставим
вместо аргумента подставим 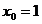 . Получим:
. Получим: 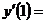
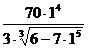 =
= 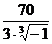 =
= 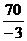 =
= 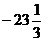 .
.
Ответ: 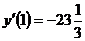 .
.
Пример 4. Найдите производную функции у=arcsinе2х .
Решение. Функция  - сложная функция. Обозначим
- сложная функция. Обозначим 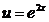 и придем к обратной тригонометрической функции
и придем к обратной тригонометрической функции  . Найдем ее производную по таблице производных сложных функций:
. Найдем ее производную по таблице производных сложных функций: 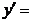 (arcsin u)' =
(arcsin u)' = 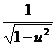 ·u' =
·u' = 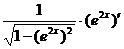 .
.
Однако, мы видим, что е2х тоже сложная функция. Обозначив 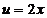 и придя к показательной функции
и придя к показательной функции 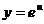 , найдем её производную по таблице производных сложных функций:
, найдем её производную по таблице производных сложных функций: 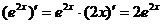 (здесь мы применили краткую запись решения).
(здесь мы применили краткую запись решения).
Получили, что 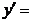
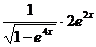 =
= 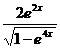 .
.
Ответ: 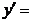
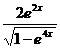 .
.
Список литературы:
1. Валуцэ И.И. Математика для техникумов на базе средней школы: Учебное пособие. / И.И. Валуцэ, Г.Д. Дилигул.– 2-е изд., перераб. и доп. – М.: Наука, 1989. – 576 с. – Глава 7, § 34, стр. 211-213.
2. Григорьев В.П. Элементы высшей математики: Учеб. для студ. учреждений СПО / В.П.Григорьев, Ю.А.Дубинский - М.: Издательский центр "Академия", 2004. – 320с. – Глава 6, §6.1, стр. 119 – 121.
3. Лисичкин В.Т. Математика: учеб. пособие для техникумов / В.Т. Лисичкин, И.Л. Соловейчик. – М.: Высш. школа, 1991. – 480 с. – Глава 4, §4, стр. 215– 217.
Раздел 3. ОСНОВЫ МАТЕМАТИЧЕСКОГО АНАЛИЗА
Тема 3.2. Дифференциальное исчисление функции одной действительной переменной
Задание 14. Решение задач на нахождение производных высших порядков, раскрытие неопределенностей по правилу Лопиталя – 1 ч.
Цель: формирование умения находить производные высших порядков, вычислять пределы функций, раскрывая неопределенности по правилу Лопиталя.
Задание для самостоятельной внеаудиторной работы:
&14.1.Выучите определение производной n-го порядка. Проанализируйте, как найти производную второго, третьего и четвертого порядков.
?14.2. Найдите вторую производную функции:
а) 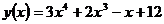 ; б)
; б) 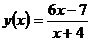 ; ¶в)
; ¶в) 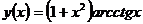 ; ¶г)
; ¶г) 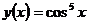 .
.
?14.3. Найдите третью производную функции:
а) 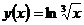 ; ¶б)
; ¶б) 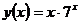 .
.
?14.4. Найдите четвертую производную функции 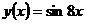 .
.
¶ 14.5. Выясните, сколько раз нужно продифференцировать функцию 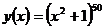 , чтобы в результате получился многочлен тридцатой степени.
, чтобы в результате получился многочлен тридцатой степени.
 &14.6.Запомните, в каких случаях используется правило Лопиталя. Выясните, как оно применяется.
&14.6.Запомните, в каких случаях используется правило Лопиталя. Выясните, как оно применяется.
i14.7. Установите правильную последовательность косточек математического домино и Вы узнаете титул французского математика Гийома Франсуа Антуана де Лопиталя (1661 – 1704):
· автора первого печатного учебника по дифференциальному исчислению;
· учёного, в честь которого назван приём раскрытия неопределённостей вида  или
или  .
.
| Р | 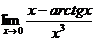 | И ∞ | 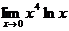 | 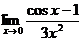 | З | 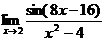 | ||||
A 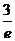 | 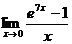 | K 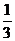 | 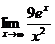 | M 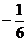 | 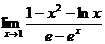 |
Методические указания по выполнению работы:
Для успешного решения задач необходимо знание следующего теоретического материала:

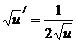 ·u'
·u'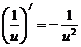 ·u'
·u'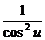 ·u'
·u'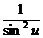 ·u'
·u' ·u'
·u'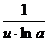 ·u'
·u'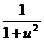 ·u'
·u'