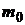Кредитный и заемный портфели

Критериальное множество

Пусть инвестор имеет возможность сформировать портфель, содержащий кроме чисто рисковых активов 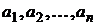и так называемый безрисковый актив 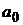, с параметрами 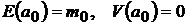. Тогда ковариационная матрица 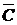будет вырожденной, имеющей нулевые первую строку и первый столбец.

,

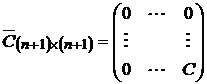где 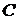– невырожденная ковариационная матрица для рисковых активов, а вектор доходностей – .

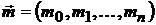Представим портфель 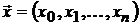в виде суммы двух портфелей (безрискового и чисто рискового ):

,

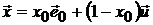где

.

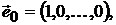
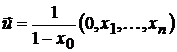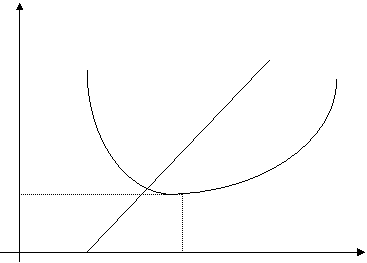
Построим на плоскости 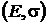критериальное множество для рисковых портфелей 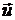и оценку 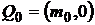безрискового портфеля .

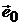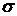
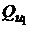
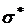
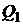
0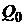

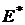
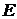
Рис.7.

Оценка 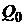лежит левее 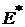, то есть 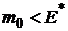, что естественно, так как в безрисковый актив должен иметь доходность ниже, чем «наилучший по риску» портфель, состоящий из рисковых активов.

Составим следующую линейную комбинацию рискового и безрискового портфелей:

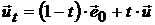, (26)

и вычислим его характеристики:

,

,

.

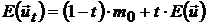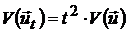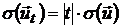Таким образом, риск портфеля, состоящего из безрискового актива 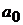и «рискового актива» 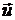, равен произведению риска «рискового актива» 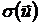на его удельный вес 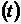в портфеле. Изменяя удельный вес актива , инвестор может построить портфель с различными характеристиками риска и доходности, все они располагаются на отрезках вида 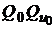и их риск пропорционален удельному весу 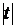рискованного актива. Такой портфель можно рассматривать как покупку инвестором рискового актива в сочетании с предоставлением кредита (покупка актива 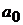), так как приобретение актива без риска есть не что иное, как кредитование эмитента. Поэтому портфели на отрезк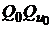е , где 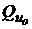лежит на минимальной границе рисковых портфелей, например, 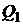называют кредитными.

Инвестор может построить свою стратегию не только на основе предоставления кредита, но и заимствуя средства под более низкий процент, чем ожидаемая доходность рискового актива 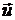, с целью приобретения на них активов 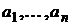, для получения дополнительного дохода. В этом случае 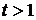, и инвестор может получить более высокий доход, чем 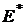, но с более высоким риском, чем 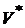, например, это портфель 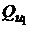. Поскольку для формирования такого портфеля инвестор занимает средства, то его еще называют заемным портфелем. Это портфели, оценки которых лежат, например, на луче 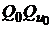«выше», чем .

Таким образом, на плоскости 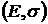оценки портфелей (26) будут лежать на лучах, соединяющих оценку 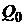безрискового портфеля 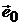с оценкой 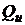рискового портфеля 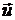. Меняя 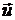, будем получать различные лучи, совокупность которых и составит критериальное множество для класса всех портфелей вида (26):

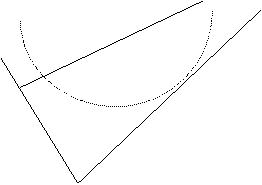
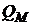
0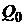

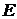
Рис.8.

Это множество представляет собой часть плоскости, ограниченной парой крайних лучей, выходящих из точки 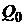. Правый луч будет касательным к гиперболе (минимальной границе критериального множества портфеля 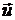), а левый луч будет параллелен левой асимптоте этой гиперболы. Оценка 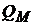- это точка касания граничного луча с гиперболой.

Для модели Марковица случай с безрисковым активом 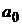рассматривается также, как и в модели Блека. И критериальное множество на плоскости 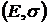будет иметь следующий вид.

Рис.9.