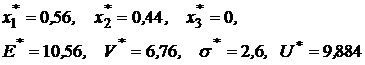Функция полезности инвестора.

Еще одним подходом к формированию оптимального портфеля является максимизация функции полезности. Функция полезности описывает правило, по которому каждому из возможных вариантов выбора приписывается некоторое числовое значение. Чем больше это значение, тем больше «полезность» данного варианта выбора. Другими словами, в теории портфеля функция полезности выражает предпочтения субъекта при определенных отношениях к риску и представлениях об ожидаемой доходности. То есть, это некоторый «суперкритерий», который представляет собой однозначную функцию от обоих критериев, рассмотренных выше, то есть

, или . (19)

Такая функция позволяет делать выбор в тех случаях, когда значения критериев и не позволяют этого сделать, например, при сравнении двух портфелей, оптимальных по Парето.

Для задачи выбора оптимального портфеля функция полезности обычно представляется в виде:

, (20)

где и величина характеризует склонность инвестора к риску, а именно, чем больше , тем более инвестор склонен к риску.

При нахождении мы «решаем» сразу две задачи: это и , что позволяет, как бы объединить проблему выбора портфеля с меньшим риском с выбором портфеля с большей эффективностью (доходностью).

В графической форме функцию полезности отражают кривые безразличия. На плоскости они представляют собой прямые линии, а на плоскости - параболы. Их можно задать уравнениями вида:

и , (21)

где 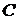- произвольная постоянная – « полезность» портфеля. Точки одной такой кривой определяют значения риска и доходности для данного уровня полезности .

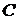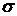
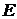
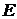
Рис.3.

Портфели и ( и ) – будут равносильными, или эквивалентными по инвестиционным качествам, так как лежат на одной кривой безразличия:

~ , ~ ,

а портфель ( ) будет предпочтительнее портфеля ( ), так как полезность этого портфеля больше соответствующий полезности :

.

Кроме того, крутизна линий безразличия характеризует склонность инвестора к риску. Чем эти линии «круче», тем инвестор более склонен к риску, так как он при небольшом увеличении доходности , согласен на большее увеличение риска.

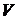
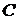
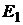
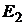
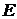
Рис.4.

Инвестор с линией безразличия более склонен к риску, чем инвестор с линией безразличия .

Выбор оптимального портфеля

Задача максимизации полезност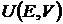и или 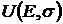формулируется следующим образом:

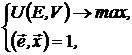(22)

для модели Блека, и добавлением неравенства 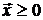для модели Марковица.

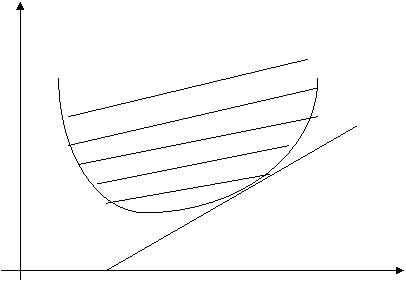
Геометрически решение такой задачи для модели Блека можно представить следующим образом ( 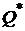- оптимальный портфель):

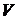
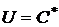
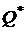
0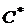

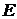
Рис.5.

То есть оптимальная линия уровня 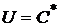является касательной к эффективной границе критериального множества.

Для модели Марковица возможны два варианта: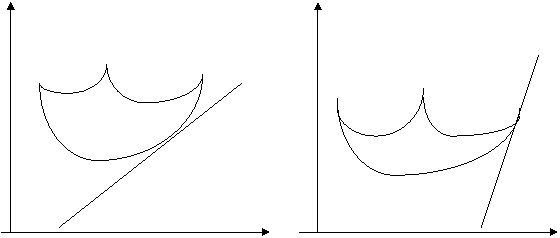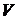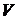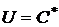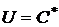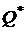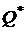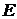

0 0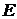

Рис.6.

Во втором случае оптимальная линия уровня 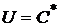не является касательной к эффективной границе, а имеет с ней общую верхнюю (угловую) точку .

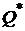Найдем аналитическое решение задачи (22) методом множителей Лагранжа, для чего составим функцию:

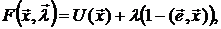
или

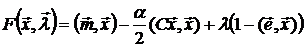. (23)

Вычислим ее частные производные первого порядка и приравняем их к нулю:

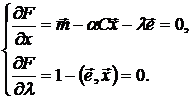
Выразим 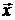из первого уравнения этой системы:

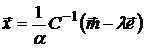
и подставим во второе уравнение

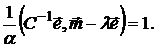
Откуда получаем

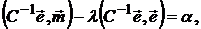
или

-

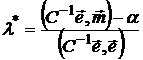оптимальное значение множителя Лагранжа.

Следовательно, оптимальный (с точки зрения полезности ) портфель будет иметь вид

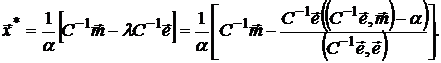(24)

Откуда легко вычислить как оптимальное значение полезности 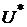, так и оптимальные характеристики портфеля 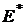и .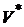

Если в (24) некоторые 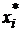будут отрицательными, то для модели Марковица поступаем так же, как и в предыдущих параграфах.

№ 12. В условиях № 7 найти портфель максимальной полезности при .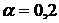

Решение. Составим функцию Лагранжа

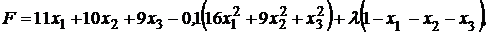
и получим систему уравнений:

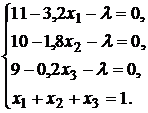
Выразив из первых трех уравнений

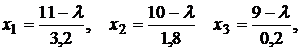
и подставив в четвертое уравнение

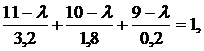
получим

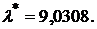
Следовательно, оптимальный портфель будет иметь структуру:

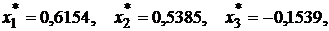
с доходностью

,

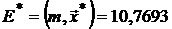риском

,

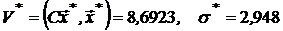и полезностью

.

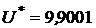Так как 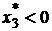, то оптимальное решение найдено для модели Блэка. Найдем оптимальное решение по Марковицу. Для этого примем 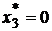и решим задачу снова, с функцией Лагранжа:

.

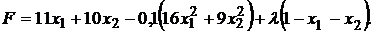Тогда

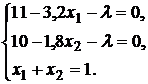
Решив эту систему, получим портфель, оптимальный по Марковицу:

.

.

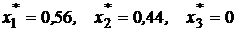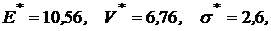
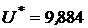Если портфель содержит безрисковый актив , то для построения оптимального портфеля строим следующую функцию Лагранжа

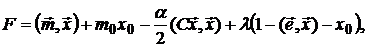
что приводит к системе уравнений

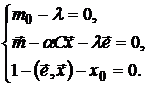(25)

Подставив 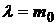во второе уравнение, получаем следующую структуру оптимального портфеля

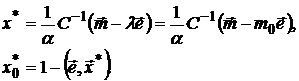
№ 13. Решите № 12 при условии, что актив 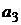- безрисковый.

Решение. Составив функцию Лагранжа:

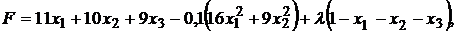
получаем систему уравнений

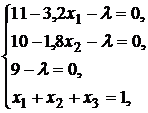
решение которой имеет вид:

,

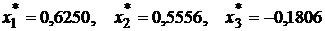с доходностью

,

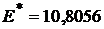риском

,

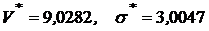и полезностью

.

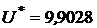Так как 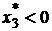, то это решение - оптимальное в модели Блека. Найдем решение оптимальное по Марковицу, для чего примем 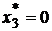. Тогда

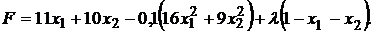
и

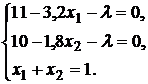
Решив эту систему, получаем: