Функция распределения вероятностей и плотность вероятности
Непрерывные случайные величины характеризуются тем, что их значения могут сколь угодно мало отличаться друг от друга.
Вероятность события X < х (где X – значение непрерывной случайной величины, а х – произвольно задаваемое значение), рассматриваемая как функция от х, называется функцией распределения вероятностей:
F(x) = Р(Х <х).
Производная от функции распределения вероятностей называется функцией плотности распределения вероятностей или плотностью вероятности:
f(x) = F'(x).
Функция распределения вероятностей выражается через плотность вероятности в виде интеграла:
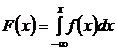 .
.
Вероятность попадания случайной величины в интервал (х1, х2) равна приращению функции распределения вероятностей на этом интервале:
P(x1<X<x2) = F(x2) – F(x1). (4)
3.1. Случайная величина X задана функцией распределения вероятностей:
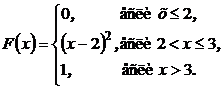
Найти плотность вероятности f(x) и вероятность попадания случайной величины X в интервалы (1; 2,5), (2,5; 3,5).
Решение. Плотность вероятности находим по формуле f(x) = F'(x):
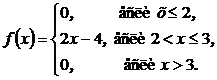
Вероятности попадания случайной величины X в интервалы вычисляем по формуле (3.1):
Р(1 < X < 2,5) = F(2,5) – F(1) = 0,52 – 0 = 0,25;
Р(2,5 < X < 3,5) = F(3,5) – F(2,5) = 1 – 0,25= 0,75.
3.2. Плотность вероятности непрерывной случайной величины X:
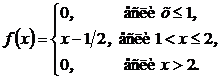
Найти функцию распределения F(х) и построить ее график.
Решение.
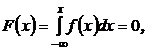 если
если 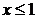 ,
,
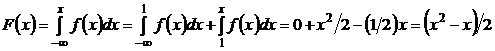 ,
,
если 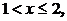
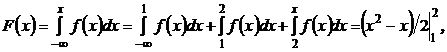 если х > 2.
если х > 2.
График функции представлен на рис. 3.1.
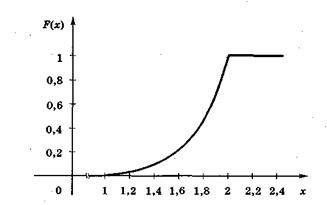
Рис. 3.1
3.3. Плотность вероятности непрерывной случайной величины X задана в виде 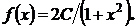
Найти параметр С.
Решение. На основании равенства
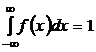
имеем:
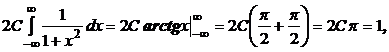
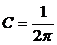 .
.
Математическое ожидание и дисперсия. Мода и медиана
Средним значением или математическим ожиданием непрерывной случайной величины X называется значение интеграла
М(Х) = Мх = 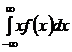 ,
,
где f(x) – плотность вероятности.
Дисперсией непрерывной случайной величины X называется значение интеграла
D(X) = Dx= 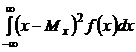 .
.
Для определения дисперсии может быть также использована формула
Dx= 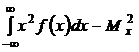 .
.
Модой М0(Х) непрерывной случайной величины X называется такое значение этой величины, плотность вероятности которого максимальна.
Медианой Мe(Х) непрерывной случайной величины X называется такое ее значение, при котором выполняется равенство
Р(Х < Me) = Р(Х > Me).
3.4. Случайная величина X задана плотностью вероятности f(x) = х/2 в интервале (0; 2), вне этого интервала f(x) = 0. Найти математическое ожидание величины X.
Решение. На основании формулы
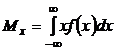
имеем:
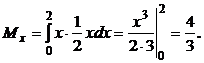
3.5. Случайная величина X задана плотностью вероятности f(x) = x/8 в интервале (0; 4). Вне этого интервала f(x) = 0. Найти математическое ожидание.
3.6. Случайная величина X задана плотностью вероятности f(x) = 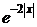 при
при 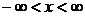 . Найти математическое ожидание.
. Найти математическое ожидание.
3.7. Случайная величина X задана плотностью вероятности f(x) = С(х2 + 2х) в интервале (0; 1). Вне этого интервала f(x) = 0. Найти параметр С.
Решение. Так как
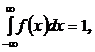 то:
то:
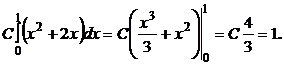
Откуда С = 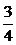 .
.
Равномерное распределение
Непрерывная случайная величина называется равномерно распределенной на отрезке [а, b], если ее плотность вероятности имеет вид:
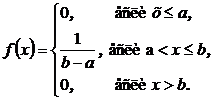
Математическое ожидание и дисперсия равномерно распределенной случайной величины определяются выражениями
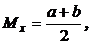
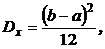
3.8. Случайная величина X распределена равномерно на отрезке [1; 6]. Найти функцию распределения F(x), математическое ожидание, дисперсию и среднее квадратичное отклонение величины.
Решение. Плотность вероятности для величины X имеет вид:

Следовательно, функция распределения, вычисляемая по формуле:
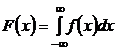 ,
,
запишется следующим образом:
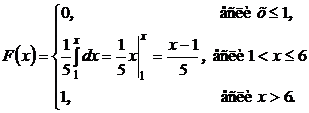
Математическое ожидание будет равно Мх = (1 + 6)/2 = 3,5. Находим дисперсию и среднее квадратичное отклонение:
Dx = (6 – 1)2/12 = 25/12, 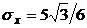 .
.
Нормальное распределение
Случайная величина X распределена по нормальному закону, если ее функция плотности распределения вероятностей имеет вид:
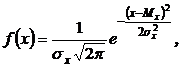
где Мх – математическое ожидание;
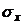 – среднее квадратичное отклонение.
– среднее квадратичное отклонение.
Вероятность попадания случайной величины в интервал (а, b) находится по формуле
Р(а < X < b) = Ф 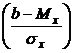 – Ф
– Ф 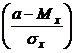 = Ф(z2) – Ф(z1), (5)
= Ф(z2) – Ф(z1), (5)
где Ф(z) = 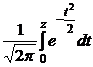 – функция Лапласа.
– функция Лапласа.
Значения функции Лапласа для различных значений z приведены в Приложении 2.
3.9. Математическое ожидание нормально распределенной случайной величины X равно Мх = 5, дисперсия равна Dx = 9. Написать выражение для плотности вероятности.
3.10. Математическое ожидание и среднее квадратичное отклонение нормально распределенной случайной величины X соответственно равны 12 и 2. Найти вероятность того, что случайная величина примет значение, заключенное в интервале (14; 16).
Решение. Используем формулу (21.2), учитывая, что Мх = 12, 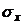 = 2:
= 2:
Р(14 < X < 16) = Ф((16 – 12)/2) – Ф(14 – 12)/2) = Ф(2) – Ф(1).
По таблице значений функции Лапласа находим Ф(1) = 0,3413, Ф(2) = 0,4772. После подстановки получаем значение искомой вероятности:
Р(14 <Х < 16) = 0,1359.
3.11. Имеется случайная величина X, распределенная по нормальному закону, математическое ожидание которой равно 20, среднее квадратичное отклонение равно 3. Найти симметричный относительно математического ожидания интервал, в который с вероятностью р = 0,9972 попадет случайная величина.
Решение. Так как Р(х1 < Х < х2) = р = 2Ф((х2 – Мх)/ 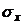 ), то Ф(z) = р/2 = 0,4986. По таблице функции Лапласа находим значение z, соответствующее полученному значению функции Ф(z) = 0,4986: z = 2,98. Учитывая то, что z = (х2 – Мх)/
), то Ф(z) = р/2 = 0,4986. По таблице функции Лапласа находим значение z, соответствующее полученному значению функции Ф(z) = 0,4986: z = 2,98. Учитывая то, что z = (х2 – Мх)/ 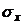 , определяем
, определяем 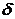 = х2 – Мх =
= х2 – Мх = 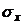 z = 3 · 2,98 = 8,94. Искомый интервал будет иметь вид (11,06; 28,94).
z = 3 · 2,98 = 8,94. Искомый интервал будет иметь вид (11,06; 28,94).
Показательное распределение
Распределение непрерывной случайной величины X называется показательным (экспоненциальным), если плотность вероятности этой величины описывается функцией:
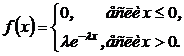
где 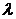 – положительное число.
– положительное число.
Соответственно, функция распределения вероятностей имеет вид:
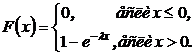
 3.12. Случайная величина X задана функцией распределения вероятностей
3.12. Случайная величина X задана функцией распределения вероятностей
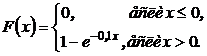
Найти математическое ожидание и дисперсию величины X.
Решение. Для решения задачи используем формулы математического ожидания и дисперсии непрерывной случайной величины:
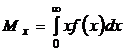 ,
, 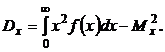
Учтем, что f(x) = F'(x). Тогда получим:
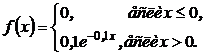
Подставим в выражение для математического ожидания
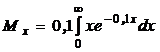 .
.
Интегрируя по частям, получаем Мх = 1/ 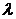 , или Мх = 1/0,1.
, или Мх = 1/0,1.
Для определения дисперсии проинтегрируем по частям первое слагаемое. В результате получим:
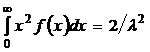 .
.
Учтем найденное выражение для Мх. Откуда
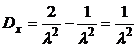 .
.
В данном случае Мх = 10, Dx = 100.
СИСТЕМЫ СЛУЧАЙНЫХ ВЕЛИЧИН
