Глава 6. Неопределенный интеграл

Глава 6. Неопределенный интеграл

Первообразная

Определение 1.Функция 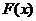называется первообразной функции 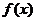, если .

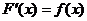Пример.

Рассматриваемый ниже пример очень важен для дальнейшего. Пусть 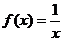. Утверждается, что в этом случае первообразная .

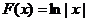Проверяем:

Пусть 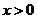. Тогда 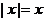и .

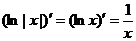Пусть теперь 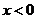. Тогда 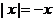и ,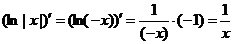

так что всегда .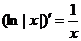

Теорема. Есл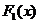и и 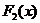- две первообразные от одной и той же функции 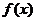, то .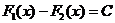

Доказательство.

Действительно, в этом случае 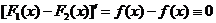и поэтому, согласно условия постоянства функции, .<

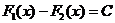Следствие. Если 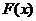есть одна из первообразных функции 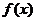, то любая другая первообразная имеет вид .

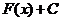Определение 2. Совокупность всех первообразных функции 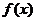называется неопределенным интеграломот 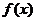и обозначается .

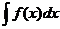Таким образом

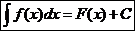
где 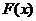есть любая из первообразных функции .

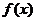Термины.

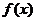- подынтегральная функция;

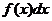- подынтегральное выражение.

Свойства неопределенного интеграла

1. .

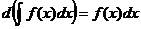Действительно, если 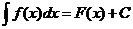, то .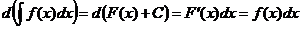

2.

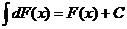
Действительно, .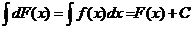

Подытоживая эти два свойства можно сказать, что стоящие рядом знаки d и взаимно уничтожаются, то есть операция дифференцирования и операция интегрирования есть взаимно обратные операции.

3. .

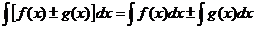Действительно, пусть и 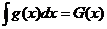. Но тогда

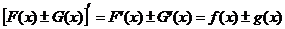
и поэтому

.

4. .

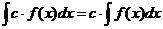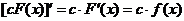Действительно, пусть . Но тогда и поэтому

.

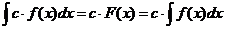Таблица неопределенных интегралов

Ниже приводится таблица неопределенных интегралов которая, по сути дела, является переписанной «наоборот» таблицей производных.

1.	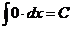6.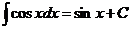
2. 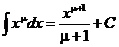,	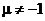7.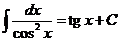
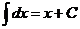	8.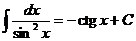
3.	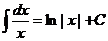9.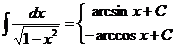
4.	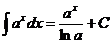10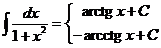
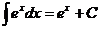	11.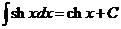
5.	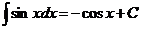12.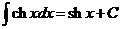

Эту таблицу следует зазубрить.

Основные приемы интегрирования

В отличие от проблемы вычисления производных, где жесткие формальные правила позволяют, в принципе, вычислить производную от любой элементарной функции, в проблеме вычисления интегралов таких жестких формальных правил нет. Есть только некоторые приемы, но успех их применения очень сильно зависит от опыта и интуиции. Дело осложняется тем, что имеется огромное количество так называемых «неберущихся» интегралов, то есть таких интегралов, которые не выражаются через элементарные функции и носят название элементарных функций.

Тем не менее, укажем два основных приема.

Замена переменных

Пусть надо вычислить 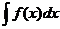. Перейдем от переменной х к переменной t по формуле 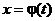, так что 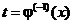. Тогда 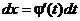и мы получаем

.

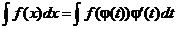Пусть нам каким-то способом удалось вычислить последний интеграл и он оказался равен 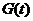, то есть . Тогда утверждается, что

.

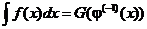Докажем это. Итак

1. . Это значит, что .

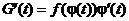2. Найдем производную от 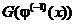. Вспоминая формулу производной от сложной функции, а затем формулу производной от обратной функции, получим

,

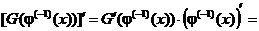
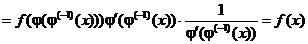так как сомножители 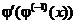сокращаются, а 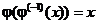. Следовательно, . <

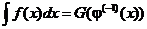Эта формула является основным методом вычисления неопределенных интегралов. Ее пишут в виде цепочки

.

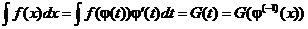Обратите внимание на основные этапы работы.

1. Вводим 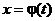(как Вы его введете - это Ваше дело).

2. Находим заранее .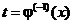

3. Вычисляем интеграл (как Вы это сделаете - Ваши проблемы).

4. Возвращаемся к исходному интегралу .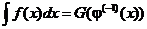

Как Вы видите - рекомендации достаточно общие.

Интегрирование по частям

Пусть даны две дифференцируемые функци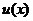и и 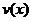. Тогда, по свойствам дифференциалов,

.

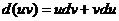Интегрируя это соотношение, получим 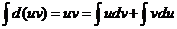. Отсюда следует, что

.

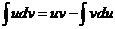Эта формула и носит название формулы интегрирования по частям.

Пример.

Пусть надо вычислить интеграл .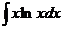

Разбиваем подынтегральное выражение на кусочки 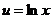, 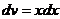. Отсюда получается, что 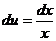, 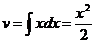. Формула интегрирования по частям дает тогда

.

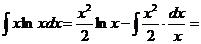
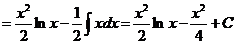Как уже говорилось выше, четких и однозначных алгоритмов вычисления неопределенных интегралов нет и не может быть, так как имеется огромное число так называемых неберущихся интегралов, то есть таких интегралов, которые не выражаются через элементарные функции и представляют собой класс так называемых специальных функций. Однако имеются определенные классы функций, для которых алгоритмы вычисления интегралов могут быть четко сформулированы. К изучению этих классов функций мы и переходим. Но, прежде чем приступить к их изучению, придется сделать небольшое, но очень важное отступление.

6.5 Комплéксные числа

В математике большую роль играют так называемые обратные операции, необходимость выполнения которых обычно приводит к расширению классов имеющихся математических объектов.

Например, операция сложения. Когда-то люди не знали отрицательных чисел. Складывая положительные числа, в ответе всегда получаем положительное число. Но обратная операция - вычитание - привела к необходимости рассматривать числа отрицательные.

Операция умножения. Перемножая целые числа, в ответе всегда получаем также целое число. Обратная операция - деление - приводит нас к необходимости рассматривать дробные, рациональные числа.

Операция возведения в квадрат. Квадрат рационального числа есть всегда также число рациональное. Но обратная операция - извлечение квадратного корня - приводит к иррациональным числам ( 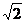, например), то есть к числам, не являющимся рациональными.

Но та же операция извлечения квадратного корня дает и еще один класс чисел. Как известно, квадрат любого числа есть число неотрицательное. Поэтому и квадратный корень можно извлекать только из неотрицательных чисел (например, 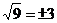). А как быть с 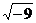? Чему он равен? Ведь нет такого вещественного числа, квадрат которого был бы равен - 9.

Но, как говорится, если нельзя, но очень хочется - то можно. И желание извлекать квадратные корни из отрицательных чисел привело к новому классу чисел, называемых комплéксными числами. Для их рассмотрения оказалось достаточным ввести всего лишь одно новое число

,

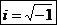которое называется «мнимой единицей». Считается, что это «число» обладает всеми свойствами обычных чисел, и имеет всего одно единственное новое свойство

.

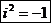Так что, например, 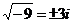, ибо 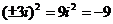. Числа, содержащие i, называются комплéксными числами. Без них немыслима современная математика.

Корни полинома

Определение.Число b (действительное или комплексное) называется корнемполинома 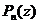, если .

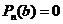Теорема 1. Для того, чтобы b было корнем полинома 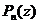,необходимо и достаточно, чтобы 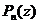делилось на .

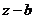Доказательство.

По сказанному выше, имеем

,

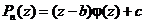где с - полином степени 0, то есть константа. Тогда

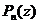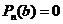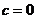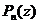1. Если b есть корень , то , откуда следует, что и делится на .

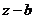2. Если 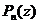делится на 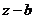, то 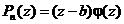и тогда 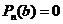, то есть b корень полинома . <

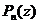Теорема 2. Пусть корень полинома b есть комплексное число. Тогда комплексно сопряженное число 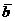также является корнем этого полинома.

Доказательство.

1. Докажем сначала, что 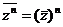. Имеем

,

,

.

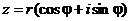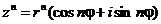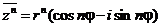С другой стороны

,

.

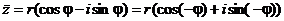2. Так как по условию все коэффициенты полинома есть действительные числа, то .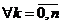

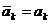3. Поэтому, если

,

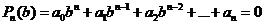то

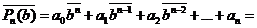
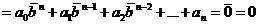
и 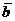также есть корень полинома . <

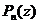Таким образом, комплексные корни полинома всегда «ходят парами»: если 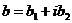есть корень, то 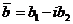- тоже корень.

Основная теорема алгебры. Всякий полином степени п ³ 1 имеет хотя бы один корень (действительный или комплексный).

Доказывать эту теорему мы не будем - все-таки это курс математического анализа, а не алгебры.

Теорема 3. Полином степени п имеет ровно п корней.

Доказательство.

Рассмотрим полином 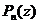. Тогда, по основной теореме алгебры, 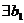такое, что 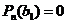и поэтому имеет место разложение .

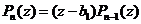Рассмотрим полином 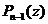. Тогда, по основной теореме алгебры, 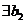такое, что 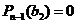и поэтому имеет место разложение .

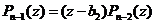Рассмотрим полином 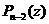. Тогда, по основной теореме алгебры, 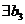такое, что 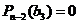и поэтому имеет место разложение .

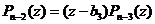И т.д., и т.д., и т.д.

Заметим, что каждый раз степень полинома уменьшается на 1. В конце концов, на п-м шаге мы дойдем до полинома степени 0 и получим такое разложение

.

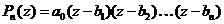Других корней у этого полинома нет, так если z не совпадает с каким-то из 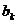, то все сомножители вида 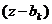отличны от нуля и . <

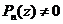Определение.Если в разложении 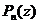на сомножители бином 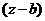повторяется k раз, то говорят, что корень b имеет кратность k.

Если k = 1, то корень называется простым.

Заметим еще, что в паре комплексно сопряженных корней оба корня имеют одинаковую кратность.

Общий вид разложения.

Пусть 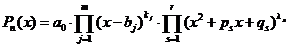и 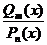есть правильная рациональная дробь. Тогда имеет место разложение

.

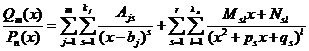Это представление называется разложением правильной рациональной дроби на простейшие.

Заметим в заключение, что некоторыеиз коэффициентов 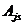, 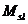и 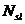могут бытьравны нулю.

Метод вычеркивания

Вспомним еще раз терему 1. Там было

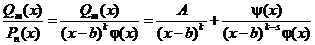
и, в частности, была явная формула для коэффициента А:

.

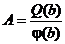Именно эта формула и дала название «метод вычеркивания». Ее формулируют обычно так: чтобы найти коэффициент при 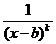надо в исходном выражении вычеркнуть в знаменателе сомножитель 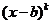и в оставшемся выражении заменить х на b.

Пример.

Разложить на простейшие

.

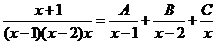Согласно сформулированному правилу имеем

;

;

,

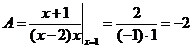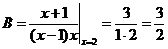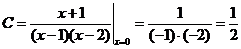так что

.

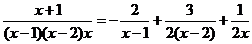Однако отметим, что так можно находить не все коэффициенты, а лишь коэффициенты при старших степенях вещественных корней.

Комбинирование

Рекомендуется комбинировать метод вычеркивания и метод неопределенных коэффициентов и часть коэффициентов методом вычеркивания, а оставшиеся - методом неопределенных коэффициентов.

Рассмотрим это на том примере, который мы рассматривали в методе неопределенных коэффициентов:

.

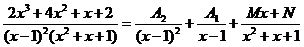Здесь коэффициент 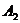можно найти методом вычеркивания

.

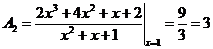Оставшиеся коэффициенты надо находить методом неопределенных коэффициентов. Знание 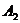приведет к тому, что нам надо будет решать систему только из трех уравнений, а не четырех, причем из получающейся системы четырех уравнений мы можем выбрать любые три по нашему вкусу.

Универсальная подстановка

Эта подстановка имеет вид .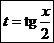

Докажем, что она приводит рассматриваемый класс интегралов к интегралам от дробно рациональных функций. Имеем:

;

;

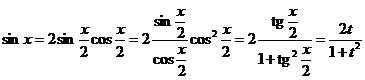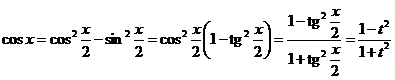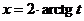Þ .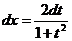

В результате рассматриваемый интеграл принимает вид

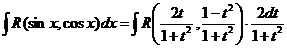
и он является интегралом от дробно рациональной функции, который вычисляется при помощи разложения на простейшие.

Упрощенные подстановки

Универсальная подстановка потому и называется универсальной, что позволяет любыеинтегралы рассматриваемого типа сводить к интегралам от дробно рациональных функций. Однако, получающиеся при этом интегралы обычно достаточно сложны. Поэтому ее следует использовать только в том случае, если нельзя применить так называемые упрощенные подстановки, к рассмотрению которых мы и переходим. Их всего три.

1. Условие применимости первой упрошенной подстановки имеет вид

.

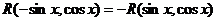Чтобы изложение дальнейшего было короче, будем писать u вместо 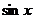и v вместо 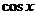. Тогда условие применимости первой упрощенной подстановки примет вид .

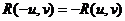Но в нашей формуле, определяющей функцию 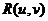и в числителе и в знаменателе стоят полиномы по переменным и и v. Когда же функция 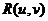будет нечетной функцией по переменной и? Легко догадаться, что это будет тогда, когда сомножитель и можно вынести за скобки и, после этого, в числителе и знаменателе останутся лишь полиномы от переменной и², то есть тогда, когда функция 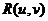может быть приведена к виду .

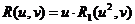Это условие и определяет первую упрощенную подстановку. Она имеет вид

.

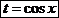Тогда 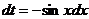и мы имеем

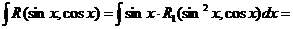
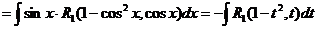
и мы получили интеграл от дробно рациональной функции.

2. Условие применимости второй упрошенной подстановки имеет вид

.

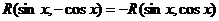Повторяя почти дословно все рассуждения, касающиеся первой упрощенной подстановки, можно получить, что в этом случае функция 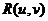может быть приведена к виду .

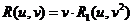Вторая упрощенная подстановка имеет вид 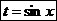. Тогда 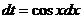и мы имеем

=

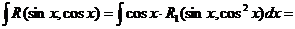
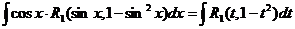
и мы получили интеграл от дробно рациональной функции.

2. Условие применимости третьей упрошенной подстановки имеет вид

.

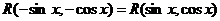Попытаемся сообразить, что это дает относительно вида функции 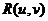. Прежде всего имеем

.

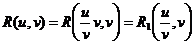Тогда условие применимости третьей упрощенной подстановки дает

.

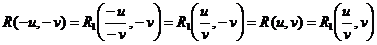Используя те же рассуждения, что и выше, легко догадаться, что второй аргумент у 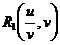должен содержать только четныестепени v. Поэтому 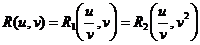, и

.

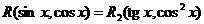Это и определяет третью упрощенную подстановку. Она имеет вид 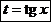. Действительно, в этом случае

, , ,

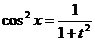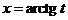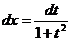и наш интеграл принимает вид

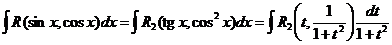
и мы получили интеграл от дробно рациональной функции.

6.11 Вычисление интегралов вида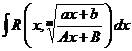

Рассмотрим вычисление интегралов вида 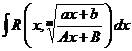при условии 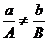(очевидно, что если имеет место равенство, то под знаком корня дробь сократится, и будет просто интеграл от дробно рациональной функции).

Все, что здесь надо запомнить - это то, какую замену переменных (подстановку) здесь нужно сделать, а именно

.

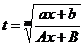Дальше все идет само собой. Выражаем х через t

, , ,

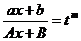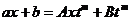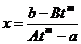и самое неприятное - корень - исчез.

Далее имеем

.

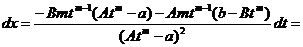
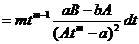Заметим, что .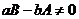

Окончательно получаем

,

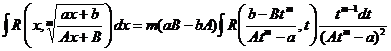и мы получили интеграл от дробно рациональной функции.

6.12 Вычисление интегралов вида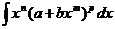

Рассмотрим теперь вычисление интегралов вида 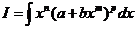,где т, п, и р - рациональныечисла.

Рассмотрим четыре возможных случая.

1. р - целое положительноечисло.

Тогда следует комбинацию 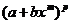раскрыть по формуле бинома Ньютона, раскрыть скобки и проинтегрировать почленно.

2. р - целое отрицательноечисло.

Вспомним, что т и п - рациональныечисла. Это значит, что они представимы в виде 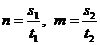. Пусть r есть наименьшее общее кратноечисел t₁ и t₂. Тогда .

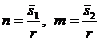Теперь сделаем замену переменных 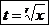. Тогда получаем

, , ,

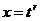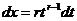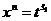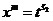
и рассматриваемый интеграл принимает вид

,

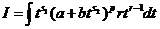и степени у t всюду целые числа и мы получили интеграл от дробно рациональной функции.

3. Комбинация 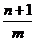- целое число.

Пусть 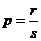. Тогда надо сделать следующую замену переменных

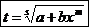
(обратите внимание, откуда в показателе корня взялось это s!).

А теперь проделаем аккуратно все выкладки. Сначала выразим х через t:

; .

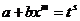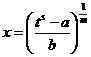Теперь найдем dx

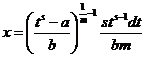
и подставим все это в изучаемый интеграл

.

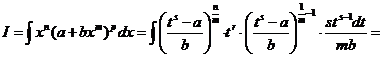
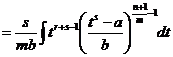Но 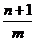- целое число! Все остальные степени также целые числа. Поэтому под знаком интеграла стоит дробно рациональная функция и интеграл вычисляется методом разложения подынтегральной функции на простейшие.

4. Комбинация 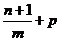- целое число.

Пусть снова 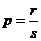. Тогда надо сделать следующую замену переменных

.

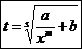А теперь проделаем аккуратно все выкладки. Сначала выразим х через t:

; .

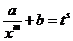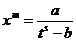Дифференцируем последнее соотношение

.

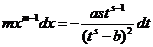Попытаемся переписать подынтегральное выражение так, чтобы в нем была явно видны комбинации, равные 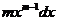и t:

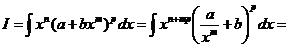
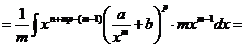
Заметим теперь, что

,

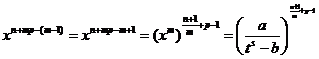так что, продолжая предыдущую строку, получаем

.

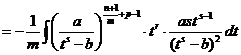Но 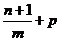- целое число. Все остальные степени также целые числа. Поэтому под знаком интеграла стоит дробно рациональная функция и интеграл вычисляется методом разложения подынтегральной функции на простейшие.

Как показал знаменитый русский математик П.Л. Чебышёв, во всех остальных случаях рассматриваемый интеграл через элементарные функции не выражается.

6.13 Вычисление интегралов вида 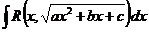. Подстановки Эйлера

Рассмотрим теперь вычисление интегралов вида 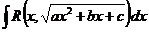.Они находятся с помощью так называемых подстановок Эйлера. Вообще-то их три, но мы рассмотрим только две - первую и третью.

Первая подстановка Эйлера

Эту подстановку можно применять, если выполнено условие 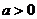. Она имеет вид

.

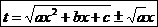Проделаем все вычисления, взяв, для определенности, знак +. Тогда

.

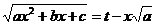Возводим это выражение в квадрат

,

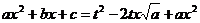сокращаем 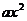и выражаем в явном виде х через t:

.

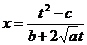Теперь можно выразить через t и комбинацию 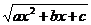. Имеем

,

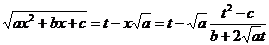и корень исчезает. Далее,

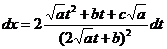
и подстановка всего этого в исходный интеграл приводит его к виду

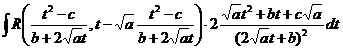
и под знаком интеграла стоит дробно рациональная функция от переменной t.

Третья подстановка Эйлера.

Условие применимости этой подстановки: полином 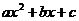имеет действительные корних₁ и х₂.

Сама третья подстановка Эйлера имеет вид

.

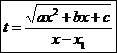Покажем, что она сводит наш интеграл к интегралу от дробно рациональной функции. Так как 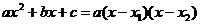, то

.

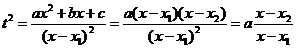Отсюда находится х через t:

.

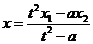Для комбинации 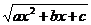получаем

,

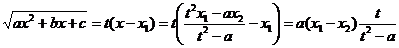и корень исчезает. Легко получить, что

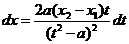
и рассматриваемый интеграл приводится к виду

,

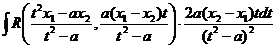и под знаком интеграла снова получилась дробно рациональная функция от переменной t.

Как видно из приведенных ниже рисунков, эти две подстановки исчерпывают все возможные случаи.

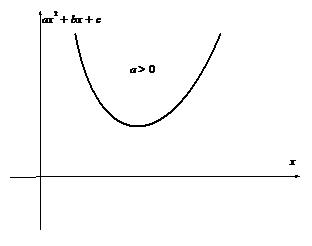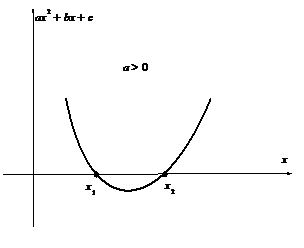Применима первая подстановка Эйлера	Применимы первая и третья подстановки Эйлера

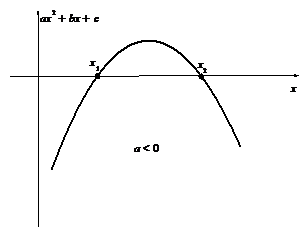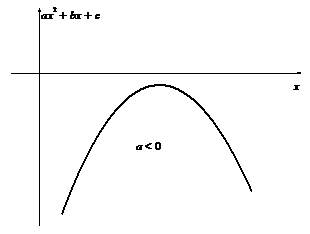Применима третья подстановка Эйлера	Подкоренное выражение всегда отрицательно, поэтому интеграл не имеет смысла.

Заметим в заключение, что если 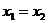, то 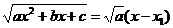и никаких иррациональностей нет.

Глава 6. Неопределенный интеграл

Первообразная

Определение 1.Функция 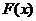называется первообразной функции 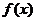, если .

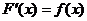Пример.

Рассматриваемый ниже пример очень важен для дальнейшего. Пусть 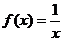. Утверждается, что в этом случае первообразная .

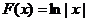Проверяем:

Пусть 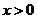. Тогда 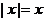и .

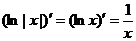Пусть теперь 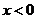. Тогда 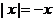и ,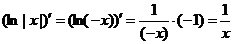

так что всегда .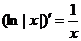

Теорема. Есл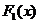и и 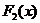- две первообразные от одной и той же функции 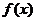, то .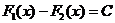

Доказательство.

Действительно, в этом случае 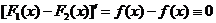и поэтому, согласно условия постоянства функции, .<

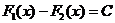Следствие. Если 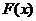есть одна из первообразных функции 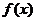, то любая другая первообразная имеет вид .

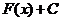Определение 2. Совокупность всех первообразных функции 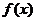называется неопределенным интеграломот 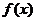и обозначается .

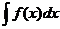Таким образом

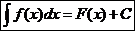
где 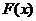есть любая из первообразных функции .

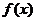Термины.

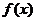- подынтегральная функция;

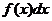- подынтегральное выражение.