Приближение вещественных чисел рациональными.

Как уже сказано выше, рациональных чисел счетное множество, а вещественных – континуум, то есть гораздо больше. Но есть некоторые свойства рациональных чисел, которые позволяют заменять вещественные числа рациональными.

Теорема 1. Для любого вещественного числа а и для любого 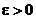найдутся два рациональных числа r₁ и r₂, такие, что:

а) 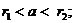б) .

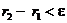(Обратите внимание, как может быть записана формулировка этой теоремы:

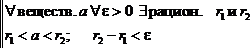
Правда, короче?)

Доказательство.

Возьмем любое 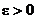. Так как по смыслу 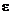мало, то пусть оно имеет вид: 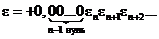Рассмотрим число 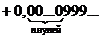, равное, очевидно 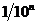. Пусть а>0. Распишем его:

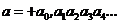
Предположим, что n–ая цифра после запятой 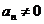. Рассмотрим числа

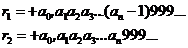
Тогда можно сказать, что

а) r₁ и r₂ - рациональные числа, так как у обоих из них бесконечные «хвосты» из девяток;

б) 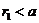, так как ;

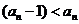в) 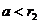, так как у r₂ после a_n все девятки, а у числа а хотя бы одна цифра не будет девяткой.

г) 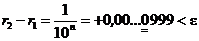, так как у e на n-м месте стоит e_n, а у разности 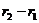на n-ом месте стоит .

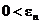Тем самым, построенные числа r₁ и r₂ удовлетворяют всем условиям теоремы. <

Подумайте сами, что надо изменить в доказательстве, если окажется, что .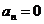

Теорема 2. Для любых двух вещественных чисел a и b, не равных друг другу, найдется такое рациональное число r, которое будет расположено между ними.

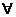( веществ. а, b а ≠ b 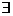рацион. r a<r<b)

Доказательство.

1. Пусть для определенности а<b и а>0. Тогда числа а и b имеют вид:

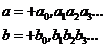
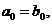
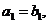
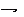
Так как а<b, то найдется такая цифра с номером n, чт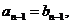о но 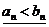(то есть ).

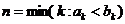В числе b после n-й цифры могут быть нули, но бесконечного «хвоста» из нулей быть не может, это запрещено. Поэтому b обязано иметь вид

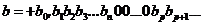
где b_p – первая цифра после следующей за b_n серии нулей, такая, что 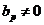(то есть ).

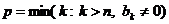Возьмем r в виде

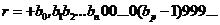
Тогда ясно, что

а) r – рациональное число, так как у него бесконечный «хвост» из девяток;

б) а < r, так как а_n < b_n.

в) r < b, т.к. (b_p-1) < b_p.

Построение r удовлетворяет всем требованиям нашей теоремы.

2. Пусть теперь а<0 и b>0. Тогда можно взять r = 0.

3. Пусть, наконец, a<0, b<0 и b < a. Тогда |a| < |b| и, согласно п.1, найдется такое рациональное число r, что |a| < r< |b|. Но тогда b < -r < a. Теорема доказана.<

Указанные две теоремы образуют то, что математики называют «плотностью» рациональных чисел относительно множества вещественных чисел. Это свойство плотности играет важную роль в доказательстве целого ряда теорем.

Терминология. Неравенства.

В заключение этого раздела уточним еще раз некоторые термины.

Множество чисел х, удовлетворяющее свойству a£x£ b, называется замкнутым отрезком и обозначается [a, b].

Множество чисел х, удовлетворяющее свойству a<x<b, называется открытым отрезком и обозначается (a, b).

Множество чисел х, удовлетворяющее свойству a<x£ b (или a£ x<b), называется полуоткрытым отрезком и обозначается (a, b] (соответственно [a, b)).

Модулем |x| числа х называется это же число, взятое со знаком «+». Очевидно, что всегда

-| x | £ x £ | x |

Важнейшее в дальнейшем для нас неравенство выглядит так: | x + y | £ | x | + | y |. Докажем его.

Имеем: -| x | £ x £ | x |; -| y | £ y £ | y |.

Складывая эти неравенства получим:

- (| x | + | y |) £ x + y £ | x | + | y |,

откуда и следует, что | x + y | £ | x | + | y | <

Отметим еще, что | x – y | £ | x | + | y |. Попытка записать это неравенство в виде

| x – y | £ | x | - | y | является грубейшей ошибкой. Никогда не допускайте ее!

Отметим еще, что неравенство 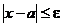эквивалентно такой цепочке:

.

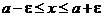Действительно, из 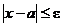следует, что 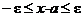, так как 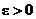и 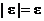. Прибавляя ко всем частям этой цепочки неравенств число а, получим .

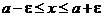Итак, запомните эквивалентную запись:

.

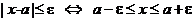Она будет основной в следующем разделе.

Открытый промежуток 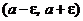называют «e-окрестностью» числа а (или «e-окрест­ностью» точки а).