ГЛАВА 1. Множества. Вещественные числа

ГЛАВА 1. Множества. Вещественные числа

Множества

Понятие множества является первоначальным математическим понятием, то есть таким понятием, которое можно только показать на примерах. Можно говорить, например, о множестве людей, находящихся в данной аудитории, о множестве четных чисел, о множестве точек отрезка и т.п. Множества мы будем в дальнейшем обозначать большими латинскими буквами, например, A, B, C и т.д. Иногда множества будут задаваться просто перечислением их элементов и для этого будет использоваться запись вида A={a}, где в {…} будут перечисляться элементы множества A. Например, A={a, b, c} есть множество, состоящее из элементов a, b и c.

Обозначение aÎA означает, что элемент a принадлежит множеству A, а обозначение 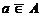или aÏA означает, что элемент a не принадлежит множеству A. Знаком Æ будет обозначаться так называемое пустое множество, то есть такое множество, в котором нет ни одного элемента.

Операции над множествами

1. Вхождение или включение множеств.

Говорят, что множество А входит во множество В (обозначение АÌВ) или множество В включает множество А (обозначение ВÉА) если из того, что некоторый элемент aÎA следует, что aÎВ (запись ).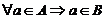

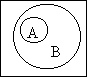Эту операцию можно пояснить следующим рисунком. Из него видно, что если АÌВ, то множество В шире множества А, то есть содержит бóльшее число элементов.

Если одновременно АÌВ и ВÌА, то означает, что множества А и В совпадают, или равны друг другу (обозначение А=В).

2. Объединение или сумма множеств.

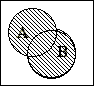Множество С называют объединением или сумой множеств А и В (обозначение С=АÈВ) если оно состоит из элементов, принадлежащих хотя бы одному из множеств А и В, то есть aÎС означает, что aÎA, или aÎВ или aÎи А и В одновременно. Это можно записать так: 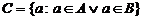, где знак Ú есть символ логического сложения (читается «или»). Эта операция может быть пояснена следующим рисунком.

Операция È обладает обычными свойствами:

1) АÈВ= ВÈА;

2) АÈ( ВÈС)=(АÈВ) ÈС.

Для суммы множеств А₁, А₂,…, А_n используют обозначение .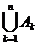

3. Пересечение или произведение множеств.

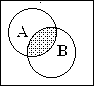Множество С называется пересечением или произведением множеств А и В (обозначается С=АÇВ) если оно состоит из элементов, принадлежащих одновременно и множеству А и множеству В. Это можно записать так: 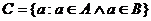где знак Ù есть символ логического умножения (читается «и»). Эта операция может быть пояснена следующим рисунком.

Операция Ç обладает свойствами:

1) АÇВ= ВÇА;

2) АÇ( ВÇС)=(АÇВ) ÇС.

По отношению друг к другу операции Ç и È обладают следующими свойствами:

1). (АÈВ) ÇС=(АÇС) È(ВÇС)

(сравните с обычным соотношением из алгебры (a+b)c=ac+bc)

2). (АÇВ)ÈС=(АÈС) Ç(ВÈС)

Для пересечения множеств А₁, А₂,…А_n используют символ .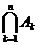

4. Вычитание или разность множеств.

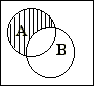Множество С называется разностью множеств А и В (обозначается С=А\В), если оно состоит из элементов, принадлежащих А, но не принадлежащих В. (Это можно записать так: 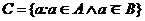). Данный рисунок поясняет эту операцию.

В дальнейшем нам наиболее часто придется иметь дело с двумя множествами.

N={1, 2, 3, 4, ... } – множество всех целых положительных чисел и

Z={0, +1, -1, +2, -2, +3, -3, +4, -4, ... } – множество всех целых чисел.

1.3 Сравнение множеств по числу элементов.

Пусть даны два множества: А={a, b, c} и B={a, b, g}. Спрашивается: в каком множестве больше элементов. Или даны два множества А={a, b, c} и С={1, 2, 3, 4}. Где больше элементов?

Видимо, на этот вопрос ответят все и на дополнительный вопрос: «А как Вы это узнали?» также ответят просто: сосчитали. В множестве А 3 элемента, в множестве В – тоже 3, в множестве С – 4, так что ответ очевиден.

Но вот более сложный вопрос: даны два множества N={1, 2, 3, 4, …} и D={2, 4, 6, 8,…}. В каком множестве больше элементов? И на сам собой напрашивающийся ответ: «конечно, их больше в N. Больше в 2 раза» можно спросить: «А как Вы это узнали? Неужели сосчитали? Но ведь в этих множествах бесконечное число элементов, так что сосчитать Вы никак не могли».

Или: даны 2 отрезка - AB и CD:

На каком отрезке больше точек? И на ответ «Конечно, на CD, ведь он длиннее», так же возразить «Неужели Вы сосчитали точки?»

Поэтому встает проблема сравнения двух множеств по числу элементов, не считая их. И это можно сделать, например, так (см. самый первый пример).

A	a	b	c		A	a	b	c
B	a	b	g		C

В первом случае ясно, что во множествах А и В одинаковое число элементов, а во втором, что в С больше элементов. Заметьте, что в этом случае нет необходимости считать элементы, ответ получается без счета. Оформим этот момент в виде двух точных определений.

Определение 1 Пусть даны два множества А и В. Правило, которое каждому элементу множества А ставит в соответствие элемент множества В, причем так, что каждому элементу множества В оказывается поставленным в соответствие один и только один элемент множества А называется взаимно-однозначным соответствием между множествами А и В.

Теперь ясно, что было сделано. Между множествами А={a, b, c} и B={a, b, g} было установлено взаимно-однозначное соответствие ( 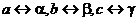), а между множествами А и С этого сделать не удастся.

Определение 2 Если между множествами А и В можно установить взаимно-однозначное соответствие, то говорят, что эти множества эквивалентны по числу элементов (или: «имеют одинаковое число элементов»; или «имеют одинаковую мощность»).

Теперь можно ответить и на вопрос о бесконечных множествах. Рассмотрим множества N и D. Ясно, что между ними можно установить взаимно-однозначное соответствие.

N					…	n	…
D					…	2n	…

И поэтому, в этих множествах одинаковое число элементов. Четных чисел столько же, сколько и всех натуральных!

В отношении двух отрезков вопрос также решается очень просто. Проделав построение, указанное на рисунке, получим, что между точками отрезков АВ и CD установлено взаимно-однозначное соответствие. Таким образом, на этих двух отрезках одинаковое число точек (несмотря на то, что отрезок CD длиннее отрезка АВ).

В чем же была ошибка? Она была в том, что на бесконечные множества были перенесены свойства конечных множеств. Но ведь бесконечность – очень сложная штука, и с ней надо обращаться очень осторожно. Ведь человек – существо конечное (в нем, например, конечное число молекул), как же он может моделировать бесконечные множества?

1.4 Счетные множества.

Определение Множества, эквивалентные по числу элементов множеству N={1, 2, 3, 4, …} называются счетными множествами.

Примеры счетных множеств:

{2, 4, 6, 8, …}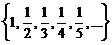

{1, 4, 9, 16, 25, …} {1, 8, 27, 64, 125, …}

Свойства счетных множеств изложим, пользуясь терминологией математики, т.е. громко именуя их теоремами.

Теорема 1. Для того, чтобы множество А было счетным, необходимо и достаточно, чтобы его можно было представить в виде А={a₁, a₂, a₃,…} (то есть в так называемой форме последовательности).

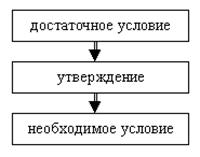
Прежде, чем доказывать эту теорему, напомним, что такое необходимое и что такое достаточное условие. Пусть имеется некоторое утверждение. Любое следствие из него называется необходимым условием этого утверждения.

Любое условие, из которого следует наше утверждение, называется достаточным условием.

Соотношение между этими понятиями может быть пояснено и таким рисунком:

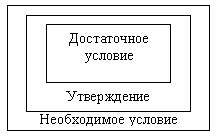
Можно написать и так:

Достаточное условие Ì утверждение Ì необходимое условие.

То, что нам надо доказать, выглядит теперь так:

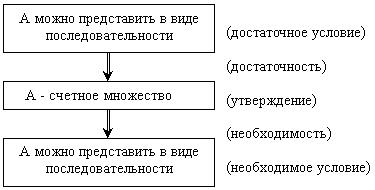
Ну, а теперь

Доказательство

Достаточность Пусть А можно представить в форме последовательности А={a₁, a₂, a₃,…}. тогда следующее правило дает взаимно-однозначное соответствие между А и N.

А	a1	a2	a3	…	an	…
N				…	n	…

Следовательно А – счетно.

Необходимость. Пусть А счетно. Тогда есть правило, устанавливающее взаимно-одно­значное соответствие между А и N. Пусть числу nÎN поставлен в соответствие элемент из А, который мы обозначим через a_n. Тогда А можно представить в виде А={a₁, a₂, a₃,…}, то есть в форме последовательности. < (знак < означает конец доказательства).

Теорема 2. Из всякого бесконечного множества А можно выделить счетное множество.

Доказательство.

Пусть А – бесконечное множество. Возьмем произвольный элемент а₁ÎА. Тогда множество А\{а₁} будет по-прежнему бесконечным.

Из множества А\{а₁} возьмем произвольный элемент а₂ÎА\{а₁}. Множество А\{а₁, a₂} будет по-прежнему бесконечным.

Из множества А\{а₁, a₂} возьмем произвольный элемент а₃Î А\{а₁, a₂}. Множество А\{а₁, a₂, а₃} будет по-прежнему бесконечным.

Продолжая этот процесс до бесконечности, мы получим счетное множество В={a₁, a₂, a₃,…}, для которого очевидно, что ВÌА, то есть В является подмножеством А.<

Доказательство

То, что отрезок [0,1] есть бесконечное множество – очевидно.

1. Предположим противное, то есть то, что отрезок [0,1] есть счетное множество. Тогда все его точки 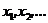можно представить в форме последовательности .

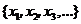( Обратите внимание на слова «все его точки». В последовательности стоят именно точки, а не изображающие их числа! ).

2. Поставим каждой точке в соответствие вещественное число, согласно описанной выше процедуре. Ясно, что все эти числа будут иметь знак + и их цифра перед запятой будет равна 0.

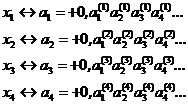
Обратите внимание на то, что вместо точек появились числа, и на индексацию цифр. Чему соответствует верхний индекс и что определяет нижний индекс?

3. Построим особое число .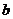

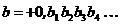
по следующему правилу:

а) его знак +, перед запятой стоит 0

б) первая цифра после запятой – любая, кроме .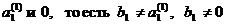

в) вторая цифра после запятой – любая, кроме .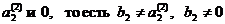

…………………………………

г) вообще, n-я цифра после запятой – любая, кроме .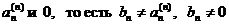

Обратите внимание, что при построении 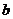снова был использован прием диагонализации. Требование 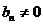связано с запретом на числа вида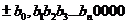

4. Что же хорошего можно сказать о точке 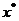, соответствующей числу ?

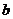а) во-первых ясно, что 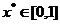: об этом говорит то, что перед запятой стоит комбинация +0.

б) но, с другой стороны, ; ; 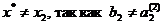… Вообще, для любого n . Поэтому

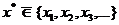
Вот тут и кроется противоречие. Ведь в п.1 предполагалось, что в последовательности 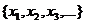перебраны все точки интервала [0,1]. И вдруг оказалась, что есть еще одна точка из этого же интервала, которой нет в этой последовательности. Получившееся противоречие доказывает нашу теорему. <

Определение. Множества, эквивалентные по числу элементов отрезку [0,1] называются множествами мощности континуума.

Терминология. Неравенства.

В заключение этого раздела уточним еще раз некоторые термины.

Множество чисел х, удовлетворяющее свойству a£x£ b, называется замкнутым отрезком и обозначается [a, b].

Множество чисел х, удовлетворяющее свойству a<x<b, называется открытым отрезком и обозначается (a, b).

Множество чисел х, удовлетворяющее свойству a<x£ b (или a£ x<b), называется полуоткрытым отрезком и обозначается (a, b] (соответственно [a, b)).

Модулем |x| числа х называется это же число, взятое со знаком «+». Очевидно, что всегда

-| x | £ x £ | x |

Важнейшее в дальнейшем для нас неравенство выглядит так: | x + y | £ | x | + | y |. Докажем его.

Имеем: -| x | £ x £ | x |; -| y | £ y £ | y |.

Складывая эти неравенства получим:

- (| x | + | y |) £ x + y £ | x | + | y |,

откуда и следует, что | x + y | £ | x | + | y | <

Отметим еще, что | x – y | £ | x | + | y |. Попытка записать это неравенство в виде

| x – y | £ | x | - | y | является грубейшей ошибкой. Никогда не допускайте ее!

Отметим еще, что неравенство 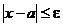эквивалентно такой цепочке:

.

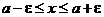Действительно, из 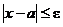следует, что 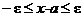, так как 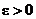и 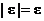. Прибавляя ко всем частям этой цепочки неравенств число а, получим .

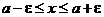Итак, запомните эквивалентную запись:

.

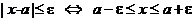Она будет основной в следующем разделе.

Открытый промежуток 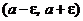называют «e-окрестностью» числа а (или «e-окрест­ностью» точки а).

ГЛАВА 1. Множества. Вещественные числа

Множества

Понятие множества является первоначальным математическим понятием, то есть таким понятием, которое можно только показать на примерах. Можно говорить, например, о множестве людей, находящихся в данной аудитории, о множестве четных чисел, о множестве точек отрезка и т.п. Множества мы будем в дальнейшем обозначать большими латинскими буквами, например, A, B, C и т.д. Иногда множества будут задаваться просто перечислением их элементов и для этого будет использоваться запись вида A={a}, где в {…} будут перечисляться элементы множества A. Например, A={a, b, c} есть множество, состоящее из элементов a, b и c.

Обозначение aÎA означает, что элемент a принадлежит множеству A, а обозначение 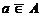или aÏA означает, что элемент a не принадлежит множеству A. Знаком Æ будет обозначаться так называемое пустое множество, то есть такое множество, в котором нет ни одного элемента.

Операции над множествами

1. Вхождение или включение множеств.

Говорят, что множество А входит во множество В (обозначение АÌВ) или множество В включает множество А (обозначение ВÉА) если из того, что некоторый элемент aÎA следует, что aÎВ (запись ).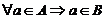

Эту операцию можно пояснить следующим рисунком. Из него видно, что если АÌВ, то множество В шире множества А, то есть содержит бóльшее число элементов.

Если одновременно АÌВ и ВÌА, то означает, что множества А и В совпадают, или равны друг другу (обозначение А=В).

2. Объединение или сумма множеств.

Множество С называют объединением или сумой множеств А и В (обозначение С=АÈВ) если оно состоит из элементов, принадлежащих хотя бы одному из множеств А и В, то есть aÎС означает, что aÎA, или aÎВ или aÎи А и В одновременно. Это можно записать так: 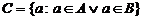, где знак Ú есть символ логического сложения (читается «или»). Эта операция может быть пояснена следующим рисунком.

Операция È обладает обычными свойствами:

1) АÈВ= ВÈА;

2) АÈ( ВÈС)=(АÈВ) ÈС.

Для суммы множеств А₁, А₂,…, А_n используют обозначение .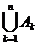

3. Пересечение или произведение множеств.

Множество С называется пересечением или произведением множеств А и В (обозначается С=АÇВ) если оно состоит из элементов, принадлежащих одновременно и множеству А и множеству В. Это можно записать так: 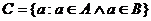где знак Ù есть символ логического умножения (читается «и»). Эта операция может быть пояснена следующим рисунком.

Операция Ç обладает свойствами:

1) АÇВ= ВÇА;

2) АÇ( ВÇС)=(АÇВ) ÇС.

По отношению друг к другу операции Ç и È обладают следующими свойствами:

1). (АÈВ) ÇС=(АÇС) È(ВÇС)

(сравните с обычным соотношением из алгебры (a+b)c=ac+bc)

2). (АÇВ)ÈС=(АÈС) Ç(ВÈС)

Для пересечения множеств А₁, А₂,…А_n используют символ .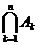

4. Вычитание или разность множеств.

Множество С называется разностью множеств А и В (обозначается С=А\В), если оно состоит из элементов, принадлежащих А, но не принадлежащих В. (Это можно записать так: 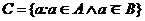). Данный рисунок поясняет эту операцию.

В дальнейшем нам наиболее часто придется иметь дело с двумя множествами.

N={1, 2, 3, 4, ... } – множество всех целых положительных чисел и

Z={0, +1, -1, +2, -2, +3, -3, +4, -4, ... } – множество всех целых чисел.

1.3 Сравнение множеств по числу элементов.

Пусть даны два множества: А={a, b, c} и B={a, b, g}. Спрашивается: в каком множестве больше элементов. Или даны два множества А={a, b, c} и С={1, 2, 3, 4}. Где больше элементов?

Видимо, на этот вопрос ответят все и на дополнительный вопрос: «А как Вы это узнали?» также ответят просто: сосчитали. В множестве А 3 элемента, в множестве В – тоже 3, в множестве С – 4, так что ответ очевиден.

Но вот более сложный вопрос: даны два множества N={1, 2, 3, 4, …} и D={2, 4, 6, 8,…}. В каком множестве больше элементов? И на сам собой напрашивающийся ответ: «конечно, их больше в N. Больше в 2 раза» можно спросить: «А как Вы это узнали? Неужели сосчитали? Но ведь в этих множествах бесконечное число элементов, так что сосчитать Вы никак не могли».

Или: даны 2 отрезка - AB и CD:

На каком отрезке больше точек? И на ответ «Конечно, на CD, ведь он длиннее», так же возразить «Неужели Вы сосчитали точки?»

Поэтому встает проблема сравнения двух множеств по числу элементов, не считая их. И это можно сделать, например, так (см. самый первый пример).

A	a	b	c		A	a	b	c
B	a	b	g		C

В первом случае ясно, что во множествах А и В одинаковое число элементов, а во втором, что в С больше элементов. Заметьте, что в этом случае нет необходимости считать элементы, ответ получается без счета. Оформим этот момент в виде двух точных определений.

Определение 1 Пусть даны два множества А и В. Правило, которое каждому элементу множества А ставит в соответствие элемент множества В, причем так, что каждому элементу множества В оказывается поставленным в соответствие один и только один элемент множества А называется взаимно-однозначным соответствием между множествами А и В.

Теперь ясно, что было сделано. Между множествами А={a, b, c} и B={a, b, g} было установлено взаимно-однозначное соответствие ( 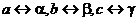), а между множествами А и С этого сделать не удастся.

Определение 2 Если между множествами А и В можно установить взаимно-однозначное соответствие, то говорят, что эти множества эквивалентны по числу элементов (или: «имеют одинаковое число элементов»; или «имеют одинаковую мощность»).

Теперь можно ответить и на вопрос о бесконечных множествах. Рассмотрим множества N и D. Ясно, что между ними можно установить взаимно-однозначное соответствие.

N					…	n	…
D					…	2n	…

И поэтому, в этих множествах одинаковое число элементов. Четных чисел столько же, сколько и всех натуральных!

В отношении двух отрезков вопрос также решается очень просто. Проделав построение, указанное на рисунке, получим, что между точками отрезков АВ и CD установлено взаимно-однозначное соответствие. Таким образом, на этих двух отрезках одинаковое число точек (несмотря на то, что отрезок CD длиннее отрезка АВ).

В чем же была ошибка? Она была в том, что на бесконечные множества были перенесены свойства конечных множеств. Но ведь бесконечность – очень сложная штука, и с ней надо обращаться очень осторожно. Ведь человек – существо конечное (в нем, например, конечное число молекул), как же он может моделировать бесконечные множества?

1.4 Счетные множества.

Определение Множества, эквивалентные по числу элементов множеству N={1, 2, 3, 4, …} называются счетными множествами.

Примеры счетных множеств:

{2, 4, 6, 8, …}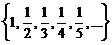

{1, 4, 9, 16, 25, …} {1, 8, 27, 64, 125, …}

Свойства счетных множеств изложим, пользуясь терминологией математики, т.е. громко именуя их теоремами.

Теорема 1. Для того, чтобы множество А было счетным, необходимо и достаточно, чтобы его можно было представить в виде А={a₁, a₂, a₃,…} (то есть в так называемой форме последовательности).

Прежде, чем доказывать эту теорему, напомним, что такое необходимое и что такое достаточное условие. Пусть имеется некоторое утверждение. Любое следствие из него называется необходимым условием этого утверждения.

Любое условие, из которого следует наше утверждение, называется достаточным условием.

Соотношение между этими понятиями может быть пояснено и таким рисунком:

Можно написать и так:

Достаточное условие Ì утверждение Ì необходимое условие.

То, что нам надо доказать, выглядит теперь так:

Ну, а теперь

Доказательство

Достаточность Пусть А можно представить в форме последовательности А={a₁, a₂, a₃,…}. тогда следующее правило дает взаимно-однозначное соответствие между А и N.

А	a1	a2	a3	…	an	…
N				…	n	…

Следовательно А – счетно.

Необходимость. Пусть А счетно. Тогда есть правило, устанавливающее взаимно-одно­значное соответствие между А и N. Пусть числу nÎN поставлен в соответствие элемент из А, который мы обозначим через a_n. Тогда А можно представить в виде А={a₁, a₂, a₃,…}, то есть в форме последовательности. < (знак < означает конец доказательства).

Теорема 2. Из всякого бесконечного множества А можно выделить счетное множество.

Доказательство.

Пусть А – бесконечное множество. Возьмем произвольный элемент а₁ÎА. Тогда множество А\{а₁} будет по-прежнему бесконечным.

Из множества А\{а₁} возьмем произвольный элемент а₂ÎА\{а₁}. Множество А\{а₁, a₂} будет по-прежнему бесконечным.

Из множества А\{а₁, a₂} возьмем произвольный элемент а₃Î А\{а₁, a₂}. Множество А\{а₁, a₂, а₃} будет по-прежнему бесконечным.

Продолжая этот процесс до бесконечности, мы получим счетное множество В={a₁, a₂, a₃,…}, для которого очевидно, что ВÌА, то есть В является подмножеством А.<