Теоремы о функциях, имеющих производную
Теорема Ферма
Теорема. Пусть функция  определена и непрерывна на промежутке
определена и непрерывна на промежутке 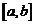 и в некоторой внутренней точке
и в некоторой внутренней точке 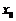 этого промежутка достигает своего наибольшего или наименьшего значения. Если в этой точке существует производная, то она равна нулю:
этого промежутка достигает своего наибольшего или наименьшего значения. Если в этой точке существует производная, то она равна нулю: 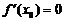 .
.
Доказательство
Пусть, для определенности, в точке 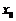 функция
функция  достигает своего наибольшего значения.
достигает своего наибольшего значения.
По условию теоремы эта точка внутренняя, то есть 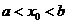 , и поэтому к этой точке можно подойти и слева и справа.
, и поэтому к этой точке можно подойти и слева и справа.
Пусть мы подходим к 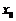 слева. Тогда
слева. Тогда
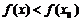 (так как
(так как 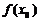 - наибольшее значение);
- наибольшее значение);
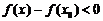 ;
;
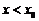 (так как мы подходим слева);
(так как мы подходим слева);
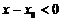 ;
;
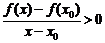 .
.
Делая предельный переход 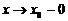 , получим
, получим
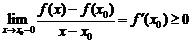 .
.
Пусть мы подходим к точке 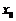 справа. Тогда
справа. Тогда
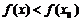 (так как
(так как 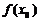 - наибольшее значение);
- наибольшее значение);
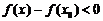 ;
;
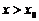 (так как мы подходим слева);
(так как мы подходим слева);
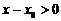 ;
;
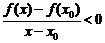 .
.
Делая предельный переход 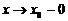 , получим
, получим
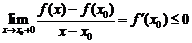 .
.
Совместить два полученных неравенства можно только в одном случае: 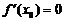 . <
. <
 | Геометрический смысл доказанной теоремы ясен из рисунка: в точке наибольшего или наименьшего значения функции касательная к графику функции параллельна оси OX. |
Существенность ограничений
В теореме Ферма по сути дела два ограничения: а) точка 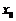 расположена внутри отрезка
расположена внутри отрезка 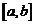 и б)
и б) 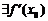 . Покажем, что оба ограничения являются существенными, то есть отказ от любого из них приводит к тому, что утверждение теоремы становится неверным.
. Покажем, что оба ограничения являются существенными, то есть отказ от любого из них приводит к тому, что утверждение теоремы становится неверным.
а) «внутренность» точки 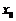 .
.
 | Если максимум или минимум функции  достигается на границе отрезка, то, как видно из рисунка, утверждение теоремы Ферма неверно. При доказательстве это проявляется в том, что мы сможем подойти к точке достигается на границе отрезка, то, как видно из рисунка, утверждение теоремы Ферма неверно. При доказательстве это проявляется в том, что мы сможем подойти к точке 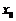 только с одной стороны, и поэтому не получится второго, противоположного неравенства. только с одной стороны, и поэтому не получится второго, противоположного неравенства. |
б) существование производной.
 | Пусть в точке 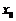 существуют только односторонние производные. Тогда, как это видно из рисунка, теорема Ферма неверна. При доказательстве это проявиться в том, что получаться неравенства существуют только односторонние производные. Тогда, как это видно из рисунка, теорема Ферма неверна. При доказательстве это проявиться в том, что получаться неравенства 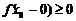 и и 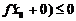 , которые нельзя будет объединить в одно равенство, так как теперь , которые нельзя будет объединить в одно равенство, так как теперь 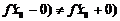 . . |
Теорема Ролля
Пусть функция 
а) определена и непрерывна на 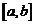 ;
;
б) 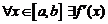 ;
;
в) 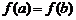
Тогда существует точка 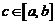 в которой
в которой 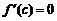 .
.
Доказательство этой теоремы следует из такой логической цепочки рассуждений:
1. Так как  определена и непрерывна на
определена и непрерывна на 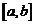 , то, по первой теореме Вейерштрасса, она ограничена на
, то, по первой теореме Вейерштрасса, она ограничена на 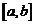 , то есть существуют конечные
, то есть существуют конечные 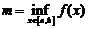 и
и 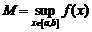 .
.
2. Если 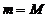 , то
, то  есть константа, то есть
есть константа, то есть 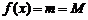 и поэтому
и поэтому 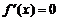
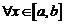 . В качестве точки
. В качестве точки 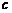 можно взять любую точку из
можно взять любую точку из 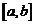 .
.
3. Если 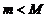 , то, в силу условия
, то, в силу условия 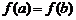 и второй теоремы Вейерштрасса, хотя бы одно из значений
и второй теоремы Вейерштрасса, хотя бы одно из значений 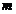 или
или 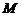 достигается во внутренней точке промежутка
достигается во внутренней точке промежутка 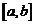 (см. рисунок). По теореме Ферма, в этой точке (их может быть и несколько) производная равна нулю. <
(см. рисунок). По теореме Ферма, в этой точке (их может быть и несколько) производная равна нулю. <
 |  |
| Внутри промежутка достигается sup | Внутри промежутка достигается inf |

Внутри промежутка достигаются и sup и inf.
Формулы Коши и Лагранжа
Теорема. Пусть функции  и
и 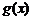
а) определены и непрерывны на 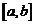 ;
;
б) 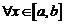
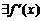 и
и 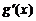 ;
;
в) 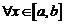
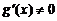 .
.
Тогда существует точка 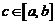 такая, что
такая, что
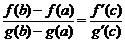 .
.
Эта формула носит название формулы Коши.
Доказательство. Прежде всего отметим, что 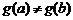 , иначе, по теореме Ролля, существовала бы точка
, иначе, по теореме Ролля, существовала бы точка 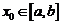 , где
, где 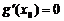 , что противоречит ограничению «в».
, что противоречит ограничению «в».
Рассмотрим функцию
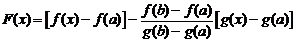 .
.
Она
а) определена и непрерывна на 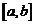 , так как
, так как 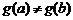 и функции
и функции  и
и 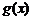 непрерывны на
непрерывны на 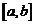 ;
;
б) 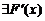
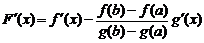 .
.
в) 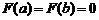 .
.
Таким образом, для 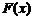 выполнены все условия теоремы Ролля. Поэтому
выполнены все условия теоремы Ролля. Поэтому 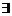
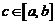 такая, что
такая, что
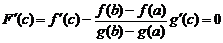 ,
,
но тогда в этой точке 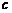
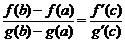 ,
,
что и дает формулу Коши. <
Формула Лагранжа
Рассмотри частный случай, когда 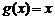 . Тогда формула Коши приобретает вид
. Тогда формула Коши приобретает вид
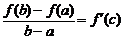 ,
,
или
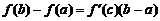 ,
,
где 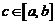 . Эта формула и называется формулой Лагранжа. В дальнейшем мы будем на нее часто ссылаться.
. Эта формула и называется формулой Лагранжа. В дальнейшем мы будем на нее часто ссылаться.
Заметим, что точка 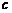 не обязательно единственная: может быть несколько точек
не обязательно единственная: может быть несколько точек 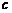 , удовлетворяющих формулам Коши или Лагранжа.
, удовлетворяющих формулам Коши или Лагранжа.
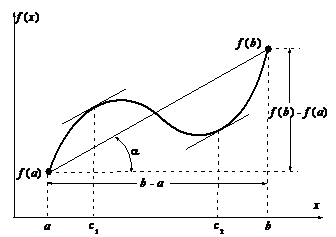 | Рассмотрим еще вопрос о геометрическом смысле формулы Лагранжа. Пусть мы имеем график  . Проведем через точки . Проведем через точки 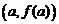 и и 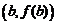 секущую. Она образует с осью OX угол секущую. Она образует с осью OX угол 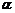 и, как видно из рисунка, и, как видно из рисунка, 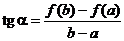 . Но . Но 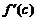 есть тангенс угла, который касательная к кривой в точке есть тангенс угла, который касательная к кривой в точке 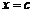 образует с осью OX. Поэтому формулу Лагранжа можно трактовать так: существует точка образует с осью OX. Поэтому формулу Лагранжа можно трактовать так: существует точка 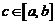 , , |
в которой касательная параллельна секущей, соединяющей точки 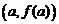 и
и 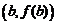 .
.
Дифференциал
Рассмотрим важное для дальнейшего понятие дифференциала.
Напомним, что величина 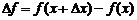 называется приращением функции.
называется приращением функции.
Определение 1. Функция  называется дифференцируемой в точке
называется дифференцируемой в точке 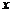 , если ее приращение можно представить в виде
, если ее приращение можно представить в виде
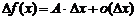 .
.
Определение 2. Линейная часть приращения функции, то есть 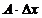 называется дифференциалом функции
называется дифференциалом функции  и обозначается
и обозначается 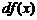
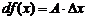 .
.
Чтобы точно уяснить эти определения функции рассмотрим пример. Пусть 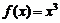 . Тогда
. Тогда
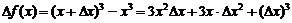
Заметим, что 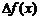 содержит слагаемое, линейное по
содержит слагаемое, линейное по 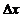 , слагаемые с
, слагаемые с 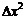 и
и 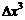 . Так вот, только слагаемое, линейное по
. Так вот, только слагаемое, линейное по 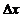 дает дифференциал, то есть
дает дифференциал, то есть
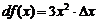 .
.
