Построение стягивающей системы отрезков.

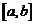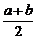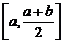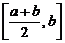Разделим отрезок пополам точкой . Мы получим два отрезка и . Так как на всем отрезке 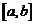имеется бесконечно много членов последовательности, то хотя бы на одной половине также будет бесконечно много членов последовательности. Оставим для дальнейшего рассмотрения эту половину (если на обеих половинах бесконечно много членов последовательности, то оставим любую из них), и назовем ее отрезком .

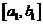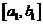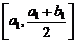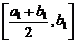Разделим отрезок пополам. Мы получим два отрезка и . Так как на всем отрезке 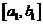находиться бесконечно много членов последовательности, то хотя бы на одной половине также находится бесконечно много членов последовательности. Оставим для дальнейшего рассмотрения эту половину и назовем ее отрезком .

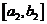Разделим отрезок 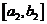пополам. Так как на всем отрезке 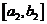находиться бесконечно много членов последовательности, то ....

Продолжим эту процедуру до бесконечности. В результате мы получим систему отрезков 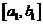, , 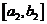, 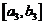…, которые характеризуются тем, что

а) на каждом из них имеется бесконечно много членов последовательности;

б)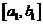

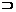
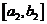
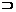
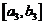
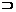
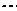
в) .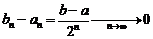

По лемме о вложенных отрезках отсюда следует, что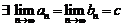

Выделение подпоследовательности

Рассмотрим отрезок 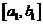и возьмем любой член последовательности .

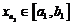Рассмотрим отрезок 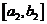и возьмем любой член последовательности 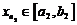. Так как на 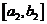бесконечно много членов 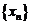, то всегда можно выбрать .

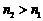Рассмотрим отрезок 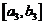и возьмем любой член последовательности 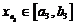. Так как на 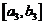бесконечно много членов 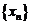, то всегда можно выбрать .

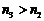Рассмотрим отрезок 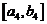и возьмем …

Продолжая эту процедуру до бесконечности, получим подпоследовательность 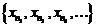такую, что .

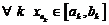Сходимость получившейся подпоследовательности

Так как 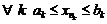и 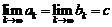то по теореме «о двух милиционерах» .

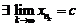Часть 2.Слова «неограниченная последовательность» означают, что .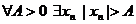

Возьмем последовательность 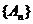такую, что

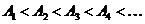и .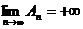

Но тогда для любого A_k существует такое 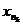, что 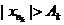. Кроме того, так как в последовательности {x_n} бесконечно много членов, всегда можно добиться того, что будет n_k > n_k-1. В результате получится подпоследовательность 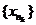, обладающая тем свойством, что "k 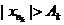. Но тогда

,

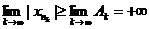откуда и следует, что 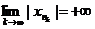, то есть, что 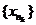- бесконечно большая последовательность.<

Признак Больцано-Коши для последовательности

Признак Больцано-Коши.

Для того, чтобы последовательность 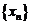сходилась к конечному пределу, необходимо и достаточно, чтобы

.

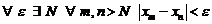Последовательность, удовлетворяющая этому условию называется «фундаментальной последовательностью» или последовательностью, «сходящейся в себе».

Доказательство.

Необходимость. Пусть существует конечный 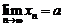. Это значит, что

.

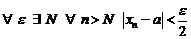Но тогда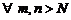

,

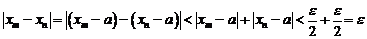что и утверждается в условии теоремы.

Достаточность. Доказательство достаточности гораздо сложнее. Разобьем его на несколько частей.