Существенность ограничений теоремы.
В этой теореме также два ограничения - непрерывность функции 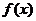 и замкнутость отрезка [a, b]. Покажем на примерах, что отказ от любого из этих ограничений приводит к тому, что теорема становится неверной.
и замкнутость отрезка [a, b]. Покажем на примерах, что отказ от любого из этих ограничений приводит к тому, что теорема становится неверной.
1. Непрерывность функции.
 | Рассмотрим функцию 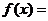 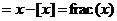 , называемую дробной частью числа х. Ее график приведен на рисунке. Ясно, что супремум этой функции равен 1, но он нигде не достигается. , называемую дробной частью числа х. Ее график приведен на рисунке. Ясно, что супремум этой функции равен 1, но он нигде не достигается. |
2. Замкнутость отрезка.
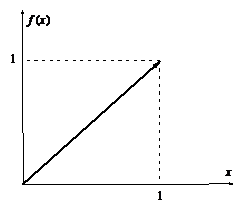 | Рассмотрим функцию 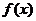 и пусть и пусть 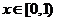 . В этом случае . В этом случае 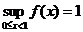 , но этот супремум не достигается, так как точка , но этот супремум не достигается, так как точка 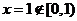 (см. рис.). (см. рис.). |
3.5 Равномерная непрерывность. Теорема Кантора.
Разберем теперь важное и сложное понятие равномерной непрерывности функции.
Пусть имеется функция f(x), которая непрерывна на некотором множестве Х. Вспомним, что это означает: это означает, что f(x) непрерывна в каждой точке этого множества и записывается так:
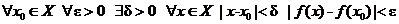 .
.
Обратим внимание на величину d, стоящую после квантора 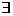 . От чего она зависит?
. От чего она зависит?
Общее правило гласит, что величина, стоящая после квантора 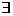 зависит от всех величин, которые стоят после кванторов
зависит от всех величин, которые стоят после кванторов  , которые расположены впереди квантора
, которые расположены впереди квантора 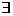 . В данном случае перед
. В данном случае перед 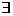 d стоят два квантора
d стоят два квантора 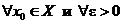 . Поэтому d зависит от e и, и это самое главное, от х0, то есть d=d(e,x0).
. Поэтому d зависит от e и, и это самое главное, от х0, то есть d=d(e,x0).
Так вот, эта зависимость d от х0 очень сильно мешает при доказательстве многих теорем. Хотелось бы, чтобы d зависело только от e и не зависело от х0, то есть d было бы одинаково пригодно для всех х0Î Х. Это желание избавиться от зависимости d от х0 и приводит к понятию равномерной непрерывности.
Определение. Функция f(x) называется равномерно непрерывной на множестве Х, если
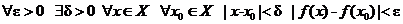 .
.
Обратите внимание на то, куда преместился квантор  . Теперь он стоит после квантора
. Теперь он стоит после квантора 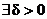 и поэтому d зависит теперь только от e, и не зависит от х0. Это местоположение квантора
и поэтому d зависит теперь только от e, и не зависит от х0. Это местоположение квантора  и есть главное в понятии равномерной непрерывности f(x) на множестве Х.
и есть главное в понятии равномерной непрерывности f(x) на множестве Х.
А теперь докажем достаточно сложную теорему о равномерной непрерывности f(x).
Теорема Кантора. Пусть функция f(x) определена и непрерывна на замкнутом отрезке [a, b]. Тогда она равномерно непрерывна на этом отрезке.
Доказательство.
Доказательство этой теоремы проведем методом от противного.
Надо доказать:
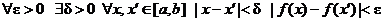 .
.
Противоположное утверждение:
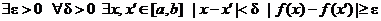 .
.
1. Построение последовательностей.
Возьмем то e>0, которое, согласно противоположному утверждению, «существует».
Возьмем любую последовательность dn, которая монотонно убывает до нуля, то есть
d1>d2>d3>…dn®0, при n ®¥.
Тогда для каждого dn
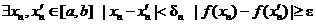 .
.
Перебирая все dn мы получим две последовательности {xn} и 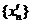 .
.
2. Выделение сходящихся подпоследовательностей. Рассмотрим последовательность {xn}. Она ограничена, так как 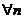 a£xn£b. По лемме Больцано-Вейерштрасса, из нее можно выделить сходящуюся подпоследовательность
a£xn£b. По лемме Больцано-Вейерштрасса, из нее можно выделить сходящуюся подпоследовательность  , то есть для которой
, то есть для которой 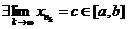 . Заметим, что cÎ[a, b] в силу замкнутости [a, b].
. Заметим, что cÎ[a, b] в силу замкнутости [a, b].
А что можно сказать о подпоследовательности 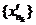 ? Так как
? Так как 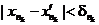 , то
, то
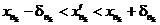 .
.
Но так как 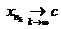 а
а 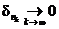 то по теореме «о двух милиционерах» отсюда следует, что также
то по теореме «о двух милиционерах» отсюда следует, что также 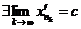 , то есть подпоследовательность
, то есть подпоследовательность 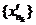 сходится к тому же пределу c, что и
сходится к тому же пределу c, что и  .
.
3. Сведение к противоречию.
Рассмотрим теперь последний квантор
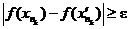 .
.
Переходя к пределу k®¥ и учитывая непрерывность функции y=|x|, получим:
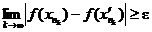 ,
,
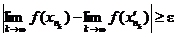 .
.
В силу непрерывности f(x) 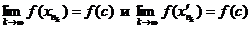 , так что получаем, что
, так что получаем, что
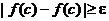 ,
,
то есть получаем, что e£0. Это противоречит квантору 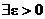 , где e строго больше 0. <
, где e строго больше 0. <
Монотонные функции.
Докажем теперь две теоремы, касающиеся непрерывности монотонных функций.
Теорема 1. Пусть f(x) определена и монотонна на замкнутом отрезке [a, b]. Тогда она может иметь на этом отрезке только разрывы I рода (скачки).
Доказательство.
Пусть, для определенности, f(x) монотонно возрастает.
 | Возьмем какую-то точку x0 Î[a, b]. Пусть мы приближаемся к точке х0 слева (см. рис.). Тогда при этом значения функции f(x) будут монотонно возрастать. Но они будут ограничены сверху, например, величиной f(x0). Поэтому, по теореме о пределе монотонно возрастающей функции будет существовать конечный  . При движении к х0 справа значения f(x) будут монотонно убывать, но будут ограничены снизу величиной f(x0). Поэтому снова существует конечный . При движении к х0 справа значения f(x) будут монотонно убывать, но будут ограничены снизу величиной f(x0). Поэтому снова существует конечный  . . |
Если f(x0+0) = f(x0-0), то f(x) будет непрерывна в точке х0, если же f(x0+0)>f(x0-0), то у f(x) в точке х0 будет разрыв I рода. <
Определение. Говорят, что значения функции f(x), определенной на <a, b>, заполняют некоторый отрезок <c, d> сплошь, если
 .
.
Теорема 2. Для того, чтобы монотонная функция f(x) была непрерывной на [a, b], необходимо и достаточно, чтобы ее значения заполняли отрезок [f(a), f(b)] сплошь.
Доказательство.
Пусть, для определенности, f(x) монотонно возрастает.
1. Достаточность. Пусть f(x) непрерывна на [a, b]. Тогда  ,
,  . Согласно второй теореме Больцано-Коши,
. Согласно второй теореме Больцано-Коши,
 .
.
Поэтому отрезок [f(a), f(b)] заполнен сплошь.
2. Необходимость. При доказательстве необходимости в этой теореме используется достаточно редко применяемый прием. Он основан на следующем соотношении из алгебры логики
 .
.
Вместо того, чтобы доказывать, что  доказывают, что
доказывают, что  .
.
В нашем случае это выглядит так: вместо того, чтобы доказывать следование «функция заполняет некоторый отрезок сплошь Þ она непрерывна», доказывают следование «функция не непрерывна Þ ее значения не заполняют отрезок сплошь».
Итак: пусть f(x) не является непрерывной на [a, b]. Тогда она на [a, b] может иметь только разрывы I рода. Пусть х0 – координата такого разрыва. Возможные варианты поведения графика f(x) изображены на рисунках.
  |   |


Из них видно, что в этом случае отрезок [f(a), f(b)] заполнен не сплошь. <
