Расчет параметров ПИ-регулятора по параметрам объекта по регулирующему каналу графоаналитическим методом

Рассчитаем ПИ-алгоритм управления, передаточная функция которого имеет вид:

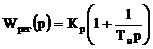, (3.1)

а параметрами, подлежащими определению, являются коэффициент усиления К_р и постоянная интегрирования Т_и, для этого используем графоаналитический метод.[3]

С помощью программы «СС» строим АФХ объекта по передаточной функции (1.5) (приложение 1)

1. По АФХ объекта W_об^u-y (jω) строим семейство характеристик разомкнутой системы W_раз(jω) для К_р = 1 и нескольких фиксированных значений постоянной интегрирования Т_и.

Для этого сначала строим несколько векторов характеристики объекта W_об^u-y (jω), например, векторы 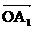для частоты ω₁, 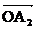для ω₂ и т.д. (приложение 1).

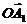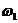· для = 0,183р/c, 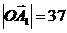мм

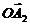· для 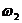=0,237р/c, 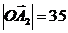мм

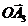· для 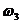=0,336р/с, 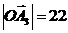мм

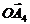· для 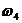=0,461р/с, 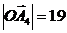мм

К их концам надо пристроить векторы 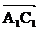, ,…, , 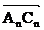повернутые по отношению к векторам 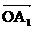, ,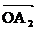…, 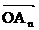на угол 90°. Длина векторов 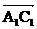, ,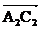…, 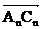выбирается из соотношения 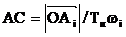(где в числителе - длина вектора АФХ объекта для определённого значения частоты w_i, которую можно измерить непосредственно в миллиметрах; в знаменателе – произведение указанной частоты на фиксированное значение Т_и). Результаты расчёта представлены в таблице 2.

Таблица 2

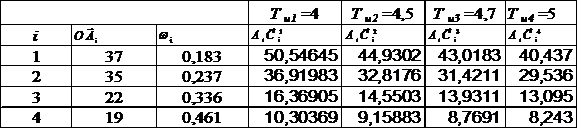
Через полученные точки С₁, С₂,…, С_n проводим плавную кривую, которая является характеристикой W_раз1(jω) для выбранного значения Т_и. Аналогичные построения проводим для других значений Т_и. В итоге получаем семейство характеристик W_раз (jω) для различных значений Т_и.

2. Из начала координат проводим прямую ОЕ под углом b, характеризующим запас устойчивости по фазе и определяемым как:

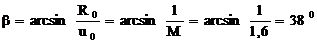. (3.2)

3. С помощью циркуля вычерчиваем окружности с центром на отрицательной вещественной полуоси, каждая из которых касается одновременно как прямой ОЕ, так и одной из характеристик W_раз1(jω) (центр каждой окружности и ее радиус находим подбором).

4. Отношение требуемого радиуса R₀, определяемого по формуле (2.3), к полученному в каждом отдельном случае значению r_i показывает, во сколько раз нужно изменить единичный коэффициент передачи регулятора (К_р=1), чтобы каждая характеристика W_раз1(jω) касалась окружности с заданным М, т.е.

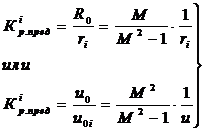. (3.3)

Для вычисления К_{р. пред} использована формула:

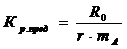, (3.4)

где:

R_о – радиус, определяемый по формуле (2.3);

r – радиус окружности, находящийся методом подбора;

m_A – масштабный коэффициент, из приложения 1, равный m_A = 0,01;

Все результаты вычислений представлены в таблице 3:

Таблица 3

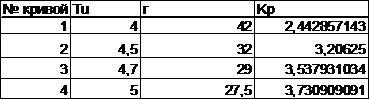
5 В результате в плоскости варьируемых параметров алгоритма К_р и Т_и строится граница области заданного запаса устойчивости (приложение 1).

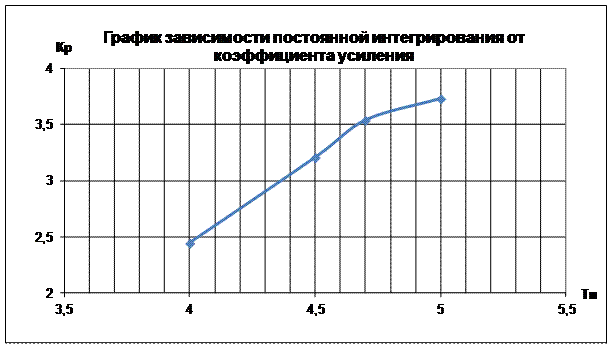Рис.8 График зависимости постоянной интегрирования 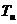от коэффициента усиления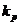

Максимум отношения К_р/Т_и, определяющего оптимальную настройку регулятора при низкочастотных возмущениях, соответствует точке пересечения касательной с границей заданного запаса устойчивости, проведённой через начало координат.

Передаточная функция регулятора, после определения координат точки А (К_р.опт = 3,537 и Т_{и опт} = 4,7)(приложение 1), имеет вид:

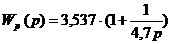
Следует отметить, что найденные таким образом параметры являются оптимальными только при низкочастотном характере возмущений. По мере расширения полосы частот возмущений точка оптимума в плоскости параметров (приложение 1) смещается вправо от точки А, причём сначала это смещение идёт вдоль границы заданного запаса устойчивости, а затем, при достаточно высокочастотных воздействиях, она уходит вглубь области. Это означает, что с ростом частоты воздействий ПИ-алгоритм должен всё более приближаться к П-алгоритму, К_р которого также снижается. Это сопровождается ухудшением эффективности управления.