Методы оценивания моделей бинарного выбора

3.2.1. Метод максимального правдоподобия.Построение регрессионных моделей с использованием нелинейных зависимостей подобного типа практически исключает применение метода наименьших квадратов. Для оценивания моделей бинарного выбора обычно используется метод максимального правдоподобия [2]. Применение этого метода осуществляется в предположении, что каждое наблюдение может трактоваться как однократный выбор из распределения Бернулли. Таким образом, модель с вероятностью успеха и независимыми наблюдениями (эксперты опрашиваются независимо друг от друга) представляет собой вероятность совместного появления всей совокупности ожидаемых событий

. (3.17)

Для каждого вектора , представляющего собой результаты конкретного экспертного опроса, величина вероятности зависит от вектора оцениваемых параметров 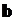и может быть записана как функция правдоподобия

. (3.18)

В данной форме записи множители произведения селектируются с помощью компонент вектора , принимающих всего два значения: 0 или 1.

Удобнее и математически проще максимизировать логарифмическую функцию правдоподобия

. (3.19)

Используя сокращенные записи и , выпишем для логарифмической функции правдоподобия условия максимизации первого порядка

. (3.20)

Подставляя в полученное выражение логистическое распределение, получаем после очевидных преобразований следующую систему уравнений:

. (3.21)

В случае нормального распределения система уравнений имеет вид

. (3.22)

Введение в рассмотрение переменной , позволяет переписать эту систему следующим образом:

. (3.23)

Полученные системы уравнений нелинейны, и для их решения необходимо применять численные методы. Прежде чем приступить к численному решению следует убедиться в том, что итерационная процедура обеспечивает получение глобального максимума логарифмической функции правдоподобия. Для этого покажем, что эта функция является строго вогнутой, т.е. имеет единственный максимум.

Чтобы убедиться в этом, достаточно показать, что и являются строго вогнутыми. Из этого, в силу того, что сумма строго вогнутых функций есть строго вогнутая функция, будет следовать, что, и логарифмическая функция правдоподобия строго вогнута.

Основным признаком строгой вогнутости является отрицательность второй производной. Сначала покажем, что этим свойством обладает . Последовательно дифференцируя, получаем

; (3.24)

. (3.25)

В соответствии с полученными выражениями для логистической функции имеем

; (3.26)

; (3.27)

. (3.28)

Строгая вогнутость доказана. Так как в случае логистической функции симметрична , то она тоже строго вогнута. Следовательно, логарифмическая функция правдоподобия, представляющая собой сумму строго вогнутых функций, сама является строго вогнутой, и применение градиентной процедуры приводит к получению единственного решения.

В случае, когда является функцией нормального распределения, результат тот же самый – логарифмическая функция правдоподобия строго вогнута. Таким образом, численное решение системы (3.21) или (3.23) приводит к получению оценок, максимизирующих соответствующие функции правдоподобия.

3.2.2. Численное решение с помощью метода Ньютона – Рафсона.Рассмотрим построенную на основе метода Ньютона – Рафсона вычислительную схему решения нелинейной системы уравнений

. (3.29)

Все детали этой схемы будут изложены без уточнения, на основе какого распределения была построена функция правдоподобия.

Считая левую часть системы (3.29) дифференцируемой вектор-функцией (для исследуемых здесь распределений это действительно так), запишем отрезок ряда Тейлора, являющегося линейной аппроксимацией этой функции в окрестности некоторой точки

. (3.30)

Производная по обозначает производную по 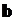, вычисленную в точке . Саму точку будем считать начальным приближением искомой оценки. Ее значение можно определить как вектор параметров линейной регрессии

, (3.31)

оцененных с помощью метода наименьших квадратов, т.е.

. (3.32)

Обозначив произвольную точку окрестности через и помня, что нашей целью является нахождение такого вектора параметров, который обращает первую производную в ноль, целесообразно записать

. (3.33)

Раскрывая круглые скобки и перенося влево член, содержащий , а затем, умножая обе части уравнения на обратную матрицу, получаем выражение, задающее итерационный процесс нахождения искомого решения

. (3.34)

Вектор является первой оценкой искомых параметров. Вычисляя значения производных во вновь получаемых точках, и продолжая итерационный процесс по рекуррентной формуле

, (3.35)

получаем последовательность . Если предел этой последовательности равен 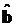, то этот предел есть искомое решение системы, так как соотношение

(3.36)

имеет смысл при

. (3.37)

Следовательно, полученное решение является также и оценкой максимального правдоподобия.

3.2.3. Итерационная схема обобщенного МНК (метод Берксона).В некоторых ситуациях появляется возможность для оценки параметров логит- и пробит-моделей применять метод наименьших квадратов [16]. Подобная ситуация возникает в случае «повторяющихся» (или группированных) статистических наблюдений, имеющих структуру вида

(3.38)

. . . . . . . . . . .

В каждой k-ойгруппе наборы независимых переменных равны между собой, т.е. , где . Фактически имеет место ситуация, когда в выборке имеется по несколько наблюдений зависимой переменной y соответствующих одним и тем же значениям объясняющих переменных (либо в группе все наборы объясняющих переменных, в силу того, что мало отличаются друг от друга, заменены одним и тем же набором с усредненными значениями ).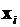

В этом случае функция правдоподобия приобретает следующий вид:

. (3.39)

Если все достаточно велики, то можно вместо максимизации логарифмической функции правдоподобия для получения оценок параметров модели применить схему метода взвешенных наименьших квадратов. С этой целью перейдем от исходного набора наблюдений можно к наблюдениям вида

, (3.40)

где – относительная частота события, состоящего в том, что зависимая переменная примет значение равное единице при значениях объясняющих переменных, равных .

В соответствии с теоремой Бернулли относительная частота связана с истинным значением вероятности неравенством

, (3.41)

которое позволяет записать соотношение

. (3.42)

Случайная составляющая имеет нулевое математическое ожидание и дисперсию равную .

Таким образом, соотношение для относительной частоты можно рассматривать как нелинейную регрессию с гетероскедастичными (т.е. имеющими не равные дисперсии) остатками. Параметры такой регрессии оцениваются с помощью итерационной вычислительной процедуры минимизирующей взвешенную сумму квадратов

. (3.43)

Упростить построение нелинейной регрессии можно в том случае, если удается подобрать такое преобразование, которое позволяет заменить нелинейную модель линейной, которая эквивалентна исходной в смысле совпадения оцениваемых параметров. Таким преобразованием является функция обратная функции распределения вероятности соответствующего закона. Если операцию обращения применить к (3.42), то получается соотношение

, (3.44)

представляющее собой линейную регрессию, обоснованность которой приводится ниже.

Промежуточное представление при переходе от (3.42) к (3.44)

(3.45)

можно в окрестности точки разложить в ряд Тейлора, и ограничившись точностью первого порядка, записать следующим образом:

, (3.46)

где

,

а остаточный член легко преобразуется к виду

. (3.47)

В преобразованном остаточном члене величина равна значению функции плотности закона распределения вероятности в точке .

Введение обозначений и позволяет записать уравнение регрессии (3.44). Зависимая переменная в этом уравнение представляет собой квантиль уровня функции распределения . Случайные составляющие имеют нулевые математические ожидания и неравные дисперсии .

В результате проведенных преобразований задача построения нелинейных логит- и пробит-моделей свелась к оценке параметров линейной функции регрессии с гетероскедастичными остатками. В качестве зависимых переменных в этих функциях регрессии используются квантили соответствующих распределений. В логит-моделях для расчета квантиля используется функция

, (3.48)

которая является решением уравнения

(3.49)

относительно , т.е. действительно определяет квантиль уровня .

В пробит-моделях значения зависимой переменной определяются в виде табличных квантилей уровня стандартного нормального распределения.

После преобразования моделей к линейному виду их построение осложняется только гетероскедастичностью остатков . Как известно, избежать возможного искажения коэффициентов удается путем применения взвешенного метода наименьших квадратов. В качестве весовых коэффициентов в этом методе используются величины, обратные дисперсии соответствующих остатков . Для логит-модели весовые коэффициенты определяются из соотношения

. (3.50)

Таким образом, оценка параметров логит-модели сводится к решению оптимизационной задачи вида

, (3.51)

где рассчитано по формуле (5.3.10), определяется в соответствии с (3.50).

Оценка параметров пробит-модели сводится к решению этой же оптимизационной задачи, но с другими значениями зависимой переменной и другими весовыми коэффициентами. Для пробит-модели значения зависимой переменной определяются в виде табличных квантилей уровня стандартного нормального распределения, а весовые коэффициенты определяются по формуле

, (3.52)

в которой – функция плотности, а – функция распределения стандартного нормального закона вероятности.

При фиксированных значениях весовых коэффициентов решение оптимизационной задачи (3.51) легко получается с помощью обобщенной процедуры метода наименьших квадратов. Однако в рассматриваемом здесь случае веса зависят от оцениваемых параметров и решение оптимизационной задачи можно получить, применив итерационную процедуру. На первом шаге этой процедуры оптимизация (3.51) проводится с помощью обобщенного метода наименьших квадратов при . Полученные оценки используются для подсчета по соответствующим формулам весовых коэффициентов или в зависимости от модели (логит-модель или пробит-модель). Эти новые коэффициенты используются в обобщенном методе наименьших квадратов на следующем шаге итерационной процедуры для получения оценок . Итерационная процедура продолжается до тех пор, пока пересчитанные весовые коэффициенты очередного шага не совпадут до определенного знака после запятой с весовыми коэффициентами предыдущего шага.

Подобного рода итерационные процедуры используются во многих статистических пакетах. В частности, возможность построения моделей бинарного выбора с использованием итерационной процедуры реализована, например, в пакетах Eviews и Statistica.