Условие монотонности функции

Теорема 1.Для того чтобы дифференцированная на интервале(a,b) функция f(x) не убывала (не возрастала) на этом интервале, необходимо и достаточно, чтобы производная этой функции была неотрицательной (неположительной) всюду на этом интервале.

Доказательство. Достаточность. Пусть 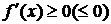всюду на интервале (a,b). Требуется доказать, что f(x) не убывает (не возрастает) на интервале (a,b). Пусть х₁ и х₂ – любые две точки интервала (a,b), удовлетворяющие условию х₁< х₂. Функция f(x) дифференцируема (а стало быть и непрерывна) всюду на сегменте [х₁,х₂]. Поэтому к f(x) можно применить на сегменте [х₁,х₂] теорему Лагранжа, в результате чего получим

f(x₂) – f (x₁) = (х₂ – х₁) f'(ξ), где х₁ < ξ < х₂.

Отсюда (так как по условию f '(ξ) ≥ 0 (≤ 0), (х₂ – х₁) > 0) получаем

f(x₂) ³ f(x₁) (f(x₂) ≤ f(x₁)), что и доказывает неубывание (невозрастание) f(x) на интервале (a,b).

Необходимость. Пусть функция f(x) дифференцируема на интервале (a,b) и не убывает (не возрастает) на этом интервале. Требуется доказать, что 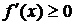(≤ 0) всюду на этом интервале. Придадим аргументу х приращение Δх и рассмотрим отношение .

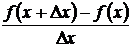Так как f(x) функция неубывающая, то

f(x + Δх) ³ f(x) при Δх > 0 и f(x + Δх) ≤ f(x) при Δх < 0.

В обоих случаях

,

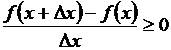а, следовательно,

,

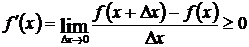что и требовалось доказать.

В рассмотренном случае для монотонной функции f(x) не была исключена возможность сохранять в некоторых промежутках и постоянные значения, а для ее производной – обращаться в этих промежутках тождественно в нуль. Если мы эту возможность исключим, то придем к случаю монотонного возрастания (или убывания) в строгом смысле.

Теорема 2.Для того, чтобы функция f(x) возрастала (убывала) на интервале (а,b), достаточно, чтобы производная 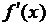была положительной (отрицательной) всюду на этом интервале.

Доказательство проводится по той же схеме, что и доказательство достаточности в предыдущей теореме 1. Пусть х₁ и х₂ – любые две точки интервала (а,b), удовлетворяющие условию х₁ < х₂. Записывая для сегмента [х₁,х₂] формулу Лагранжа, получим f(х₂) > f(х₁), так как на этот раз .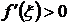

Замечание. Подчеркнем, что положительность (отрицательность) производной 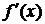на интервале (а,b) не является необходимым условием возрастания (убывания) функции f(x) на интервале (а,b). Так, функция 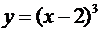возрастает на интервале (0,4), но производная этой функции 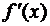= 3(х – 2)² не является всюду положительной на этом интервале (она обращается в нуль в точке х = 2). Вообще, легко доказать, что функция f(x) возрастает (убывает) на интервале (а,b), если производная этой функции 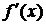положительна (отрицательна) всюду на этом интервале, за исключением конечного числа точек, в которых эта производная равна нулю.

Установленную теоремой 2 связь между знаком производной и направлением изменения функции легко понять из геометрических соображений. Поскольку производная равна угловому коэффициенту касательной к графику функции y = f(x), знак производной указывает, острый или тупой угол с положительным направлением оси Oх составляет луч касательной, лежащий в верхней полуплоскости, т.е. наклонена ли касательная вверх или вниз, а с нею – идет ли вверх или вниз и сама кривая (рис.20).

Однако в отдельных точках x = x₀ касательная при этом может оказаться и горизонтальной (рис.20), т.е. производная – даже в строгом смысле – монотонно возрастающей (убывающей) функции может для отдельных значений x = x₀ обращаться в нуль.

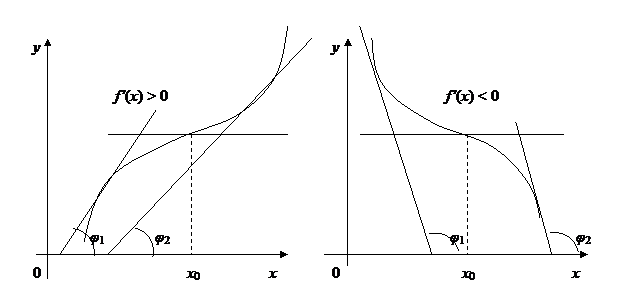
Рис. 20

4.3. Формула Коши (обобщенная формула конечных приращений)

В этом пункте мы докажем теорему, принадлежащую Коши и обобщающую установленную выше теорему Лагранжа.

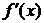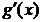Теорема Коши. Пусть функции f(x) и g(x): 1) непрерывны на сегменте [a,b], 2) существуют конечные производные и в каждой точке интервала (а,b), 3) производная функции g(x) на интервале (а,b) не обращается в нуль, тогда в интервале (а,b) найдется такая точка 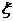, что справедлива формула

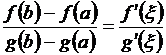, (3.36)

т.е. отношение приращений функций на данном отрезке равно отношению их производных в точке 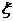. Формулу (3.36) называют обобщенной формулой конечных приращений или формулой Коши.

Доказательство. Установим вначале, что знаменатель левой части равенства (3.36) не равен нулю, так как в противном случае это выражение не имело бы смысла. Если бы было g(b) = g(a), то для функции g(x) были бы выполнены на сегменте [a,b] все условия теоремы Ролля и по этой теореме внутри сегмента [a,b] нашлась бы такая точка 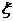, что 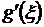= 0. Последнее противоречит условию 3) теоремы; значит, g(b) ¹ g(a).