Раздел II. Введение в анализ
Раздел II. Введение в анализ
Глава 5. Функция
Краткая теория
1. Если каждому элементу (значению)  множества
множества 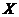 поставить в соответствие определенный элемент (значение)
поставить в соответствие определенный элемент (значение) 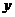 множества
множества 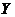 , то говорят, что на множестве
, то говорят, что на множестве 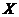 задана функция
задана функция 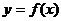 ; при этом множество
; при этом множество 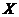 называется областью определения функции
называется областью определения функции 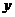 , а множество
, а множество 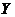 - областью значений функции
- областью значений функции 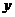 .
.
2. Функция 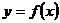 называется четной, если для любых значений
называется четной, если для любых значений  из области определения функции
из области определения функции 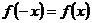 , и нечетной, если
, и нечетной, если 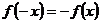 . В противном случае
. В противном случае 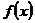 - функция общего вида.
- функция общего вида.
3.Функция 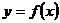 называется возрастающей (убывающей) на некотором промежутке
называется возрастающей (убывающей) на некотором промежутке 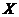 , если большему значению аргумента соответствует большее (меньшее) значение функции
, если большему значению аргумента соответствует большее (меньшее) значение функции 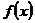 . Возрастающие или убывающие функции называются монотонными.
. Возрастающие или убывающие функции называются монотонными.
4. Функция 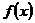 называется ограниченной на промежутке
называется ограниченной на промежутке 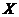 , если существует такое число
, если существует такое число 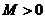 , что
, что 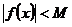 , для всех
, для всех 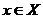 . В противном случае функция называется неограниченной.
. В противном случае функция называется неограниченной.
5. Если функция 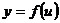 есть функция переменной
есть функция переменной 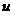 (определенной на множестве
(определенной на множестве 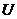 с областью значений
с областью значений 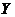 ), а переменная
), а переменная 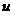 , в свою очередь, также является функцией
, в свою очередь, также является функцией 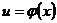 (определенной на множестве
(определенной на множестве 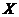 с областью значений
с областью значений 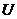 ), то заданная на множестве
), то заданная на множестве 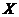 функция
функция 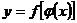 называется сложной функцией.
называется сложной функцией.
6. Основные элементарные функции:
а) степенная функция 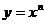 ;
;
б) показательная функция 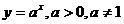
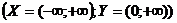 ;
;
в) логарифмическая функция 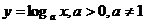
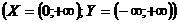 ;
;
г) тригонометрические функции 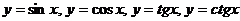 ;
;
д) обратные тригонометрические функции 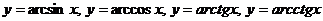 .
.
7. Функции, построенные из основных элементарных функций при помощи конечного числа алгебраических действий и конечного числа операций образования сложной функции, называются элементарными.
8. Функция 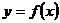 называется периодической с периодом
называется периодической с периодом 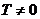 , если
, если 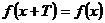 для любых
для любых 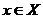 .
.
9.Преобразование графиков:
а) 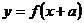 - сдвигает график
- сдвигает график 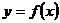 параллельно оси
параллельно оси 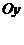 на
на 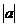 единиц, (
единиц, ( 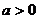 - влево,
- влево, 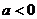 - вправо);
- вправо);
б) 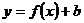 - сдвигает график
- сдвигает график 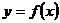 параллельно оси
параллельно оси 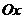 на
на 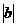 единиц (
единиц ( 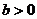 - вверх,
- вверх, 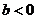 - вниз);
- вниз);
в) 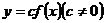 - растягивает в
- растягивает в 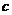 раз
раз 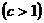 или сжимает
или сжимает 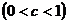 график
график 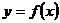 относительно оси
относительно оси 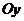 ; при
; при 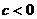 симметрично отображает график относительно оси
симметрично отображает график относительно оси 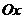 ;
;
г) 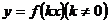 - растягивает в
- растягивает в 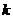 раз
раз 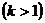 или сжимает
или сжимает 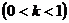 график
график 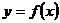 относительно оси
относительно оси 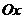 , при
, при 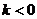 симметрично отображает график относительно оси
симметрично отображает график относительно оси 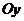 .
.
10.Абсолютная величина (модуль) действительного числа  :
:
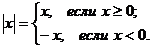
5.1.Найти область определения функции
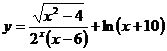 .
.
Решение. Так как выражение под корнем четной степени должно быть неотрицательно, знаменатель дроби отличен от нуля, а выражение, стоящее под знаком логарифма, должно быть положительно, то область определения функции найдем из системы неравенств:
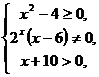 или
или 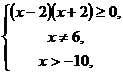 откуда
откуда 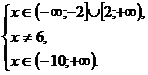
Значения переменной  , которые удовлетворяют всем неравенствам системы одновременно, есть
, которые удовлетворяют всем неравенствам системы одновременно, есть 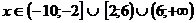 .
.
5.2. Найти область значений функции 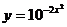 .
.
Решение. Воспользуемся определением обратной функции, в соответствии с которым область ее определения будет являться областью значений исходной функции. Найдем функцию, обратную к функции 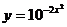 , выражая
, выражая  через
через 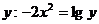 или
или 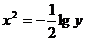 .
.
Так как 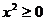 , то
, то 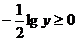 , откуда
, откуда 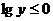 и
и 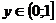 , т.е. найденный полуинтервал и является областью значения искомой функции.
, т.е. найденный полуинтервал и является областью значения искомой функции.
5.3. Выяснить четность (нечетность) функции:
а) 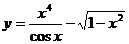 ; б)
; б) 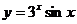 .
.
Решение:
а) Найдем 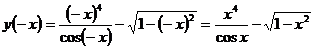
Так как 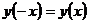 , то по определению (п.2) искомая функция является четной;
, то по определению (п.2) искомая функция является четной;
б) 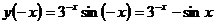 так как
так как 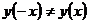 и
и 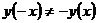 , то по определению (п. 2) искомая функция является функцией общего вида.
, то по определению (п. 2) искомая функция является функцией общего вида.
5.4. Найти основной (наименьший) период функции 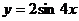 .
.
Решение: По определению периодической функции (п. 8) 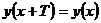 для любых
для любых  и
и 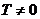 . Для
. Для 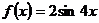 имеем:
имеем:
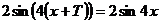 , или
, или 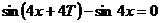 , откуда
, откуда 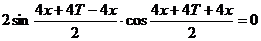 . т.е.
. т.е. 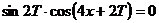 . Полученное равенство будет выполняться при любых
. Полученное равенство будет выполняться при любых  , т.е. тождественно, если сомножитель, не содержащий
, т.е. тождественно, если сомножитель, не содержащий  , будет равен нулю, т.е.
, будет равен нулю, т.е. 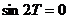 и наименьшее (не равное нулю)
и наименьшее (не равное нулю) 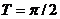 .
.
5.5. Постоянные издержки 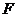 (не зависящие от числа х произведенной продукции) составляют 125 тыс. руб. в месяц, а переменные издержки
(не зависящие от числа х произведенной продукции) составляют 125 тыс. руб. в месяц, а переменные издержки 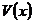 (пропорциональные
(пропорциональные  ) – 700 руб. за каждую единицу продукции. Цена единицы продукции 1200 руб. Найти объем продукции
) – 700 руб. за каждую единицу продукции. Цена единицы продукции 1200 руб. Найти объем продукции  , при котором прибыль равна: а) нулю (точка безубыточности); б) 105 тыс. руб. в месяц.
, при котором прибыль равна: а) нулю (точка безубыточности); б) 105 тыс. руб. в месяц.
Решение:
а) Издержки производства  единиц продукции составят:
единиц продукции составят: 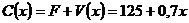 (тыс. руб.). Совокупный доход (выручка) от реализации этой продукции
(тыс. руб.). Совокупный доход (выручка) от реализации этой продукции 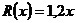 , а прибыль
, а прибыль 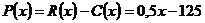 (тыс. руб.). Точка безубыточности, в которой
(тыс. руб.). Точка безубыточности, в которой 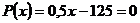 , равна
, равна 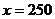 (ед.).
(ед.).
б) прибыль 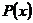 равна 105 (тыс. руб.), т.е.
равна 105 (тыс. руб.), т.е. 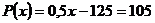 при
при 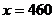 (ед.).
(ед.).
5.6. Продолжительность выполнения 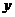 (мин.) при повторных операциях связана с числом
(мин.) при повторных операциях связана с числом  этих операций зависимостью
этих операций зависимостью 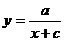 . Вычислить, сколько минут выполняется работа при 50 операциях, если известно, что при
. Вычислить, сколько минут выполняется работа при 50 операциях, если известно, что при 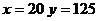 , а при
, а при 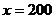
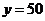 .
.
Решение. Найдем параметры 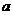 и
и 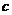 , учитывая, что
, учитывая, что 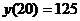 ,
, 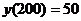 . Имеем систему:
. Имеем систему:
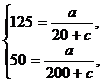
решая которую найдем 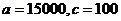 .
.
Итак, 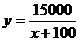 и при
и при 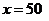
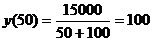 (мин.).
(мин.).
Найти области определения функций:
5.12. 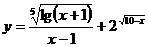 .
.
5.13. 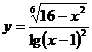 .
.
5.14. 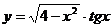 .
.
5.15. 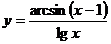 .
.
5.16. 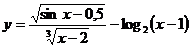 .
.
Найти области значений функций:
5.17. 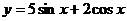 .
.
5.18. 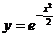 .
.
5.19. 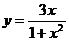 .
.
5.20. 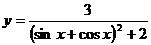 .
.
5.21. 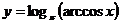 .
.
Выяснить четность (нечетность) функций:
5.22. 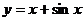 .
.
5.23. 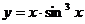 .
.
5.24. 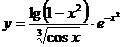 .
.
5.25. 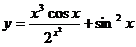 .
.
5.26. 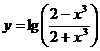 .
.
Найти наименьший период функций или доказать их непериодичность:
5.27. 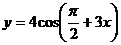 .
.
5.28. 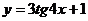 .
.
5.29. 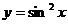 .
.
5.30. 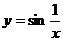 .
.
5.31. 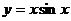 .
.
5.32. Дана функция 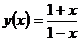 , найти
, найти 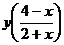 .
.
5.33. Дана функция 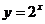 ,найти
,найти 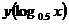 .
.
5.34. Известно, что 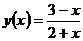 , а
, а 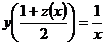 . Найти
. Найти 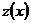 .
.
5.35. Известно, что 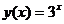 , а
, а 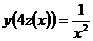 . Найти
. Найти 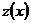 .
.
5.38. Предприятие купило автомобиль стоимостью 150 тыс. руб. Ежегодная норма амортизации составляет 9 %. Полагая зависимость стоимости автомобиля от времени линейной, найти стоимость автомобиля через 4,5 года.
5.39. Зависимость уровня потребления 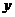 некоторого вида товаров от уровня дохода семьи
некоторого вида товаров от уровня дохода семьи  выражается формулой:
выражается формулой: 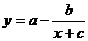 . Найти уровень потребления товаров при уровне дохода семьи 158 ден. ед. Известно, что при
. Найти уровень потребления товаров при уровне дохода семьи 158 ден. ед. Известно, что при 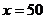
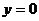 ; при
; при 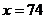
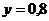 ; при
; при 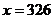
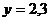 .
.
5.40.Банк выплачивает ежегодно 5% годовых (сложный процент). Определить: а) размер вклада через 3 года, если первоначальный вклад составил 10 тыс. руб.;
б) размер первоначального вклада, при котором через 4 года вклад (вместе с процентными деньгами) составит 10000 руб.
Указание. Размер вклада 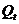 через
через 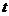 лет определяется по формуле
лет определяется по формуле 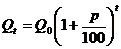 , где
, где 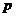 - процентная ставка за год,
- процентная ставка за год, 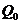 - первоначальный вклад.
- первоначальный вклад.
Краткая теория
1. Если по некоторому закону каждому натуральному числу п поставлено в соответствие определенное число ап, то говорят, что задана числовая последовательность {ап}.
2. Число А называется пределом числовой последовательности {ап}, если для любого e > 0 найдется такой номер N, зависящий от e, что для всех членов последовательности с номерами п > N верно неравенство 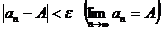 .
.
3. Число А называется пределом функции у = f(х) при х ® ¥, если для любого
e > 0 найдется также число S > 0, зависящее от e, что для всех х таких, что |х| > S будет верно неравенство  .
.
4. Число А называется пределом функции f(х) при х ® x0 , если для любого e > 0 найдется число d > 0, зависящее от e, что для все х ≠ x0 и удовлетворяющих условию
|x – x0| < d выполняется неравенство 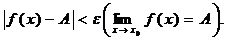
5. Функция a(х) называется бесконечно малой величиной при х ® x0 (или
х ® ¥), если 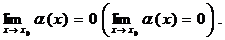
6. Функция f(x) называется бесконечно большой величиной при х ® x0 , если для любого М > 0 найдется такое число d > 0, зависящее от М, что для всех х ≠ x0 и удовлетворяющих условию |x – x0| < d будет верно неравенство 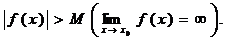
7. Свойства бесконечно малых. Если a(х) и b(х) — бесконечно малые величины при х ® x0 (или х ® ¥), то будут бесконечно малыми величины: a(х) ± b(х); с × a(х),
с – постоянная; f(x)× a(х) (f(x) – ограниченная функция); a(х) × b(х); 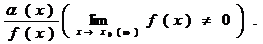
8. Свойства бесконечно больших. Если f(x) и j(х) – бесконечно большие величины при х ® x0 (или х ® ¥), то будут бесконечно большими величинами: 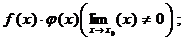
 f(x) + j(х) (j(х) — ограниченная функция); f(x)/j(х) (j(х) имеет предел).
f(x) + j(х) (j(х) — ограниченная функция); f(x)/j(х) (j(х) имеет предел).
9. Если функция a(х) есть бесконечно малая величина при х ® x0 (или х ® ¥), то функция 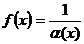 является бесконечно большой, и обратно, если f(x) бесконечно большая функция при х ® x0 (х ® ¥) , то
является бесконечно большой, и обратно, если f(x) бесконечно большая функция при х ® x0 (х ® ¥) , то 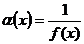 является бесконечно малой величиной.
является бесконечно малой величиной.
10. Сравнение порядков бесконечно малых. Если a(х) и b(х) — бесконечно малые величины при х ® x0 (х ® ¥) и 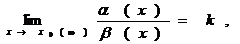 то при k = 0 бесконечно малая a(х) называется бесконечно малой более высокого порядка малости, чем b(х); при 0 < k < ¥ — одного порядка малости; при k = ¥ — более низкого порядка малости, чем b(х).
то при k = 0 бесконечно малая a(х) называется бесконечно малой более высокого порядка малости, чем b(х); при 0 < k < ¥ — одного порядка малости; при k = ¥ — более низкого порядка малости, чем b(х).
 Если k = 1, то бесконечно малые a(х) и b(х) называются эквивалентными: a(х) ~b(х).
Если k = 1, то бесконечно малые a(х) и b(х) называются эквивалентными: a(х) ~b(х).
11. Примеры эквивалентных бесконечно малых величин при х ® 0: sin x ~ x; ln(1+x) ~ x; (1 + x) m ~ 1+ mx; arcsin x ~ x; arctg x ~ x; 1 – cos x ~ x2/2.
12. Предел отношения двух бесконечно малых величин не изменится, если эти бесконечно малые заменить им эквивалентными.
13. Теоремы о пределах:
1) 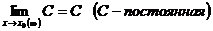 .
.
2) Если 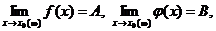
то: 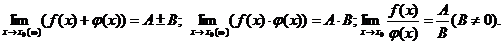
14. Если 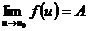 ,
, 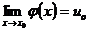 , то
, то 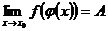 .
.
15. Первый замечательный предел: 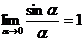
16. Второй замечательный предел (число е): 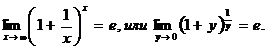
6.1. Определение предела. Простейшие пределы
Для того чтобы найти предел элементарной функции, когда аргумент стремится к значению, принадлежащему области определения этой функции, нужно в выражение функции вместо аргумента подставить его предельное значение.
6.4. Найти 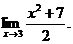
Решение. Подставляем вместо х в выражение под знаком предела 3, получим
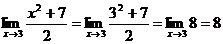 .
.
6.5. Найти 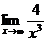 .
.
Решение. Знаменатель дроби х3 при х ® ¥ является бесконечно большой величиной, 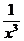 при х ® ¥ является бесконечно малой величиной, следовательно, искомый предел равен нулю.
при х ® ¥ является бесконечно малой величиной, следовательно, искомый предел равен нулю.
6.6. Найти 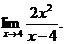
Решение. Знаменатель дроби (х — 4) при х ® 4 является бесконечно малой величиной, тогда 1/(х – 4) – бесконечно большая величина; числитель дроби 2х2 является функцией, предел которой отличен от нуля 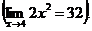
Функция 2х2/(х – 4) является бесконечно большой величиной, т.е. искомый предел равен ¥.
6.2. Раскрытие неопределенностей различных типов
Далеко не всякая подстановка предельного значения в функцию вместо независимой переменной может сразу привести к нахождению предела. Случаи, в которых подстановка предельного значения в функцию не дает значения предела, называют неопределенностями; к ним относятся неопределенности видов
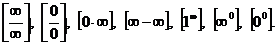
Устранить неопределенность удается часто с помощью алгебраических преобразований.
6.12. Найти 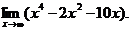
Решение. Имеем неопределенность вида [¥ – ¥]. Вынесем за скобку х в наибольшей степени: 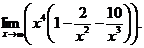
х4 является бесконечно большой величиной при х ® ¥. По теоремам о пределах
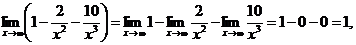
так как 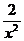 и
и 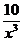 при х ® ¥ являются бесконечно малыми величинами, а предел постоянной равен самой постоянной (единице). По свойству бесконечно больших
при х ® ¥ являются бесконечно малыми величинами, а предел постоянной равен самой постоянной (единице). По свойству бесконечно больших 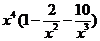 является бесконечно большой величиной, т.е. искомый предел равен ¥.
является бесконечно большой величиной, т.е. искомый предел равен ¥.
Ответ данной задачи и приведенные в решении выкладки будем использовать при решении следующих примеров как заранее известные факты. Рассмотрим несколько типов примеров, классифицируя их по виду неопределенности и предельному значению х.
1-й тип. Рассмотрим примеры вида 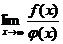 с неопределенностью вида
с неопределенностью вида 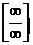 , где f(x) и j(х) в общем случае – сложные степенные или показательные функции. В случае степенных функций необходимо выносить за скобку в числителе и знаменателе дроби х с наибольшим показателем степени среди всех слагаемых дроби; в случае показательных функций за скобку выносится наиболее быстро возрастающее слагаемое среди всех слагаемых дроби. После сокращения дроби неопределенность устраняется.
, где f(x) и j(х) в общем случае – сложные степенные или показательные функции. В случае степенных функций необходимо выносить за скобку в числителе и знаменателе дроби х с наибольшим показателем степени среди всех слагаемых дроби; в случае показательных функций за скобку выносится наиболее быстро возрастающее слагаемое среди всех слагаемых дроби. После сокращения дроби неопределенность устраняется.
6.13. Найти 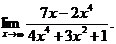
Решение. 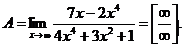 Вынося за скобку и в числителе и в знаменателе х в наибольшей степени, получим
Вынося за скобку и в числителе и в знаменателе х в наибольшей степени, получим
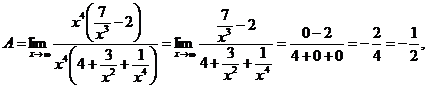
так как 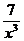 ,
, 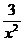 ,
, 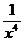 , – величины бесконечно малые при х ® ¥.
, – величины бесконечно малые при х ® ¥.
6.17.Найти 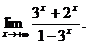
Решение. При 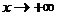 показательная функция
показательная функция 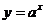 , при
, при 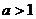 стремится к
стремится к 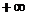 . Быстрее будет возрастать та функция, у которой основание больше, поэтому в нашем случае выносим за скобки
. Быстрее будет возрастать та функция, у которой основание больше, поэтому в нашем случае выносим за скобки 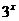 :
:
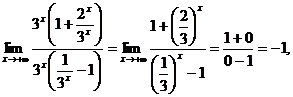
так как при 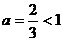
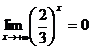 и при
и при 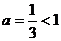
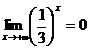 .
.
Найти пределы:
6.18. 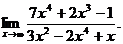
6.19. 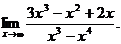
6.20. 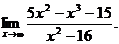
6.21. 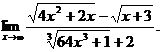
6.22. 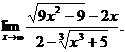
6.23. 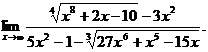
6.24. 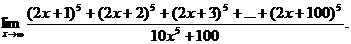
6.25. 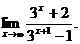
6.26. 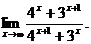
2-й тип.Рассмотрим примеры вида 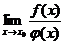 с неопределенностью вида
с неопределенностью вида 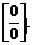 В этом случае необходимо разложить на множители и числитель, и знаменатель дроби или домножить и числитель, и знаменатель дроби на одно и то же выражение, приводящее к формулам сокращенного умножения. Неопределенность устраняется после сокращения дроби.
В этом случае необходимо разложить на множители и числитель, и знаменатель дроби или домножить и числитель, и знаменатель дроби на одно и то же выражение, приводящее к формулам сокращенного умножения. Неопределенность устраняется после сокращения дроби.
6.45. Найти 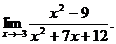
Решение. Имеем неопределенность вида 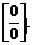 Разложим числитель и знаменатель дроби на множители: числитель – по формуле сокращенного умножения
Разложим числитель и знаменатель дроби на множители: числитель – по формуле сокращенного умножения 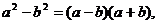 а знаменатель – по формуле разложения квадратного трехчлена на множители при
а знаменатель – по формуле разложения квадратного трехчлена на множители при 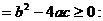
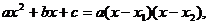 где
где 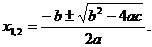
Получим 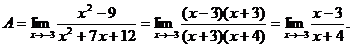
После сокращения дроби следует подставить предельное значение х в сокращенную дробь. Получим 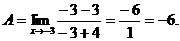
6.46. Найти 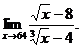
Решение. 1-й способ. Имеем неопределенность вида 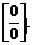 Дополним числитель до разности квадратов
Дополним числитель до разности квадратов 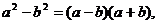 а знаменатель до разности кубов
а знаменатель до разности кубов 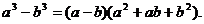 Получим
Получим 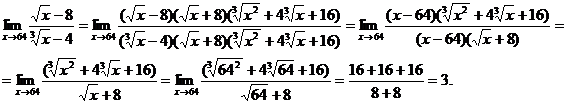
2-й способ. Сделаем замену переменной: 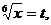 тогда
тогда 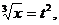 а
а 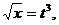 при
при 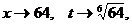 т.е.
т.е. 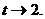 Теперь
Теперь
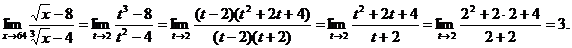
Найти пределы:
6.47. 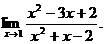
6.48. 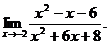
6.49. 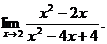
6.50. 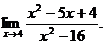
6.51. 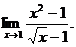
6.52. 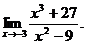
6.53. 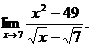
6.54. 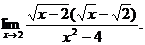
6.55. 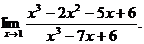
6.56. 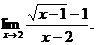
6.57. 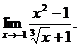
6.58. 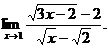
3-й тип.Рассмотрим примеры с неопределенностью вида [∞ – ∞]. Если функция, стоящая под знаком предела, представляет собой алгебраическую сумму дробей, то неопределенность устраняется или приводится ко 2-му типу после приведения дробей к общему знаменателю. Если упомянутая функция представляет собой алгебраическую сумму иррациональных выражений, то неопределенность или устраняется, или приводится к 1-му типу путем домножения и деления функции на одно и то же (сопряженное) выражение, приводящее к формулам сокращенного умножения.
6.68. Найти 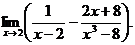
Решение. Имеем неопределенность вида [∞ – ∞]. Приведем дроби к общему знаменателю:
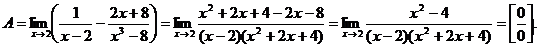
Имеем предел 2-го типа, необходимо разложить на множители числитель дроби. Получим
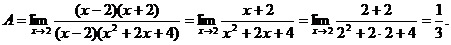
6.69. Найти 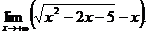
Решение. Имеем неопределенность вида [∞ – ∞]. Домножим и разделим функцию, стоящую под знаком предела на сопряженное выражение, приводящее к разности квадратов:
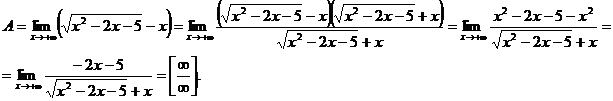
Имеем предел 1-го типа.
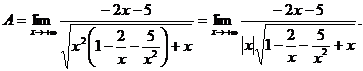
При 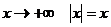 по определению модуля; поэтому
по определению модуля; поэтому
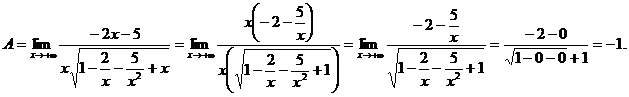
так как при 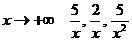 - бесконечно малые величины.
- бесконечно малые величины.
Найти пределы:
6.70. 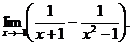
6.71. 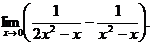
6.72. 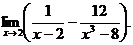
6.73. 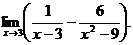
6.74. 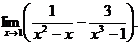
6.75. 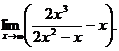
6.76. 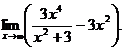
6.77. 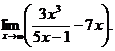
6.78. 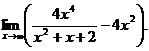
6.79. 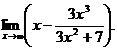
6.80. 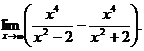
6.81. 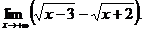
6.82. 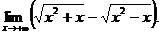
6.83. 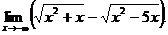
6.84. 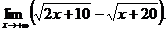
6.85. 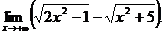
6.86. 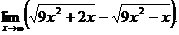
6.87. 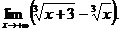
6.3. Замечательные пределы
К пределам 4-го типа отнесем примеры с неопределенностью вида 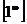 . В этом случае выражение, стоящее под знаком предела, представляет собой степенно-показательную функцию, в основании которой необходимо выделить целую часть дроби (которая должна быть равна 1). Неопределенность устраняется при помощи выделения «второго замечательного предела» .
. В этом случае выражение, стоящее под знаком предела, представляет собой степенно-показательную функцию, в основании которой необходимо выделить целую часть дроби (которая должна быть равна 1). Неопределенность устраняется при помощи выделения «второго замечательного предела» .
6.97. Найти 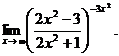
Решение. Имеем неопределенность вида  , так как
, так как
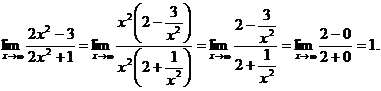
Выделим целую часть дроби 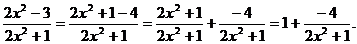
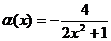 является бесконечно малой величиной при х → ∞. Домножим показатель степени на
является бесконечно малой величиной при х → ∞. Домножим показатель степени на 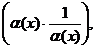 это действие не нарушает знака равенства:
это действие не нарушает знака равенства:
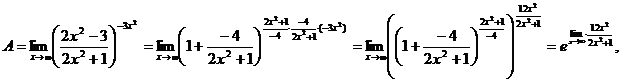
ибо 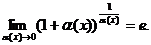 Найдем
Найдем 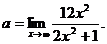 Имеем неопределенность вида
Имеем неопределенность вида 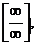 предел 1-го типа. Вынесем за скобки х2, так как вторая степень наибольшая:
предел 1-го типа. Вынесем за скобки х2, так как вторая степень наибольшая:
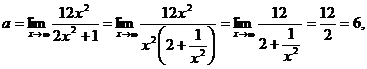
так как 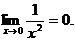 Таким образом предел равен
Таким образом предел равен 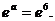
6.99. Найти 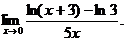
Решение. Имеем неопределенность вида 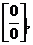 преобразуем ее в неопределенность вида
преобразуем ее в неопределенность вида 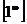 , пользуясь свойствами логарифмов:
, пользуясь свойствами логарифмов:
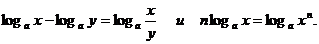
Получим 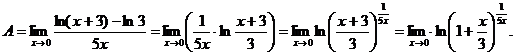
Учитывая непрерывность логарифмической функции, символы lim и ln можно переставить , получим
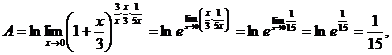
так как по формуле 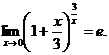
Найти пределы:
6.100. 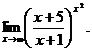
6.101. 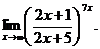
6.102. 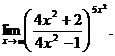
6.103. 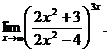
6.104. 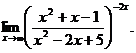
6.105. 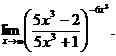
6.106. 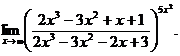
6.107. 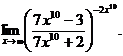
6.108. 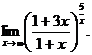
5-й тип. К этому типу отнесем функции, сводящиеся к первому замечательному пределу (6.1): 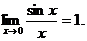
6.121. Найти 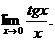
Решение. 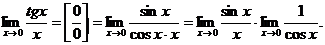
Первый сомножитель представляет собой первый замечательный предел и равен 1, второй сомножитель представляет предел, равный 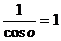 . Таким образом, искомый предел равен 1×1 = 1.
. Таким образом, искомый предел равен 1×1 = 1.
6.122. Найти 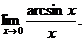
Решение. Имеем неопределенность вида 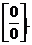 Сделаем замену переменной:
Сделаем замену переменной:
arcsin х = у; тогда х = sin у; при х → 0, у →0; получим 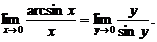
Имеем первый замечательный предел, следовательно искомый предел равен 1, что и требовалось доказать.
Найти пределы:
6.124. 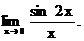
6.125. 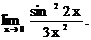
6.126. 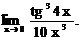
6.127. 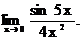
6.128. 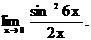
6.129. 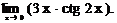
6.130. 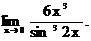
6.131. 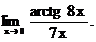
6.132. 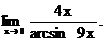
6.133. 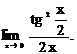
6.134. 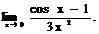
6.135. 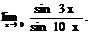
He рассмотренные в этой главе неопределенности видов [0×¥], [0°] и [¥°] могут быть устранены при помощи правила Лопиталя, которое будет рассмотрено в главе 8.
6.5. Непрерывность функции и точки разрыва.
Краткая теория
1. Функция 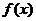 называется непрерывной в точке x0, если она удовлетворяет следующим условиям: 1) определена в точке x0; 2) имеет конечный предел при х→ x0;
называется непрерывной в точке x0, если она удовлетворяет следующим условиям: 1) определена в точке x0; 2) имеет конечный предел при х→ x0;
3) этот предел равен значению функции в этой точке: 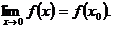 (6.1)
(6.1)
(первое определение).
2.Функция 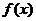 называется непрерывной в точке x0, если она определена в этой точке и бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции:
называется непрерывной в точке x0, если она определена в этой точке и бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции: 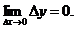 (6.2)
(6.2)
(второе определение).
3.Если функции 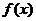 и
и 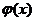 непрерывны в точке, то их сумма, произведение и частное (при условии, что знаменатель отличен от нуля) являются функциями, непрерывными в этой точке.
непрерывны в точке, то их сумма, произведение и частное (при условии, что знаменатель отличен от нуля) являются функциями, непрерывными в этой точке.
4. Если функция у = 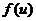 непрерывна в точке u0 =
непрерывна в точке u0 = 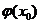 , а функция u=
, а функция u= 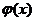 непрерывна в точке x0, то сложная функция у =
непрерывна в точке x0, то сложная функция у = 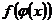 непрерывна в точке x0.
непрерывна в точке x0.
5. Функция называется непрерывной на некотором промежутке, если она непрерывна в каждой точке этого промежутка. Все элементарные функции непрерывны во всех точках, где они определены.
6. Если не выполнено определение непрерывности (6.1) или (6.2), то функция в точке x0 терпит разрыв, причем:
а) если хотя бы один из односторонних пределов
