Осташковский электромеханический техникум

Осташковский электромеханический техникум

Методическое пособие по выполнению практических работ

по дисциплине

«Теория вероятностей и математическая статистика»

Осташков 2010 г.

Рассмотрена на заседании предметной комиссии общепрофессиональных и специальных дисциплин по специальности 230105   « ____» ноября 2010 г.   Председатель комиссии:   ____________ Суркова М.В.	«У Т В Е Р Ж Д А Ю»   Заместитель директора по учебной работе     « ____» ноября 2010 г.   _____________ Осипенко С.Е.
Составлена в соответствии с Государственными требованиями к минимуму содержания и уровню подготовки выпускника для специальности №23105 «Программное обеспечение автоматизированных систем и вычислительной техники»

Автор:_____________ Суркова М.В., преподаватель ОЭМТ

Рецензенты:

Содержание.

Пояснительная записка. 4

Практическая работа №1: «Решение задач по алгебре событий». 6

Практическая работа №2: «Решение задач по комбинаторике». 8

Практическая работа №3 «Вычисление вероятностей событий по классической формуле определения вероятностей». 9

Практическая работа №4 «Решение задач на сложение и умножение вероятностей». 10

Практическая работа №5 «Решение задач по формуле полной вероятности событий и по формуле Байеса». 12

Практическая работа №6 «Решение задач на законы распределения вероятностей дискретных случайных величин». 14

Практическая работа №7 «Нахождение числовых характеристик дискретных случайных величин». 15

Практическая работа №8 «Вычисление функции и плотности распределения непрерывных случайных величин». 17

Практическая работа №9 «Вычисление числовых характеристик важнейших непрерывных распределений». 20

Практическая работа №10 «Вычисление плотности распределения одного случайного аргумента». 21

Практическая работа №11 «Построение графических изображений выборок и эмпирических функций распределения». 23

Практическая работа №12 «Вычисление выборочных средней и дисперсии». 25

Практическая работа №13 «Решение задач на доверительный интервал». 29

Практическая работа №14 «Расчёт сводных характеристик выборки методом произведений». 30

Практическая работа №15 «Расчёт сводных характеристик выборки методом сумм». 31

Самостоятельная работа. 34

Литература. 38

Пояснительная записка.

Учебная дисциплина "Теория вероятностей и математическая статистика" – это математическая наука, изучающая закономерности в случайных явлениях.

Во всех случаях, когда применяются вероятностные методы исследования, их цель состоит в том, чтобы, минуя слишком сложное изучение отдельного явления, обусловленного очень большим количеством факторов, обратиться непосредственно к законам, управляющим массами случайных явлений. Изучение этих законов позволяет не только осуществить научный прогноз в своеобразной области случайных явлений, но в ряде случаев помогает целенаправленно влиять на ход случайных явлений, контролировать их, ограничивать сферу действий случайности.

Вероятностный метод в науке не противопоставляет себя классическому методу точных наук, а является его дополнением, позволяющим глубже анализировать явление с учётом присущих ему элементов случайности.

Характерным для современного этапа развития любой науки является широкое и плодотворное применение вероятностных и статистических методов. Это вполне естественно, так как при углублённом изучении любого круга явлений неизбежно наступает этап, когда требуется не только выявление основных закономерностей, но и анализ возможных отклонений от них. В одних науках, в силу специфики предмета и исторических условий, внедрение вероятностных и статистических методов наблюдается раньше, в других – позже. В настоящее время нет почти ни одной науки, в которой так или иначе не применялись бы вероятностные и статистические методы.

Математические законы теории вероятностей – отражение реальных статистических законов, объективно существующих в массовых случайных явлениях природы. К изучению этих явлений теория вероятностей применяет математический метод и по своему методу является одним из разделов математики, столь же логически точным и строгим, как и другие математические науки.

В соответствии с учебным планом техникума на дисциплину "Теория вероятностей и математическая статистика" отводится 76 часов, в том числе 30 часов практических работ.

Решение задач по теории вероятностей и математической статистике у студентов техникума часто сопряжено со многими трудностями. Помочь студенту преодолевать эти трудности, научить применять теоретические знания к решению задач по всем разделам курса теории вероятностей и математической статистики – основное назначение данного пособия.

Известно, что при самостоятельном решении задач многие студенты нуждаются в постоянных консультациях по приёмам и методам их решения, так как найти путь к решению задачи без помощи преподавателя или соответствующего пособия студенту не под силу. Такие консультации студент может получить в данном пособии.

По теме каждой практической работы приводятся основные определения и формулы и задачи с решением.

В пособии также приведены задания для выполнения семестровой самостоятельной внеаудиторной работы студентов.

Формула Байеса.

Предположим, что выполняются условия предыдущего пункта и дополнительно известно, что событие А произошло. Найдём вероятность того, что при этом была реализована гипотеза H_k. По определению условной вероятности

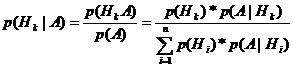
Полученное соотношение - это формула Байеса. Она позволяет по известным (до проведения опыта) p(H_i) и условным вероятностям p(A|H_i) определить условную вероятность p(H_i/А), которую называют апостериорной (то есть полученной при условии, что в результате опыта событие А уже произошло).

Пример 3.30% пациентов, поступивших в больницу, принадлежат первой социальной группе, 20% - второй и 50% - третьей. Вероятность заболевания туберкулёзом для представителя каждой социальной группы соответственно равна 0,02, 0,03 и 0,01. Проведённые анализы для случайно выбранного пациента показали наличие туберкулёза. Найти вероятность того, что это представитель третьей группы.

Решение.Пусть H₁, H₂, H₃ – гипотезы, заключающиеся в том, что пациент принадлежит соответственно первой, второй и третьей группам. Очевидно, что они образуют полную группу событий, причём p(H₁)=0,3; p(H₂)=0,2; p(H₃)=0,5. По условию событие А, обнаружение туберкулёза у больного, произошло, причём условные вероятности по данным условия равны p(А/H₁)=0,02; p(А/H₂)=0,03; и p(А/H₃)=0,01. Апостериорную вероятность p(H₃/А) вычисляем по формуле Байеса:

_.

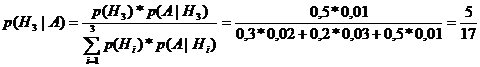Решение.

Зная F(x), можно найти плотность вероятности по формуле:

f(x)=F'(x)=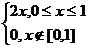

Равномерное распределение. Случайная величина х называется равномерно распределённой на [a, b], если её плотность распределения f(x) на [a, b] постоянна, а вне [a, b] равна 0:

,

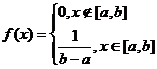Пример 1.Время ожидания автобуса (х) измеряется в минутах и распределено равномерно на отрезке [0, 30]. Определить, что ждать придётся не более 10 минут.

Решение.

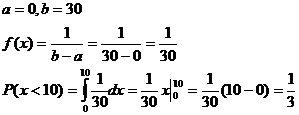
Пример 2.Задана плотность распределения: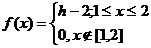

Найти h.

Решение.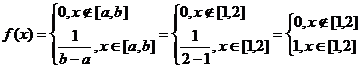

h-2=1 Þ h=3

Нормальное распределение. Случайная величина х называется нормально распределённой, если её плотность распределения f(x) имеет вид:

,

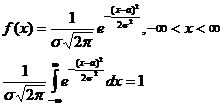где а и σ – параметры нормального распределения, σ >0.

В этом случае говорят, что х распределено нормально согласно закону N(a, σ).

Если а=0 и σ=1, то 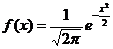и эта функция обозначается через φ(х) и называется плотностью нормированного и центрированного нормального распределения. Функция распределения в этом случае обозначается через .

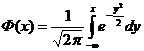Значения Ф(х) затабулированы, .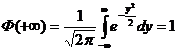

Пример.Рост мужчины в Москве имеет нормальное распределение. Средний рост мужчины в Москве а=175 см, σ=10 см. Какова вероятность, что рост первого встречного мужчины будет в пределах 160-190 см?

Решение.

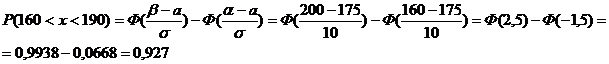
Правило трёх сигм. Случайная величина х распределена нормально N(a, σ).

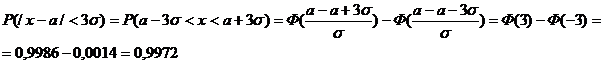
Пример.Рост мужчины в Москве имеет нормальное распределение. Средний рост мужчины в Москве а=175 см, σ=10 см. Какова вероятность, что рост первого встречного мужчины будет в пределах 145-205 см?

Решение.

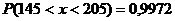
Правило двух сигм. Случайная величина х распределена нормально N(a, σ).

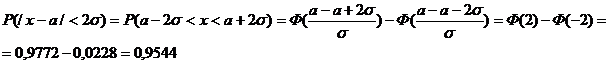
Правило одной сигмы. Случайная величина х распределена нормально N(a, σ).

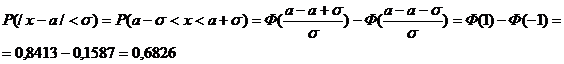
Решение.

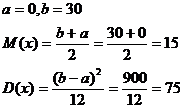
Пример.

Выработка продавцов	Число продавцов	В процентах к итогу	Кумулятивная (накопленная) численность	Накопленная относительная частота
80-100				0,1
100-120			15 (5+10)	0,3
120-140			35 (15+20)	0,7
140-160			45 (35+10)	0,9
160-180			50 (45+5)
итого

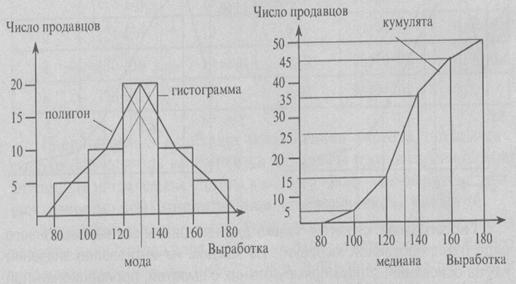
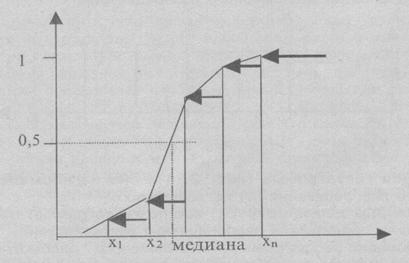
Кумулята – график накопленных частот, сглаженное графическое изображение эмпирической функции распределения. При построении кумуляты в точке, соответствующей принимаемому значению, для дискретного ряда и в правом конце интервала для интервального ряда строится перпендикуляр, высота которого пропорциональна накопленной частоте, затем верхние концы перпендикуляров соединяются между собой с помощью прямолинейных отрезков.

«Накопленные частоты» - это и есть значения эмпирической функции распределения, а кумулята – её сглаженное графическое изображение.

Самостоятельная работа.

Выполняется в виде семестрового задания. Выдаётся после изучения первых двух разделов и в оформленном виде сдаётся в конце семестра. В задание включены 12 задач по изученным темам и основным формулам теории вероятности.

Система оценки работы:

№ задачи	Набираемый балл	Шкала перевода баллов в оценки
		менее 9	2 (неуд)
		9-12	3 (удовл.)
		13-16	4 (хорошо)
		17-20	5 (отлично)
всего

Данные к задачам 1-5.

№	n	N	r	a	p1	p2	P	n	m	p
					0.7	0.9	0.9			0.2
					0.6	0.7	0.7			0.1
					0.7	0.9	0.75			0.1
					0.6	0.8	0.6			0.1
					0.7	0.8	0.65			0.2
					0.4	0.5	0.55			0.2
					0.5	0.7	0.5			0.2
					0.6	0.9	0.45			0.2
					0.6	0.5	0.4			0.1
					0.4	0.6	0.35			0.2
					0.7	0.9	0.9			0.2
					0.6	0.7	0.7			0.1
					0.7	0.9	0.75			0.1
					0.6	0.8	0.6			0.1
					0.7	0.8	0.65			0.2
					0.4	0.5	0.55			0.2
					0.5	0.7	0.5			0.2
					0.6	0.9	0.45			0.2
					0.6	0.5	0.4			0.1
					0.4	0.6	0.35			0.2
					0.7	0.9	0.9			0.2
					0.6	0.7	0.7			0.1
					0.7	0.9	0.75			0.1
					0.6	0.8	0.6			0.1
					0.7	0.8	0.65			0.2
					0.4	0.5	0.55			0.2
					0.5	0.7	0.5			0.2
					0.6	0.9	0.45			0.2
					0.6	0.5	0.4			0.1
					0.4	0.6	0.35			0.2

Данные к задачам 6-12.

№	p	N	n	m1	m2	N	p	n	N	n	m
	0.001						0.1	1 г	2 г
	0.001						0.15	2 г	4 г
	0.001						0.45	3 г	6 г
	0.001						0.25	4 г	8 г
	0.001						0.3	5 г	10 г
	0.001						0.35	6 г	12 г
	0.001						0.4	7 г	14 г
	0.001						0.45	8 г	16 г
	0.001						0.1	9 г	18 г
	0.001						0.15	10 г	20 г
	0.001						0.45	11 г	11 г
	0.001						0.25	12 г	12 г
	0.001						0.3	13 г	13 г
	0.001						0.35	14 г	14 г
	0.001						0.4	15 г	15 г
	0.001						0.1	1 г	2 г
	0.001						0.15	2 г	4 г
	0.001						0.45	3 г	6 г
	0.001						0.25	4 г	8 г
	0.001						0.3	5 г	10 г
	0.001						0.35	6 г	12 г
	0.001						0.4	7 г	14 г
	0.001						0.45	8 г	16 г
	0.001						0.1	9 г	18 г
	0.001						0.15	10 г	20 г
	0.001						0.45	11 г	11 г
	0.001						0.25	12 г	12 г
	0.001						0.3	13 г	13 г
	0.001						0.35	14 г	14 г
	0.001						0.4	15 г	15 г

Литература.

1. Богомолов Н.В. Практические занятия по математике.- М., Высшая школа, 1979.

2. Бочаров П.П., Печинкин А.В. Теория вероятностей. Математическая статистика. – М.: Гардарики, 1998.

3. Вентцель Е.С. Теория вероятностей. – М.: Высшая школа, 2001.

4. Гмурман В.Е. Теория вероятностей и математическая статистика. – М.: Высшая школа, 2001.

5. М.Р.Ефимова, Е.В.Петрова, В.Н.Румянцев. Общая теория статистики, учебник. – М., ИНФРА-М, 1999

6. В.Н.Калинина, В.Ф.Панкин. Математическая статистика. Учебник.- М., ACADEMA, 2001

7. Математика для техникумов. Алгебра и начала анализа, часть 2. Учебник под ред. Г.Н.Яковлева. – М., Наука, 1981 г.

8. Севастьянов Б.А. Курс теории вероятностей и математической статистики. – М.: Наука, 1982.

9. Солодовников А.С. Теория вероятностей. – М.: Просвещение, 1983.

Осташковский электромеханический техникум