Решение уравнений по методу хорд

Исходные данные:

- границы интервала, содержащего корень уравнения (А,В),

- R - абсолютная погрешность результата (корня уравнения),

- E - допустимое значение функции, близкое к нулю,

- Nmax - максимально допустимое число итераций.

Результаты:

- Х_n, Х_n-1 - два последних приближенных значения корня,

- f(x_n), f(x_n-1) - два последних значения функции,

- L =

Основные шаги алгоритма:

а) вычислить f(A), f(B);

б) если f(A) 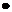f(B) > 0, то корень отсутствует, L = -1, конец работы,

в) вычислить значение абсциссы точки пересечения хорды с осью 0Х

х1 = A - f(A) 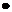(B-A)/[f(B) - f(A)];

г) если f(A) 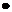f(Х1) > 0, то А = х1, f(A)=f(х1), иначе В=х1, f(В)=f(х1);

д) если f(х1) < E, то L =1, конец работы;

е) если |B - A|<=R, то L=0, конец работы, иначе перейти к пункту в).

В конце работы выполнить вывод результатов.

Необходимо также считать число итераций n и сравнивать с N_max; если n >= N_max, то закончить работу.

Решение уравнений по методу деления пополам (дихотомии)

Исходные данные и результаты те же, что в предыдущем случае.

Основные шаги алгоритма:

а) вычислить f(A), f(B);

б) если f(A) 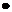f(B) > 0, то корень отсутствует, конец работы;

в) вычислить координату средины интервала х1 = 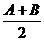и значение функции при х1: f(х1);

г) если f(A) 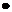f(х1) > 0, то А = х1, f(A) = f(х1), иначе В = х1, f(В) = f(х1);

д) если f(х1) < E, то конец работы,

е) если |B - A| <= R, то конец работы, иначе перейти к пункту в).

В конце работы выполнить вывод результатов. Необходимо также считать число итераций n и сравнивать с N_max; если n >= N_max, то закончить работу.

5.6 Решение уравнений по методу касательных (Ньютона)

Предварительно следует найти первую производную f ' (x).

Исходные данные и результаты те же, что в предыдущих случаях.

Основные шаги алгоритма:

а) вычислить f(A), f (B);

б) если f(A) 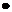f(B) > 0, то корень отсутствует, L = -1, конец работы;

в) вычислить координату пересечения касательной к графику функции с осью ОХ: x1= 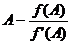A и значение функции в этой точке f(x1);

д) если f(x1) <= E, то L = 1 и конец работы;

г) если |х1-A| < R, то L = 0, конец работы, иначе A = x1, переход к пункту в).

В конце работы выполнить вывод результатов.

Необходимо также считать число итераций n и сравнивать с N_max; если n >= N_max, то закончить работу.

Методы приближённого вычисления значений интегралов

Метод прямоугольников

При использовании метода прямоугольников (рис. 1) для вычисления суммы S1 используются формулы:

S1 = h[f(X₁) + f(X₂) + ... f(X_n)],

где X₁ = A + h/2, X₁ = X_i-1 + h.

Метод трапеций

При использовании метода трапеций (рис. 2) для вычисления суммы S₁ используются формулы:

S1 = 0.5 h {f(A) + f(B) + 2[f(X₁) + f(X₂) + ... + f(X_n-1)]},

где X₁ = A + h, X₁ = X_i-1 + h.

6.3 Метод парабол (Симпсона)

При использовании метода Симпсона для вычисления суммы S₁ используется формула:

S1 = 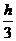{f(A) + f(B) + ... + 2[f(A+h) + f(A+3h) + ... + f(A+(n-1)h] + 4[f(A+2h) + f(A+4h) + ... + f(A+(n-2)h)]},

где n - четное число.

Для вычисления суммы S2 используются те же формулы, только при измененных значениях шага аргумента h и количества интервалов n. 4.

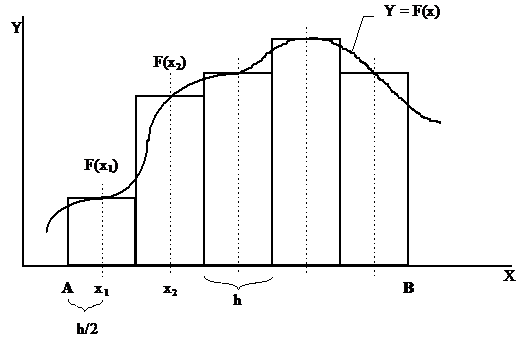
Рисунок 1

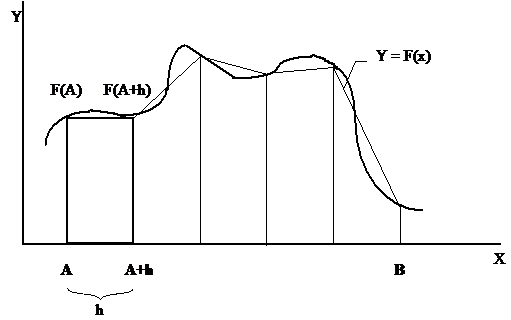
Рисунок 2

Варианты заданий для решения уравнений

№ варианта	Левая часть уравнения	Метод вычислений
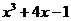		Метод итераций
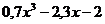		Метод половинного деления
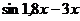		Метод хорд
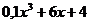		Метод касательных
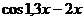		Метод итераций
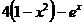		Метод половинного деления
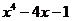		Метод хорд
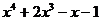		Метод касательных
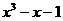		Метод итераций
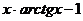		Метод половинного деления
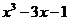		Метод хорд
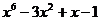		Метод касательных
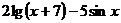		Метод итераций
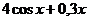		Метод половинного деления
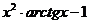		Метод хорд
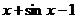		Метод касательных
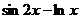		Метод итераций
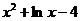		Метод половинного деления
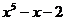		Метод хорд
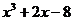		Метод касательных
	x - Sin(x)/2 – 1 = 0	Метод итераций
	2x3 + 4x – 1 = 0	Метод половинного деления
	05x – 8ln(x) - 6 = 0	Метод хорд
	x3 + 12x – 2 =	Метод касательных
	x – Sin(x) = 0.25	Метод итераций

Содержание отчета

· титульный лист;

· содержание;

· задание варианта;

· график заданной функции (функций) в Excel;

· описание заданного численного метода;

· схема программы (блок-схема алгоритма);

· листинг программы на языке Паскаль;

· полученные результаты работы программы;

· выводы.

8 Контрольные вопросы

1. Какое уравнение называется трансцендентным?

2. Какими способами можно определить интервалы корня?

3. В чем суть алгоритма решения уравнений по методу итераций?

4. В чем суть алгоритма решения уравнений по методу хорд?

5. В чем суть алгоритма решения уравнений по методу деления пополам (дихотомии)?

6. В чем суть алгоритма решения уравнений по методу касательных (Ньютона)?

7. Как учитывается абсолютная погрешность при вычислении корня?

8. Контроль каких вводимых данных необходимо осуществлять при решении трансцендентных уравнений?