Раздел 3. Аналитическая геометрия
Раздел 1: Линейная алгебра
1.1. Найти 2AB+3C, если 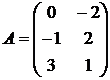 ,
, 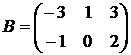 ,
, 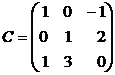 .
.
1.2. Найти 2E+AB, если 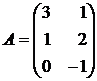 ,
, 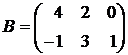 , Е – единичная матрица
, Е – единичная матрица
1.3. Найти AB+CT, если 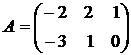 ,
, 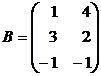 ,
, 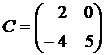
1.4. Вычислить определитель 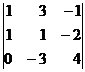
1.5. Вычислить все алгебраические дополнения элементов определителя 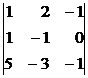
1.6. Найти обратную матрицу к матрице 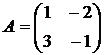 . Сделать проверку.
. Сделать проверку.
1.7. Найти обратную матрицу к матрице 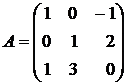 . Сделать проверку.
. Сделать проверку.
1.8. Решить систему методом Крамера и матричным методом 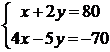
1.9. Решить систему методом Крамера и матричным методом 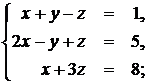
1.10. Решить систему методом Гаусса 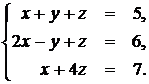
Раздел 2: Векторная алгебра
2.1. Заданы координаты векторов 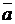 и
и 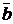 :
: 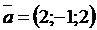 ,
, 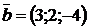 . Найти координаты вектора
. Найти координаты вектора 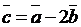 и вычислить его длину.
и вычислить его длину.
2.2. Проверить коллинеарность векторов 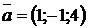 и
и 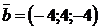
2.3. Найти координаты векторов 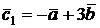 и
и 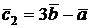 , построенных по векторам
, построенных по векторам 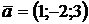 и
и 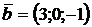 . Проверить, являются ли они коллинеарными?
. Проверить, являются ли они коллинеарными?
2.4. Найти скалярное произведение векторов 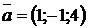 и
и 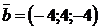 .
.
2.5. Найти координаты векторов 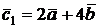 и
и 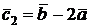 , построенных по векторам
, построенных по векторам 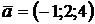 и
и 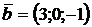 . Найти
. Найти 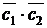 .
.
2.6. Найти угол между векторами 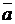 и
и 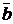 :
: 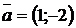 ,
, 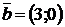
2.7. Найти угол между векторами 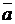 и
и 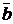 :
: 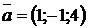 ,
, 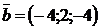
2.8. Найти векторное произведение векторов 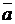 и
и 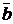 :
: 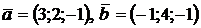
2.9. Найти площадь параллелограмма, построенного на векторах 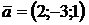 и
и 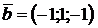 .
.
2.10. Найти площадь треугольника, построенного на векторах 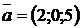 и
и 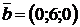 .
.
2.11. Вычислить площадь треугольника ABC: А(3;4;-1), В(2;3;0), С(-3;5;4).
2.12. Проверить, являются ли векторы 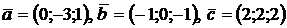 компланарными?
компланарными?
2.13. Вычислить объем параллелепипеда, построенного на векторах 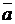 ,
, 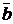 и
и 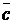 :
: 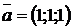 ,
, 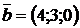 ,
, 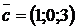 .
.
Раздел 3. Аналитическая геометрия
3.1. Даны координаты вершин треугольника: А(-1;4), В(2;-2), С(1;0). Найти:
а) длину стороны ВС б) уравнение прямой АВ
3.2. Даны координаты вершин треугольника: А(-4;2), В(2;-6), С(-10;3). Найти уравнение медианы, опущенной из вершины В (медиана делит сторону, на которую падает, пополам)
3.3. Даны координаты вершин треугольника: А(-7;4), В(7;-1), С(3;3). Найти уравнение высоты СD.
3.4. Даны координаты вершин треугольника: А(-2;2), В(1;5), С(-7;-3). Найти уравнение прямой, проходящей через точку В и параллельно АС.
3.5. Найти угол между прямыми 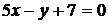 и
и 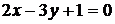 .
.
3.6. Найти расстояние от точки 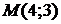 до прямой
до прямой 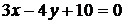 .
.
3.7. Построить кривую 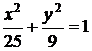 . Найти фокусы, эксцентриситет
. Найти фокусы, эксцентриситет
3.8. Построить кривую 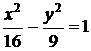 . Найти фокусы, эксцентриситет
. Найти фокусы, эксцентриситет
3.9. Даны точки: 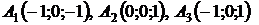 . Составить уравнение плоскости
. Составить уравнение плоскости 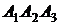 .
.
3.10. Найти угол между плоскостями 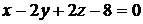 и
и 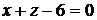 .
.
3.11. Найти расстояние от точки А(1;-2;3) до плоскости 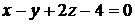 .
.
3.12. Даны точки: 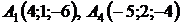 . Составить уравнение прямой
. Составить уравнение прямой 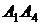 .
.
3.13. Найти угол между двумя прямыми 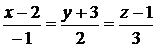 и
и 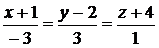 .
.
3.14. Найти точку пересечения прямой 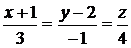 и плоскости
и плоскости 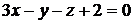 .
.
Раздел 3: Комплексные числа
4.1. Дано: 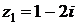 ,
, 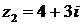 . Найти: а)
. Найти: а) 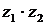 ; б)
; б) 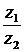 ; в)
; в) 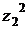 ; г)
; г) 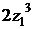 .
.
4.2. Дано: 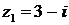 ,
, 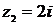 ,
, 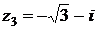 . Найти:
. Найти: 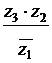 .
.
4.3. Вычислить а) 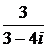 б)
б) 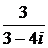 в)
в) 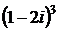
4.4. Найти модуль и аргумент комплексного числа 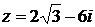 .
.
4.5. Вычилсить а) 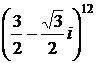 б)
б) 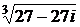 .
.
Раздел 5: Пределы и производные
Вычислить пределы:
5.1. 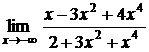 5.2.
5.2. 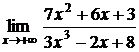 5.3.
5.3. 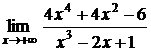
5.4. 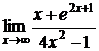 5.5.
5.5. 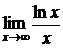 5.6.
5.6. 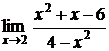
5.7. 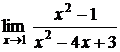 5.8.
5.8. 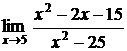 5.9.
5.9. 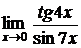
5.10. 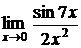 5.11.
5.11. 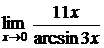 5.12.
5.12. 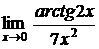
5.13. 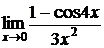 5.14.
5.14. 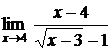 5.15.
5.15. 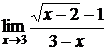
5.16. 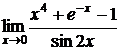 5.17.
5.17. 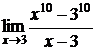 5.18.
5.18. 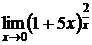
5.19. 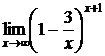
Найти производные функций:
5.20. 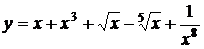 5.21.
5.21. 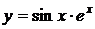 5.22.
5.22. 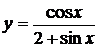
5.23. 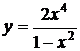 5.24.
5.24. 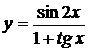 5.25.
5.25. 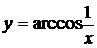
5.26. 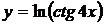 5.27.
5.27. 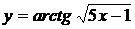 5.28.
5.28. 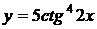
5.29.  5.30.
5.30. 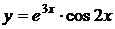 5.31.
5.31. 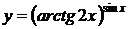
5.32. 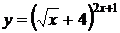
Раздел 6: Интегралы
Вычислить интегралы:
6.1. 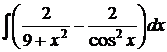 6.2.
6.2. 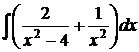
6.3. 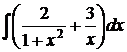 6.4.
6.4. 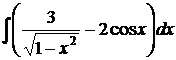
6.5. 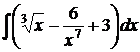 6.6.
6.6. 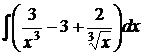 6.7.
6.7. 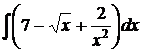
6.8. 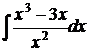 6.9.
6.9. 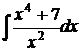 6.10.
6.10. 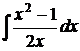
6.11. 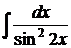 6.12.
6.12. 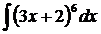 6.13.
6.13. 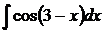
6.14. 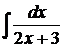 6.15.
6.15. 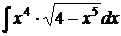 6.16.
6.16. 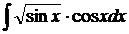
6.17. 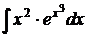 6.18.
6.18. 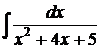 6.19
6.19 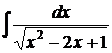
6.20. 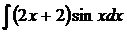 6.21.
6.21. 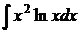 6.22.
6.22. 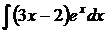
6.23. 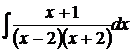 6.24.
6.24. 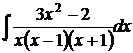 6.25.
6.25. 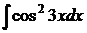
6.26. 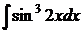 6.27.
6.27. 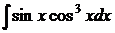
Вычислить определенные интегралы:
6.28. 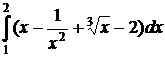 в) 6.29.
в) 6.29. 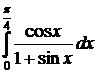
6.30 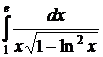 6.31.
6.31. 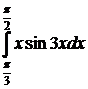 6.32.
6.32. 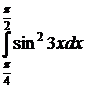
Найти площадь области, ограниченной линиями:
6.33. 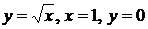 6.34.
6.34. 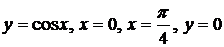
6.35. 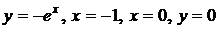 6.36.
6.36. 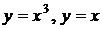
Раздел 8: Дифференциальные уравнения
Решить уравнения:
8.1. 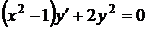 8.2.
8.2. 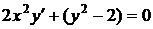
8.3. 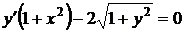 8.4.
8.4. 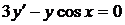
8.5. 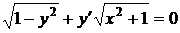 8.6.
8.6. 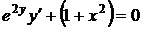
8.7. 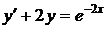 8.8.
8.8. 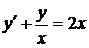
8.9. 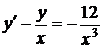 8.10.
8.10. 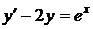
8.11. 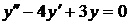 8.12.
8.12. 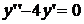
8.13. 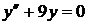 8.14.
8.14. 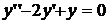
8.15. 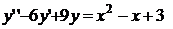 8.16.
8.16. 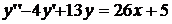
8.17. 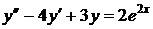 8.18.
8.18. 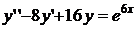
8.19. 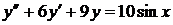 8.20.
8.20. 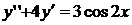
Раздел 9: Ряды
9.1. Найти сумму ряда 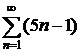 9.2. Найти сумму ряда
9.2. Найти сумму ряда 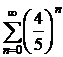
Исследовать на сходимость ряды:
9.3. 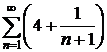 9.4.
9.4. 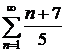 9.5.
9.5. 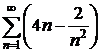
9.6. 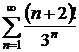 9.7.
9.7. 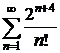 9.8.
9.8. 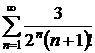
9.9. 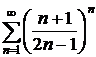 9.10.
9.10. 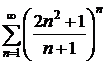 9.11.
9.11. 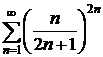
9.12. 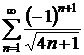 9.13.
9.13. 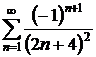 9.14.
9.14. 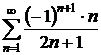
9.15. Найти радиус сходимости степенного ряда 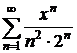 . Исследовать сходимость ряда на концах интервала. Выписать получившуюся область сходимости.
. Исследовать сходимость ряда на концах интервала. Выписать получившуюся область сходимости.
Раздел 1: Линейная алгебра
1.1. Найти 2AB+3C, если 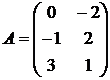 ,
, 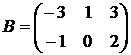 ,
, 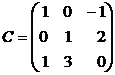 .
.
1.2. Найти 2E+AB, если 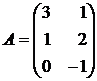 ,
, 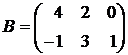 , Е – единичная матрица
, Е – единичная матрица
1.3. Найти AB+CT, если 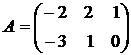 ,
, 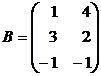 ,
, 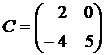
1.4. Вычислить определитель 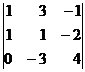
1.5. Вычислить все алгебраические дополнения элементов определителя 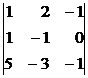
1.6. Найти обратную матрицу к матрице 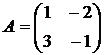 . Сделать проверку.
. Сделать проверку.
1.7. Найти обратную матрицу к матрице 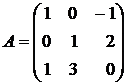 . Сделать проверку.
. Сделать проверку.
1.8. Решить систему методом Крамера и матричным методом 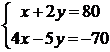
1.9. Решить систему методом Крамера и матричным методом 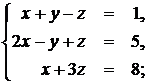
1.10. Решить систему методом Гаусса 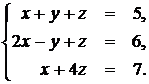
Раздел 2: Векторная алгебра
2.1. Заданы координаты векторов 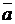 и
и 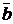 :
: 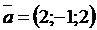 ,
, 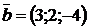 . Найти координаты вектора
. Найти координаты вектора 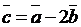 и вычислить его длину.
и вычислить его длину.
2.2. Проверить коллинеарность векторов 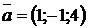 и
и 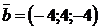
2.3. Найти координаты векторов 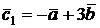 и
и 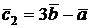 , построенных по векторам
, построенных по векторам 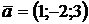 и
и 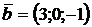 . Проверить, являются ли они коллинеарными?
. Проверить, являются ли они коллинеарными?
2.4. Найти скалярное произведение векторов 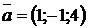 и
и 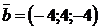 .
.
2.5. Найти координаты векторов 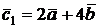 и
и 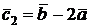 , построенных по векторам
, построенных по векторам 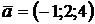 и
и 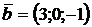 . Найти
. Найти 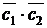 .
.
2.6. Найти угол между векторами 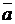 и
и 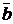 :
: 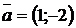 ,
, 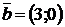
2.7. Найти угол между векторами 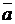 и
и 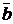 :
: 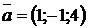 ,
, 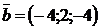
2.8. Найти векторное произведение векторов 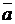 и
и 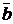 :
: 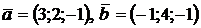
2.9. Найти площадь параллелограмма, построенного на векторах 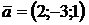 и
и 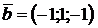 .
.
2.10. Найти площадь треугольника, построенного на векторах 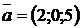 и
и 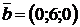 .
.
2.11. Вычислить площадь треугольника ABC: А(3;4;-1), В(2;3;0), С(-3;5;4).
2.12. Проверить, являются ли векторы 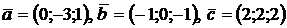 компланарными?
компланарными?
2.13. Вычислить объем параллелепипеда, построенного на векторах 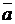 ,
, 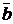 и
и 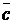 :
: 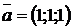 ,
, 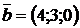 ,
, 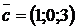 .
.
Раздел 3. Аналитическая геометрия
3.1. Даны координаты вершин треугольника: А(-1;4), В(2;-2), С(1;0). Найти:
а) длину стороны ВС б) уравнение прямой АВ
3.2. Даны координаты вершин треугольника: А(-4;2), В(2;-6), С(-10;3). Найти уравнение медианы, опущенной из вершины В (медиана делит сторону, на которую падает, пополам)
3.3. Даны координаты вершин треугольника: А(-7;4), В(7;-1), С(3;3). Найти уравнение высоты СD.
3.4. Даны координаты вершин треугольника: А(-2;2), В(1;5), С(-7;-3). Найти уравнение прямой, проходящей через точку В и параллельно АС.
3.5. Найти угол между прямыми 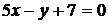 и
и 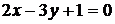 .
.
3.6. Найти расстояние от точки 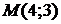 до прямой
до прямой 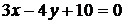 .
.
3.7. Построить кривую 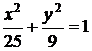 . Найти фокусы, эксцентриситет
. Найти фокусы, эксцентриситет
3.8. Построить кривую 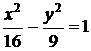 . Найти фокусы, эксцентриситет
. Найти фокусы, эксцентриситет
3.9. Даны точки: 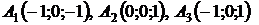 . Составить уравнение плоскости
. Составить уравнение плоскости 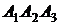 .
.
3.10. Найти угол между плоскостями 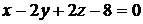 и
и 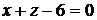 .
.
3.11. Найти расстояние от точки А(1;-2;3) до плоскости 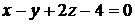 .
.
3.12. Даны точки: 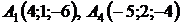 . Составить уравнение прямой
. Составить уравнение прямой 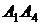 .
.
3.13. Найти угол между двумя прямыми 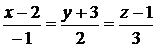 и
и 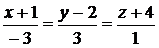 .
.
3.14. Найти точку пересечения прямой 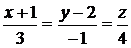 и плоскости
и плоскости 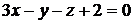 .
.
Раздел 3: Комплексные числа
4.1. Дано: 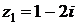 ,
, 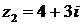 . Найти: а)
. Найти: а) 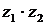 ; б)
; б) 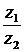 ; в)
; в) 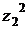 ; г)
; г) 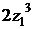 .
.
4.2. Дано: 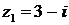 ,
, 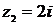 ,
, 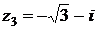 . Найти:
. Найти: 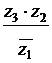 .
.
4.3. Вычислить а) 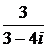 б)
б) 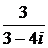 в)
в) 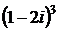
4.4. Найти модуль и аргумент комплексного числа 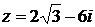 .
.
4.5. Вычилсить а) 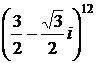 б)
б) 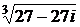 .
.
