Xii. неустановившаяся фильтрация упругой жидкости в упругой пористой среде

§ 1. Основные определения

При пуске скважин в эксплуатацию, при остановке их, при изменении темпа добычи жидкости из скважин в пласте возни­кают неустановившиеся процессы, которые проявляются в пере­распределении пластового давления (в падении или росте дав­ления вокруг скважины), в изменениях с течением времени дебитов, скоростей фильтрационных потоков и т. д.

Особенности этих неустановившихся процессов зависят от упругих свойств пластов и насыщающих их жидкостей. Хотя коэффициенты сжимаемости воды, нефти и пористой среды очень малы (b_в = 4,59×10^-10 м²/Н, b_н = (7¸30) 10^-10 м²/Н, b_с = (0,3¸2) 10^-10 м²/Н), упругость жидкостей и породы оказы­вает огромное влияние на поведение скважин и пластов в про­цессе их эксплуатации, так как объемы пласта и насыщающей его жидкости могут быть очень велики. Поэтому при подсчете запасов нефти (и газа), при проектировании разработки нефтя­ных и газовых месторождений, при эксплуатации, при исследо­вании скважин, при создании подземных хранилищ газа прихо­дится учитывать сжимаемость жидкости и пористой среды.

Объем насыщающей пласт жидкости при снижении пласто­вого давления увеличивается, а объем порового пространства уменьшается; это и определяет вытеснение жидкости из пласта в скважину (или газовую залежь).

Если в процессе разработки преобладающей формой энер­гии является энергия упругой деформации пласта и сжатой жидкости, то режим пласта называется упругим. При этом предполагается, что фильтрационный поток однофазный, т. е. пластовое давление выше давления насыщения.

В условиях упругого режима характерно то, что процесс перераспределения давления происходит медленно (длительно), а не мгновенно, как это было бы при абсолютной несжимае­мости пласта и насыщающей его жидкости.

В теории упругого режима большую роль играют два пара­метра:

I. Коэффициент упругоемкости пластагде

b^* = mb_ж + b_с (XII.1)

где т — пористость; b_ж и b_с — соответственно коэффициенты сжимаемости жидкости и пористой среды.

Коэффициент b^* численно равен изменению упругого запаса жидкости в единице объема пласта при изменении пластового давления на одну единицу. Иногда вместо коэффициента упругоемкости пласта используют приведенный модуль упругости

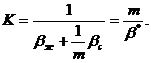(XII.2)

2.Коэффициент пьезопроводности пласта

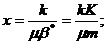(XII.3)

он характеризует темп перераспределения пластового давления в условиях упругого режима. Эта величина аналогична коэф­фициенту температуропроводности в теории теплопередачи и впервые была введена В. II. Щелкачевым.

§2. Точные решения дифференциального уравнения упругого режима

Дифференциальное уравнение упругого режима фильтрации можно записать

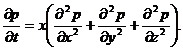(XII.4)

Интегрируя дифференциальное уравнение (XII.4) при за­данных начальном и граничных условиях, определяют давле­ние в любой точке пласта в любой момент времени.

Решение задачи перераспределения давления после пуска скважины с постоянным дебитом Q в бесконечном горизонталь­ном пласте сводится к интегрированию дифференциального уравнения (XII.4), имеющего для плоскорадиальной фильтра­ции вид

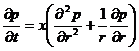(XII.5)

с начальным и граничными условиями

p(r, t) = p_к при t = 0,

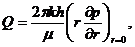(XII.6)

p(r, t) = p_к при r = .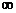

Точное решение этой задачи при г_с = 0 дается формулой

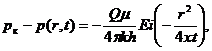(XII.7)

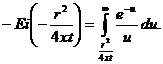(XII.8)

Эта табулированная функция называется интегральным экспоненциалом, или интегральной показательной функцией.

При малых значениях аргумента r²/4xt функцию — Ei 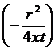можно приближенно заменить формулой

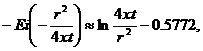(XII.9)

и тогда

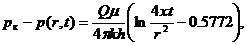(XII.10)

Формула (XII.7) является основной формулой упругого ре­жима пластов, широко применяющейся при исследовании про­цесса перераспределения пластового давления, вызванного пус­ком скважин с постоянными дебитами, остановкой скважин, изменениями темпов добычи и т. д.

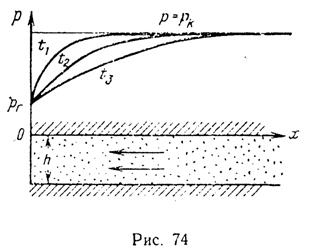
Формулу (XII.7) также можно использовать в случае при­тока жидкости к скважине конечного радиуса и в начальной стадии изменения давления в пласте конечных размеров. При неустановившейся па­раллельно-струйной фильтра­ции упругой жидкости к гале­рее, расположенной в полосообразном полубесконечном пласте перпендикулярно к оси Ох в сечении х = 0 (рис. 74) и эксплуатирующейся с постоянным давлением на за­бое галереи р_г, давление в лю­бой точке пласта в любой момент времени получим, ин­тегрируя уравнение

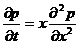(XII.11)

при начальном и граничных условиях

p(x, t) = p_к при t = 0,

p(x, t) = p_г при x = 0, (XII.12)

p(x, t) = p_к при x = ,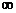

Решение выражается формулой

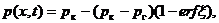(XII.13)

где

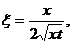
а

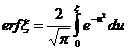. (XII.14)

—интеграл вероятности.

Подробное решение задачи о неустановившемся притоке упругой жидкости к галерее при постоянном отборе приведено ниже (см. задачу 114).

Приближенные методы решений

В связи со сложностью точных решений были предложены различные приближенные методы решения задач неустановив­шейся фильтрации упругой жидкости. Одним из наиболее рас­пространенных приближенных методов является метод последовательной смены стационарных состояний. Этот метод заклю­чается в том, что в какой-то момент времени зона пониженного давления (возмущенная зона) считается распространенной на определенное расстояние l=l(t) (приведенный радиус влияния) и предполагается, что во всей возмущенной зоне давление рас­пределяется так, как будто движение жидкости установившееся. В действительности же распределение давления в пласте не будет стационарным и зона пониженного давления захватит теоретически весь пласт. Закон изменения во времени приведен­ного радиуса влияния l(t) определяется из условия материаль­ного баланса. При неустановившемся притоке упругой жидко­сти к галерее 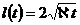, если отбор проводится при постоянной депрессии 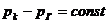; 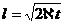, если задан постоянный дебит .

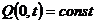При плоскорадиальном притоке упругой жидкости к скважине можно считать с точностью до 10—15%, что 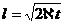(если 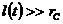) как для случая постоянной депрессии, так и для постоянного отбора.

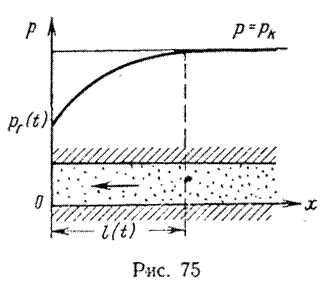В методе А. М. Пирвердяна, который развивает метод по­следовательной смены стационарных состояний, эпюра давле­ния задается так, чтобы она не имела угловых точек. Например, при притоке к галерее распределение давления по пласту за­дается в виде параболы, касательная к которой в точке x = l(t) горизонтальна (рис. 75).

Если отбор жидкости не меняется с течением времени, т. е.

то

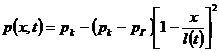(XII.15)

где

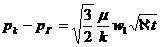(XII.16)

а приведенный радиус влияния, найденный из уравнения мате­риального баланса, определяется по формуле

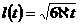(XII.17)