Найдём коэффициент детерминации.
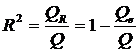
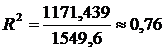
Это значит, что вариация зависимой переменной Y – дохода предприятия от продажи продукции на 76% объясняется изменчивостью объясняющей переменной Х – расходов на рекламу.
Выполним задачу №1, используя Пакет анализа программы EXCEL.
C помощью инструмента анализа данных Регрессияможно получить результаты регрессионной статистики, дисперсионного анализа, доверительных интервалов, остатки и графики подбора линии регрессии. Если в меню сервис еще нет команды Анализ данных, то необходимо сделать следующее. В главном меню последовательно выбираем Сервис→Надстройкии устанавливаем «флажок» в строке Пакет анализа (рис.1.3).
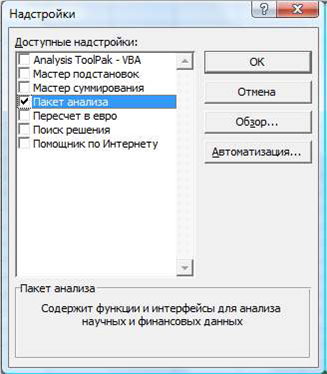
Рис. 1.3.
Ход работы:
1. Создать таблицу по исходным данным (рис 1.4.):
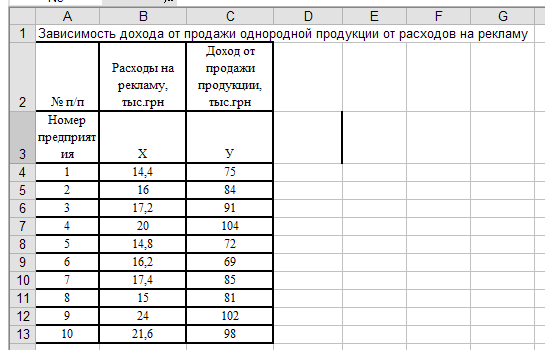
Рис. 1.4. Создание таблицы по исходным данным
2. Выполнить команду Сервис/Анализ данных
3. В диалоговом окне из списка Инструменты анализа выбрать инструмент Регрессияи нажать ОК.
4. После появления диалогового окна Регрессия(рис. 1.5.) необходимо:
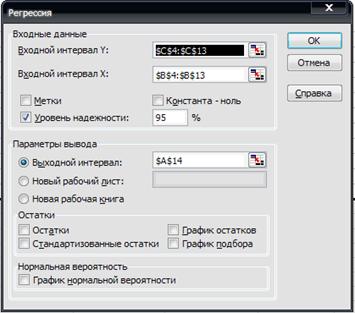
Рис. 1.5. Окно Регрессия
Здесь:
Входной интервал Y – диапазон, содержащий данные результативного признака;
Входной интервал X – диапазон, содержащий данные признака-фактора;
Метки – «флажок», который указывает, содержи ли первая строка названия столбцов;
Константа – ноль – «флажок», указывающий на наличие или отсутствие свободного члена в уравнении;
Выходной интервал – достаточно указать левую верхнюю ячейку будущего диапазона;
Новый рабочий лист – можно указать произвольное имя нового листа (или не указывать, тогда результаты выводятся на вновь созданный.
Выполнить:
1)В текстовом поле Входной интервал Yустановить диапазон ячеек зависимой переменной Y (для нашего примераС4:С13);
2)в текстовом поле Входной интервал Xустановить диапазон ячеек независимой переменной X (для нашего примераB4:B13);
3)в поле Уровень надёжности ввести необходимое число ( в примере 95, что означает уровень доверия 95%)
4)Выбрать в Параметрахвывода желаемый пункт (например, Выходной интервал С15);
5)нажатьОК.
Результаты вмещают всю необходимую информацию (рис. 1.6.):
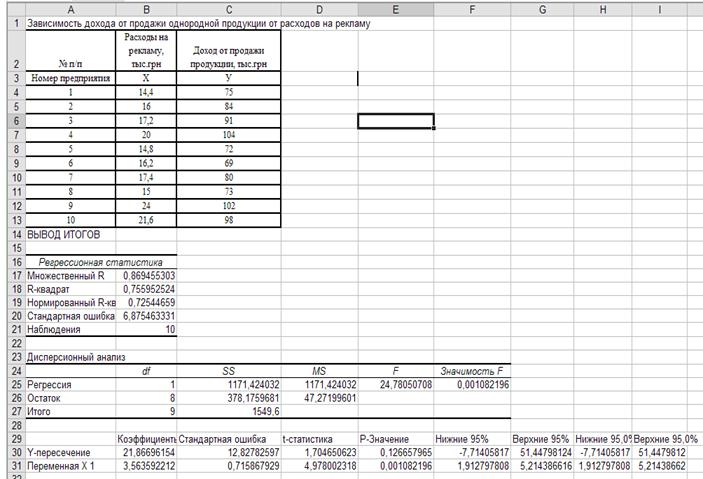
Рис. 1.6. Вывод итогов в том же окне.
В нашем отчёте:
В строке 30 в столбце «Коэффициенты» выведено значение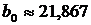 
.
В строке 31 в том же столбце выведено значение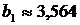 
.
В строке 17 раздела «Регрессионная статистика»выведено значение коэффициента корреляции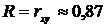 
.
В строке 18 раздела «Регрессионная статистика»выведено значение коэффициента детерминации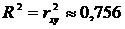 
Все показатели, вычисленные ранее, совпали.
В строке 20 раздела «Регрессионная статистика»выведено значение стандартной ошибки оценки регрессии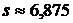 
Раздел дисперсионный анализ.
В 1 колонке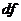 
записано число степеней свободы соответственно для компонент дисперсиирегрессии 1
Остаточной 8
Общей 9
Во 2 колонке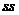 
приведенысуммы квадратов:
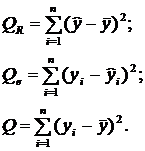
В 3 колонке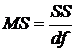 
приведены средние суммы квадратов отклонений с учётом числа степеней свободы:
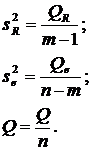
В 4 колонкеприводитсязначение F – критерия Фишера с уровнем доверия 0,95.
В 5 колонке приведена «Значимость F»,которая показывает, что при значении этого показателя менее 0,05 построенная регрессионная модель отвечает реальной регрессии.
Последняя таблица отчёта содержит:
В 1 колонке «Коэффициенты» приведены значения параметров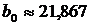 
и 
.
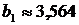Во 2 колонке «Стандартная погрешность»приведены среднеквадратические отклонения параметров модели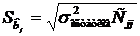 
, где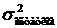 
- дисперсия остатков; Сjj-диагональный элемент матрицы погрешностей C (матрица, обратная к матрице системы нормальных уравнений).
В 3 колонке «t-статистика»приводятся стандартизованные (нормированные) параметры уравнения регрессии, которые находятся делением каждого фактически найденного параметра (1 колонка) на его стандартную погрешность (2 колонка).
В 4 колонке «Р – значения»находятся функции, которые рассчитываются по таким показателям:стандартизованные t – критерии Стьюдента, вычисленные путём деления t – критерии на значения их стандартных погрешностей; количество степеней свободы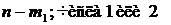 
:
если связь между Х и Y положительная или отрицательная, то используют число 1;
если не известно какой связи между Х и Yследует ожидать, то используют число 2.
В общем, если Р<0,05 то оценки параметров уравнения регрессии являются достоверными и модель отвечает реальной действительности.
В 5 колонке «Нижние 95%, Верхние 95%»помещены нижние и верхние границы 95-процентного уровня доверия для каждого параметра регрессии. Если доверительные интервалы не содержат в себе нуль, то с 95- процентной уверенностью можно утверждать, что независимая переменная добавляет в уравнение регрессии значимую информацию и можно достаточно точно описывать рассмотренный процесс или явление.
Рис. 1.7. Отчёт
Задача для самостоятельного решения №1
Получены данные о продаже товара Y млн. грн при общем объеме товарооборота X млрд. грн Построить линейную парную регрессию Yна X.
Необходимо:
1. Построить поле корреляции.
2. Рассчитать параметры парной линейной регрессии и объяснить их смысл.
3. Оцените тесноту связи с помощью показателей корреляции и детерминации.
4. Вычислить стандартную ошибку оценки регрессии.
5. Вычислить точечный прогноз реализации товара для х=х0 .
6.Найти 95% интервалы:
1) для коэффициента корреляции;
2) математического ожидания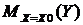 
;
3) индивидуального значения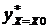 
;
4) для параметра β1 регрессионной модели;
5) для параметра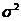 
.
7.Оценить на уровне значимости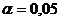 
значимость уравнения регрессии У по Х:
1) Используя F – критерий Фишера;
2) Используя t – распределение Стьюдента.
Уровень значимости принять равным α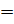 
0,05. Данные приведены в таблице 1.4.
Таблица 1.4
Варианты заданий для группы 21
| № | Данные о продаже | ||||||||||
| Х0=3,8 | Х | 2,6 | 2,8 | 2,9 | 3,0 | 3,3 | 3,6 | 3,7 | 3,9 | 3,9 | 4,0 |
| Y | 10,4 | 10,7 | 11,5 | 11,8 | 12,2 | 15,5 | 17,6 | 17,7 | 18,3 | 18,3 | |
| Х0=3,4 | Х | 3,2 | 3,3 | 3,5 | 3,7 | 3,8 | 4,0 | 4,3 | 4,5 | 4,5 | 4,7 |
| Y | 5,8 | 5,9 | 6,5 | 7,4 | 7,6 | 7,8 | 8,7 | 8,9 | 9,1 | 9,4 | |
| Х0=4,1 | Х | 3,7 | 3,9 | 4,0 | 4,2 | 4,3 | 4,6 | 4,7 | 4,9 | 5,1 | 5,2 |
| Y | 15,5 | 17,5 | 19,5 | 21,0 | 22,1 | 23,6 | 26,0 | 28,1 | 29,5 | 31,2 | |
| Х0=8 | Х | 3,0 | 3,1 | 3,2 | 3,3 | 3,6 | 3,8 | 4,0 | 4,2 | 4,3 | 4,4 |
| Y | 7,6 | 8,5 | 9,3 | 10,2 | 10,3 | 10,4 | 10,5 | 10,7 | 11,2 | 11,4 | |
| Х0=9,1 | Х | 2,4 | 2,7 | 2,9 | 3,0 | 3,6 | 4,0 | 4,4 | 4,8 | 5,0 | 5,3 |
| Y | 9,0 | 9,2 | 10,1 | 10,2 | 10,3 | 10,4 | 10,5 | 10,7 | 11,2 | 11,4 | |
| Х0=3,2 | Х | 2,5 | 2,8 | 3,0 | 3,5 | 3,7 | 4,3 | 4,6 | 5,0 | 5,2 | 5,3 |
| Y | 11,4 | 11,7 | 12,5 | 12,8 | 13,2 | 16,5 | 18,6 | 18,7 | 19,3 | 19,3 |
| Х0=4,2 | Х | 2,5 | 2,7 | 3,1 | 3,6 | 4,0 | 4,4 | 4,7 | 5,0 | 5,1 | 5,1 |
| Y | 4,3 | 4,4 | 5,0 | 5,9 | 6,1 | 6,2 | 7,2 | 7,4 | 7,6 | 7,9 | |
| Х0=3 | Х | 2,9 | 3,1 | 3,1 | 3,2 | 3,3 | 3,4 | 3,5 | 3,5 | 3,5 | 3,6 |
| Y | 16,2 | 18,3 | 18,2 | 19,0 | 19,6 | 20,3 | 21,5 | 22,5 | 23,3 | 24,1 | |
| Х0=4 | Х | 3,9 | 4,3 | 4,5 | 4,6 | 5,2 | 5,8 | 6,0 | 6,4 | 6,6 | 6,6 |
| Y | 10,6 | 11,5 | 12,3 | 13,2 | 13,4 | 14,2 | 16,0 | 17,1 | 17,8 | 18,9 | |
| Х0=4 | Х | 3,6 | 3,7 | 3,8 | 3,9 | 4,1 | 4,5 | 4,6 | 4,8 | 4,9 | 5,0 |
| Y | 12,9 | 13,2 | 14,0 | 14,3 | 14,7 | 18,0 | 18,1 | 20,2 | 20,8 | 20,8 | |
| Х0=4,1 | Х | 3,2 | 3,2 | 3,4 | 4,0 | 3,8 | 4,0 | 4,2 | 4,4 | 4,5 | 4,6 |
| Y | 11,6 | 11,9 | 12,9 | 14,7 | 15,2 | 15,5 | 17,5 | 17,8 | 18,1 | 18,8 | |
| Х0=3 | Х | 2,7 | 2,8 | 2,9 | 3,2 | 3,3 | 2,6 | 3,7 | 3,9 | 3,9 | 4,1 |
| Y | 9,2 | 10,2 | 11,2 | 12,0 | 12,6 | 13,3 | 14,5 | 15,6 | 16,3 | 17,1 | |
| Х0=4 | Х | 3,6 | 3,7 | 3,8 | 3,9 | 4,2 | 4,5 | 4,6 | 4,8 | 4,8 | 5,0 |
| Y | 10,4 | 11,3 | 12,1 | 13,0 | 13,2 | 14,0 | 15,8 | 16,9 | 17,6 | 18,7 | |
| Х0=3 | Х | 2,0 | 2,4 | 2,6 | 2,7 | 3,3 | 3,9 | 4,1 | 4,5 | 4,7 | 4,7 |
| Y | 8,0 | 8,4 | 10,1 | 10,4 | 10,6 | 10,8 | 11,0 | 11,4 | 12,4 | 12,9 | |
| Х0=4,2 | Х | 3,4 | 3,8 | 4,0 | 4,1 | 4,7 | 5,3 | 5,5 | 5,9 | 6,1 | 6,1 |
| Y | 8,6 | 9,4 | 10,2 | 11,1 | 11,3 | 12,1 | 13,9 | 15,0 | 15,7 | 16,8 | |
| Х0=4 | Х | 3,3 | 3,4 | 3,5 | 3,6 | 3,9 | 4,2 | 4,3 | 4,5 | 4,5 | 4,7 |
| Y | 12,6 | 12,9 | 13,7 | 14,0 | 14,4 | 17,7 | 17,8 | 19,9 | 20,5 | 20,5 | |
| Х0=3 | Х | 2,3 | 2,5 | 2,9 | 3,4 | 3,6 | 4,2 | 4,4 | 4,8 | 5,0 | 5,0 |
| Y | 10,1 | 10,2 | 11,2 | 13,0 | 13,4 | 13,8 | 5,8 | 16,1 | 16,4 | 19,0 | |
| Х0=6 | Х | 5,6 | 5,9 | 6,2 | 6,5 | 6,7 | 7,2 | 7,3 | 7,6 | 7,8 | 8,3 |
| Y | 8,9 | 9,0 | 9,3 | 9,6 | 10,0 | 10,1 | 10,6 | 10,9 | 11,0 | 11,6 | |
| Х0=4 | Х | 3,1 | 3,2 | 3,4 | 3,7 | 3,8 | 3,9 | 4,2 | 4,4 | 4,6 | 4,8 |
| Y | 19,8 | 20,4 | 21,9 | 22,3 | 23,4 | 30,0 | 34,1 | 34,3 | 35,3 | 35,5 | |
| Х0=8 | Х | 7,6 | 7,9 | 8,2 | 8,5 | 8,7 | 9,2 | 9,3 | 9,6 | 9,8 | 10,3 |
| Y | 2,4 | 2,5 | 2,5 | 2,6 | 2,9 | 3,5 | 4,3 | 4,4 | 4,8 | 5,1 | |
| Х0=5 | Х | 4,6 | 4,9 | 5,2 | 5,5 | 5,7 | 6,2 | 6,3 | 6,6 | 6,8 | 7,3 |
| Y | 4,1 | 4,0 | 3,7 | 3,6 | 3,4 | 3,3 | 3,2 | 3,0 | 3,0 | 2,7 |
| Х0=5 | Х | 4,1 | 4,2 | 4,4 | 4,7 | 4,8 | 4,9 | 5,2 | 5,4 | 5,6 | 5,8 |
| Y | 15,5 | 17,5 | 19,5 | 21,0 | 22,1 | 23,6 | 26,0 | 28,1 | 29,5 | 30,2 | |
| Х0=3 | Х | 2,6 | 2,9 | 3,2 | 3,5 | 3,7 | 4,2 | 4,3 | 4,6 | 4,8 | 5,3 |
| Y | 38,7 | 40,1 | 43,2 | 46,0 | 50,0 | 56,0 | 59,0 | 60,0 | 61,0 | 66,0 | |
| Х0=6 | Х | 5,1 | 5,2 | 5,4 | 5,7 | 5,8 | 5,9 | 6,2 | 6,4 | 6,6 | 6,8 |
| Y | 8,6 | 9,5 | 10,3 | 11,2 | 11,4 | 12,2 | 14,0 | 15,1 | 15,8 | 16,9 | |
| Х0=4 | Х | 3,6 | 3,9 | 4,2 | 4,5 | 4,7 | 5,2 | 5,3 | 5,6 | 5,8 | 6,3 |
| Y | 13,8 | 14,6 | 14,9 | 16,3 | 18,6 | 24,6 | 33,2 | 34,4 | 38,8 | 40,8 | |
| Х0=5 | Х | 4,9 | 5,2 | 5,5 | 5,8 | 6,0 | 6,5 | 6,6 | 6,9 | 7,1 | 7,6 |
| Y | 7,8 | 7,9 | 8,2 | 8,5 | 8,9 | 9,0 | 9,5 | 9,8 | 9,9 | 10,5 | |
| Х0=4,8 | Х | 3,5 | 3,6 | 3,8 | 4,0 | 4,3 | 4,4 | 4,6 | 4,7 | 5,0 | 5,2 |
| Y | 19,8 | 20,4 | 21,9 | 22,3 | 23,4 | 30,0 | 34,1 | 34,3 | 35,3 | 35,5 | |
| Х0=6 | Х | 5,9 | 6,2 | 6,5 | 6,8 | 7,0 | 7,5 | 7,6 | 7,9 | 8,1 | 8,6 |
| Y | 2,4 | 2,5 | 2,5 | 2,6 | 2,9 | 3,5 | 4,3 | 4,4 | 4,8 | 5,1 | |
| Х0=5 | Х | 4,4 | 4,6 | 4,8 | 5,1 | 5,3 | 5,4 | 5,6 | 5,8 | 6,0 | 6,1 |
| Y | 5,8 | 5,9 | 6,5 | 7,4 | 7,6 | 7,7 | 8,8 | 8,9 | 9,1 | 9,3 | |
| Х0=7 | Х | 6,9 | 7,2 | 7,5 | 7,8 | 8,0 | 8,5 | 8,6 | 8,9 | 9,1 | 9,6 |
| Y | 2,1 | 2,0 | 1,7 | 1,6 | 1,4 | 1,3 | 1,2 | 1,0 | 1,0 | 0,7 | |
| Х0=5 | Х | 4,5 | 4,6 | 4,8 | 5,1 | 5,3 | 5,4 | 5,5 | 5,7 | 6,0 | 6,2 |
| Y | 15,5 | 17,5 | 17,5 | 21,0 | 22,1 | 23,6 | 26,0 | 28,1 | 29,5 | 30,2 | |
| Х0=4,5 | Х | 3,5 | 3,6 | 3,8 | 4,0 | 4,3 | 4,4 | 4,6 | 4,7 | 5,0 | 5,2 |
| Y | 8,6 | 9,5 | 10,3 | 11,2 | 11,4 | 12,2 | 14,0 | 15,1 | 15,8 | 16,9 | |
| Х0=4 | Х | 3,9 | 4,2 | 4,5 | 4,8 | 5,0 | 5,5 | 5,6 | 5,9 | 6,1 | 6,6 |
| Y | 15,8 | 16,6 | 16,9 | 18,3 | 20,6 | 26,6 | 35,2 | 36,4 | 40,8 | 42,8 | |
| Х0=6 | Х | 5,1 | 5,5 | 5,8 | 6,1 | 6,5 | 6,7 | 7,3 | 7,6 | 8,0 | 8,3 |
| Y | 8,9 | 9,0 | 9,3 | 9,6 | 10,0 | 10,1 | 10,6 | 10,9 | 11,0 | 11,6 | |
| Х0=3,5 | Х | 3,3 | 3,6 | 3,7 | 3,9 | 4,0 | 4,1 | 4,2 | 4,4 | 4,5 | 4,6 |
| Y | 14,8 | 15,4 | 16,9 | 17,3 | 18,4 | 25,0 | 29,1 | 29,3 | 30,3 | 30,5 |
Таблица 1.5
Варианты заданий для группы 22
| № | Данные о продаже | ||||||||||
| Х0=7 | Х | 6,1 | 6,5 | 6,8 | 7,1 | 7,5 | 7,7 | 8,3 | 8,6 | 9,0 | 9,3 |
| Y | 3,4 | 3,5 | 3,5 | 3,6 | 3,9 | 4,5 | 5,3 | 5,4 | 5,8 | 6,1 | |
| Х0=4,5 | Х | 4,3 | 4,6 | 4,7 | 4,9 | 5,0 | 5,1 | 5,2 | 5,4 | 5,5 | 5,6 |
| Y | 5,8 | 5,9 | 6,5 | 7,4 | 7,6 | 7,7 | 8,8 | 8,9 | 9,0 | 9,3 | |
| Х0=7 | Х | 6,1 | 6,5 | 6,8 | 7,1 | 7,5 | 7,7 | 8,3 | 8,6 | 9,0 | 9,3 |
| Y | 5,1 | 5,0 | 4,7 | 4,6 | 4,4 | 4,3 | 4,2 | 4,0 | 4,0 | 3,7 | |
| Х0=3,8 | Х | 3,3 | 3,6 | 3,7 | 3,9 | 4,0 | 4,1 | 4,2 | 4,4 | 4,5 | 4,6 |
| Y | 13,5 | 15,5 | 17,5 | 19,0 | 20,1 | 21,6 | 24,0 | 26,1 | 27,5 | 28,2 | |
| Х0=4 | Х | 3,1 | 3,5 | 3,8 | 4,1 | 4,5 | 4,7 | 5,3 | 5,6 | 6,0 | 6,3 |
| Y | 8,6 | 9,5 | 10,3 | 11,2 | 11,4 | 12,2 | 14,0 | 15,1 | 15,8 | 16,9 | |
| Х0=3,5 | Х | 3,3 | 3,6 | 3,7 | 3,9 | 4,0 | 4,1 | 4,2 | 4,4 | 4,5 | 4,6 |
| Y | 8,6 | 9,5 | 10,3 | 11,2 | 11,4 | 12,2 | 14,0 | 15,1 | 15,8 | 16,9 | |
| Х0=4,2 | Х | 2,1 | 2,5 | 2,8 | 3,1 | 3,5 | 3,7 | 4,3 | 4,6 | 5,0 | 5,3 |
| Y | 13,8 | 14,6 | 14,9 | 16,3 | 18,6 | 20,8 | 23,2 | 24,4 | 24,6 | 28,8 | |
| Х0=5 | Х | 3,8 | 4,2 | 4,5 | 4,8 | 5,2 | 5,4 | 6,0 | 6,3 | 6,7 | 7,0 |
| Y | 8,8 | 8,9 | 9,2 | 9,5 | 9,9 | 10,0 | 10,5 | 10,8 | 10,9 | 11,5 | |
| Х0=4 | Х | 3,5 | 3,6 | 3,7 | 3,9 | 4,0 | 4,2 | 4,3 | 4,5 | 4,6 | 4,8 |
| Y | 13,8 | 14,4 | 15,9 | 16,3 | 17,4 | 24,0 | 28,1 | 28,3 | 29,5 | 39,3 | |
| Х0=6 | Х | 5,8 | 6,2 | 6,5 | 6,8 | 7,2 | 7,4 | 8,0 | 8,3 | 8,7 | 9,0 |
| Y | 4,4 | 4,5 | 4,5 | 4,6 | 4,9 | 5,5 | 6,3 | 6,4 | 6,8 | 7,1 | |
| Х0=4,1 | Х | 3,5 | 3,6 | 3,7 | 3,9 | 4,0 | 4,2 | 4,3 | 4,5 | 4,6 | 4,8 |
| Y | 5,8 | 5,9 | 6,5 | 7,4 | 7,6 | 7,7 | 8,8 | 8,9 | 9,1 | 9,3 | |
| Х0=6 | Х | 5,8 | 6,2 | 6,5 | 6,8 | 7,2 | 7,4 | 8,0 | 8,3 | 8,7 | 9,0 |
| Y | 6,1 | 6,0 | 5,7 | 5,6 | 5,4 | 5,3 | 5,2 | 5,0 | 5,0 | 4,7 | |
| Х0=4 | Х | 3,5 | 3,6 | 3,7 | 3,9 | 4,0 | 4,2 | 4,3 | 4,5 | 4,6 | 4,8 |
| Y | 13,5 | 15,5 | 17,5 | 19,0 | 20,1 | 21,6 | 24,0 | 26,1 | 27,5 | 28,2 | |
| Х0=3 | Х | 2,8 | 3,2 | 3,5 | 3,8 | 4,2 | 4,4 | 5,0 | 5,3 | 5,7 | 6,0 |
| Y | 18,7 | 20,1 | 23,2 | 26,0 | 30,0 | 36,0 | 39,0 | 40,0 | 41,0 | 46,0 | |
| Х0=4,1 | Х | 3,5 | 3,6 | 3,7 | 3,9 | 4,0 | 4,2 | 4,3 | 4,5 | 4,6 | 4,8 |
| Y | 7,6 | 8,5 | 9,3 | 10,2 | 10,4 | 11,2 | 13,0 | 14,1 | 14,8 | 15,9 |
| Х0=90 | Х | ||||||||||
| Y | |||||||||||
| Х0=9 | Х | 7,8 | 8,7 | 8,9 | 9,6 | 10,6 | 10,6 | 10,8 | 11,2 | ||
| Y | 13,3 | 13,5 | 13,8 | 14,4 | 14,7 | 14,9 | 15,3 | 15,5 | 16,4 | 16,8 | |
| Х0=100 | Х | ||||||||||
| Y | |||||||||||
| Х0=10 | Х | 8,1 | 8,3 | 9,2 | 9,9 | 10,9 | 11,1 | 12,3 | 11,5 | ||
| Y | 13,2 | 13,5 | 14,1 | 14,3 | 14,6 | 15,2 | 16,1 | 16,5 | |||
| Х0=80 | Х | ||||||||||
| Y | |||||||||||
| Х0=9 | Х | 7,6 | 7,8 | 8,5 | 8,7 | 9,4 | 10,4 | 10,6 | 10,9 | 11,1 | |
| Y | 13,1 | 13,3 | 13,6 | 14,2 | 14,5 | 14,7 | 15,1 | 15,3 | 16,2 | 16,6 | |
| Х0=80 | Х | ||||||||||
| Y | |||||||||||
| Х0=10 | Х | 7,3 | 7,5 | 8,2 | 8,4 | 9,1 | 10,1 | 10,3 | 10,6 | 10,7 | 10,8 |
| Y | 12,8 | 13,3 | 13,9 | 14,2 | 14,4 | 14,8 | 15,9 | 16,3 | |||
| Х0=70 | Х | ||||||||||
| Y | |||||||||||
| Х0=9 | Х | 6,9 | 7,1 | 7,8 | 8,7 | 9,7 | 9,9 | 10,2 | 10,3 | 10,4 | |
| Y | 12,4 | 12,6 | 12,9 | 13,5 | 13,8 | 14,4 | 14,6 | 15,5 | 15,9 | ||
| Х0=75 | Х | ||||||||||
| Y | |||||||||||
| Х0=8 | Х | 6,6 | 6,8 | 7,5 | 7,7 | 8,4 | 9,4 | 9,7 | 9,9 | 10,1 | |
| Y | 12,1 | 12,3 | 12,6 | 13,2 | 13,5 | 13,7 | 14,1 | 14,3 | 15,2 | 15,7 | |
| Х0=76 | Х | ||||||||||
| Y | |||||||||||
| Х0=7 | Х | 6,7 | 6,5 | 7,2 | 7,4 | 8,1 | 8,9 | 9,3 | 9,7 | 10,1 | 10,5 |
| Y | 11,7 | 12,1 | 12,4 | 12,8 | 13,3 | 13,5 | 13,8 | 14,1 | 14,7 | 15,2 | |
| Х0=72 | Х | ||||||||||
| Y |
| Х0=6 | Х | 5,9 | 6,1 | 6,8 | 7,0 | 7,7 | 8,5 | 8,7 | 9,3 | 9,9 | 10,2 |
| Y | 11,3 | 11,7 | 12,1 | 12,4 | 12,9 | 13,1 | 13,4 | 13,7 | 14,4 | 14,8 | |
| Х0=7 | Х | 6,1 | 6,5 | 6,8 | 7,1 | 7,5 | 7,7 | 8,3 | 8,6 | 9,0 | 9,3 |
| Y | 4,4 | 4,5 | 4,5 | 4,6 | 4,9 | 5,5 | 6,3 | 6,4 | 6,8 | 4,4 | |
| Х0=8 | Х | 6,1 | 6,5 | 6,8 | 7,1 | 7,5 | 7,7 | 8,3 | 8,6 | 9,0 | 6,1 |
| Y | 6,1 | 6,0 | 5,7 | 5,6 | 5,4 | 5,3 | 5,2 | 5,0 | 5,0 | 6,1 | |
| Х0=4 | Х | 3,5 | 3,6 | 3,8 | 4,0 | 4,3 | 4,4 | 4,6 | 4,7 | 5,0 | 5,2 |
| Y | 8,9 | 9,0 | 9,3 | 9,6 | 10,0 | 10,1 | 10,6 | 10,9 | 11,0 | 11,6 | |
| Х0=6 | Х | 5,1 | 5,5 | 5,8 | 6,1 | 6,5 | 6,7 | 7,3 | 7,6 | 8,0 | 8,3 |
| Y | 14,8 | 15,4 | 16,9 | 17,3 | 18,4 | 25,0 | 29,1 | 29,3 | 30,3 | 30,5 |