Задача Баклея - Леверетта и ее обобщения
В случае одномерного течения несжимаемых несмешивающихся жидкостей в условиях, когда можно пренебречь капиллярным давлением процесс вытеснения допускает простое математическое описание.
Для обоих случаев одномерного потока (прямолинейно-параллельного и плоскорадиального) это приводит к классической в теории вытеснения модели Баклея - Леверетта.
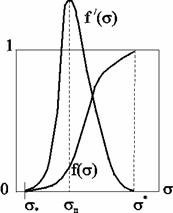
Рис. 5.8. Вид функции Баклея–Леверетта и её производной
В рассматриваемом случае важное значение имеет так называемая функция Баклея - Леверетта или функция распределения потоков фаз f(s), которая имеет простой физический смысл. Действительно, данная функция представляет собой отношение скорости фильтрации вытесняющей фазы к суммарной скорости, и равна объемной доле потока вытесняющей жидкости (воды) в суммарном потоке двух фаз. Таким образом, функция Баклея – Лаверетта определяет полноту вытеснения и характер распределения нефтегазоконденсатонасыщенности по пласту. Задачи повышения нефте- и газоконденсатоотдачи в значительной степени сводятся к применению таких воздействий на пласт, которые в конечном счете изменяют вид функции f(s) в направлении увеличения полноты вытеснения.
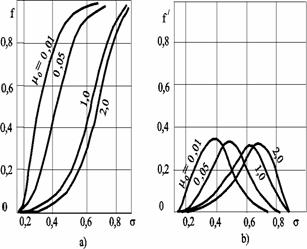
Рис. 5.9. Графики функции Баклея–Леверетта
(а) и её производной (b) для различных отношений вязкости m0
Вид кривых функции f(s) и ее производной f/(s) показан на рис.5.8. С ростом насыщенности f(s) монотонно возрастает от 0 до 1. Характерной особенностью графика f(s) является наличие точки перегиба sп , участков вогнутости и выпуклости, где вторая производная f//(s), соответственно, больше и меньше нуля. Эта особенность в большой степени определяет специфику фильтрационных задач вытеснения в рамках модели Баклея – Леверетта.
Зависимость функций f(s) и f/(s) от отношения вязкостей фаз m0=m1/ m2 показана рис. 5.9. Из данного рисунка следует, что с ростом отношения вязкостей кривая f(s) сдвигается вправо и эффективность вытеснения возрастает. Например, применение пен и загустителей, повышающих вязкость нагнетаемой воды, может значительно увеличить нефтеотдачу.
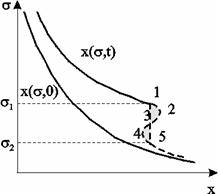
Рис. 5.10. Устранение многозначности распределения насыщенности введением скачка
Физической особенностью модели двухфазного вытеснения Баклея – Леверетта является зависимость скорости распространения насыщенности от её величины. Это явление называется дисперсией волн. При 0 £ s £sп большие насыщенности распространяются с большими скоростями, а при sп< s £1 скорость распространения постоянного значения насыщенности начинает уменьшаться. Последнее приводит к тому, что, начиная с некоторого момента времени, распределение насыщенности оказывается многозначным (рис.5.10, кривая 1–2–3–4–5). В области данного участка одному и тому же значению х соответствуют три значения насыщенности s: s1, s2 и s3, что физически невозможно, так как в каждом сечении пласта в любой момент времени может существовать только одна насыщенность. Данная неоднозначность устраняется введением скачка насыщенности (рис.5.11, отрезок 1–3–5). Скорость распространения скачка при этом равна скорости распространения насыщенности. Необходимо отметить, что в действительности математический скачок насыщенности не имеет места. Он появляется в решении вследствие пренебрежения капиллярными силами, за счет которых появляется некоторая “переходная зона” вблизи фронта вытеснения, в которой насыщенность изменяется непрерывно.
В общем случае неодномерного вытеснения, а также при учете сжимаемости одной из фаз рассмотренная задача уже не сводится к одному уравнению для насыщенности. Необходимо совместно определять давление и насыщенность. Численные решения таких задач могут быть получены лишь на ЭВМ.
Задача Рапопорта – Лиса
Учет капиллярного скачка давления рк, который задается в виде известной эмпирической функции насыщенностей, приводит к теории следующего приближения–модели Рапопорта – Лиса. При этом пренебрегаем силой тяжести.
Действие капиллярных сил проявляется в основном вблизи фронта вытеснения, где градиенты насыщенности велики. Эти силы приводят к “размазыванию” фронта, поэтому при учете капиллярных сил скачок насыщенности отсутствует и насыщенность изменяется непрерывно.
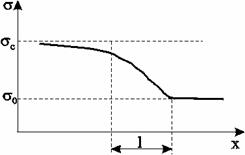
Рис. 5.11. Распределение насыщенности в стабилизированной зоне
Тем не менее, экспериментально было обнаружено существование так называемой стабилизированной зоны насыщенности, которая перемещается, не изменяя своей формы, и распределение насыщенности в ней при постоянной скорости вытеснения – стационарно. В теории Баклея – Лаверетта (при пренебрежении капиллярными силами) стабилизированная зона моделируется скачком. Модель Рапопорта – Лиса позволяет определить ширину данной зоны l(рис. 5.11) и распределение насыщенностей по ней.
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
1. Гомо- и гетерогенные системы.
2. Насыщенность порового пространства i –й фазой.
3. Скорость фильтрации i –й фазы.
4. Закон Дарси для i –й фазы.
5. Зависимость относительных проницаемостей от насыщенности.
6. От каких параметров зависит относительная проницаемость?
7. Что такое капиллярное давление и от каких параметров оно зависит?
8. Почему сумма относительных проницаемостей меньше 1?
9. Нарисуйте диаграмму для определения границ преобладания потоков различных фаз при трехфазном течении.
10. Как зависит функция Леверетта от насыщенности в случае насыщения и пропитки?
11. Уравнения неразрывности для двухфазного потока в случае сжимаемых и несжимаемых сред.
12. От каких параметров зависит капиллярное давление?
13. Что такое недонасыщенная нефть?
14. Условия существования газированной нефти.
15. Общее дифференциальное уравнение одномернного потока капельно-жидкой фазы, растворенного и свободного газа газированной жидкости.
16. Массовая растворимость газа в жидкости.
17. Объемный газовый фактор.
18. Объемная растворимость газа в жидкости.
19. Закон Генри растворимости газа в жидкости.
20. Чему равно значение равномерной насыщенности?
21. Объемный коэффициент нефти.
22. Как зависит растворимость от давления?
23. Определить дебит газированной жидкости по формулам гомогенной.
24. Отличие формулы для определения дебита газированной жидкости от формулы Дюпюи по физическому содержанию.
25. Взаимосвзь дебитов газированной и гомогенной жидкостей.
26. Зависимость дебита газированной жидкости от величины пластового давления. Физическое объяснение.
27. Отличие идикаторной диаграммы газированной жидкости от гомогенной.
28. Особенности поведения дебитов и газового фактора для газированной жидкости во время пуска скважины.
29. Классы пород по степени смачиваемости.
30. Допущения теории одномерного движения двухфазной жидкости в пористой среде.
31. Функция Баклея – Леверетта или функция распределения потоков фаз.
32. Граничные условия для уравнения изменения насыщенности.
33. Сущность концевого эффекта.
34. Модель Рапопорта – Лиса.
35. Модель Баклея – Леверетта.
36. Вид функции Баклея –Леверетта и её производной.
37. Физический смысл функции Баклея –Леверетта.
38. Характер изменения функции Баклея –Леверетта в зависмости от изменения относительной вязкости.
39. Дисперсия волн.
40. Физическая природа скачка насыщенности.
41.Стабилизированная зона насыщенности.
