Глава 3. установившаяся потенциальная одномерная фильтрация

При данных условиях ¶ / ¶ t=0 и Dj=0. (3.1)

Виды одномерных потоков

Одномерным называется поток, в котором параметры являются функцией только одной пространственной координаты, направленной по линии тока. К одномерным потокам относятся:

1) прямолинейно-параллельный:

2) плоскорадиальный;

радиально-сферический.

Прямолинейно-параллельный поток

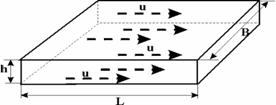
Рис. 3.1. Схема прямолинейно-параллельного течения

Траектории всех частиц жидкости – параллельные прямые, а скорости фильтрации во всех точках любого поперечного (перпендикулярного к линиям тока) сечения потока равны между собой, поверхности равных потенциалов (эквипотенциальные поверхности) и поверхности равных скоростей (изотахи) являются плоскими поверхностями, перпендикулярными траекториям. Законы движения вдоль всех траекторий такого фильтрационного потока идентичны, а потому достаточно изучить движение вдоль одной из траекторий, которую можно принять за ось координат – осьх.

Примеры

а) Пласт (рис.3.1) имеет в плане полосообразную форму шириной B и длиной L, толщина пласта h постоянна, граничный контур непроницаем и непроницаемы кровля и подошва пласта. Батарея эксплуатационных скважин расположена параллельно начальному контуру нефтеносности. Приближение тем лучше, чем меньше расстояние между скважинами и если заменить батарею сплошной прямолинейной выработкой – галереей, то движение жидкости к галерее будет строго прямолинейно–параллельным.

б) Поток между круговыми батареями нагнетательных и эксплуатационных скважин в случае больших радиусов батарей (угол схождения векторов скорости бесконечно мал). При этом толщина пласта постоянна, а его кровля и подошва непроницаемы.

в) В лабораторных условиях при течении через цилиндрический керн или прямую трубу постоянного сечения, заполненную пористой или трещинной средой.

Плоскорадиальный поток

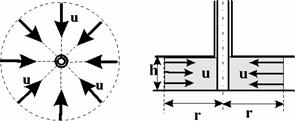
a b

Рис. 3.2. Схема плоскорадиального течения: a – горизонтальное сечение; b –вертикальное сечение

Траектории всех частиц жидкости – прямолинейные горизонтальные прямые, радиально сходящиеся к центру скважины, а скорости фильтрации во всех точках любого поперечного (перпендикулярного к линиям тока) сечения потока параллельны и равны между собой; изотахи и эквипотенциальные поверхности перпендикулярны траекториям и образуют цилиндрические окружности с осью, совпадающей с осью скважины. Схемы линий тока в любой горизонтальной плоскости потока будут идентичными и для характеристики потока достаточно рассмотреть движение жидкости в одной горизонтальной плоскости.

Примеры

а) Горизонтальный пласт постоянной толщины h и неограниченной протяженности, подошва и кровля пласта непроницаемы. Пласт вскрыт единственной гидродинамически совершенной скважиной (рис.3.2), то есть. вскрыт на всю толщину, и забой полностью открыт. Для эксплуатационной скважины поток – радиально-сходящийся, а для нагнетательной – радиально-расходящийся. Плоскорадиальным потоком будет занята вся зона от стенки скважины до контура питания.

б) Гидродинамически несовершенная скважина (скважина с перфорированным забоем – несовершенство по характеру вскрытия или не полностью вскрывшая пласт – несовершенство по степени вскрытия). Вблизи скважины линии тока искривляются, и поток можно считать плоскорадиальным только при некотором удалении от скважины.

в) Круговая батарея эксплуатационных скважин – поток плоскорадиален на некотором удалении, т.к. жидкость движется как бы к укрупнённой скважине радиуса, равного радиусу окружности батареи.

Радиально-сферический поток

Траектории всех частиц жидкости – прямолинейные горизонтальные прямые, радиально сходящиеся к центру полусферического забоя; эквипотенциальные поверхности перпендикулярны траекториям и образуют сферические поверхности. Скорость фильтрации в любой точке потока является функцией только расстояния этой точки от центра забоя. Следовательно, этот вид фильтрационного потока также является одномерным.

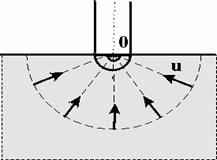
Рис. 3.3. Схема радиально-сферического течения

Такой поток может реализовываться, когда скважина вскрывает только плоскую горизонтальную, непроницаемую кровлю пласта (рис.3.3). Пласт при этом должен быть неограниченной толщины, а забой иметь полусферическую форму. Приближение к данному виду потока тем лучше, чем глубина вскрытия меньше толщины пласта.

Описанные три вида одномерного потока играют большую роль при решении многих задач нефтегазопромысловой практики. Естественно, моделируя реальное течение одним из трёх указанных видов, мы прибегаем к некоторой схематизации реальных пластов и течений жидкости. Тем не менее, рассмотренные схемы не только воспроизводят, хотя и приближенно простейшие случаи течения жидкости в реальном пласте, но и помогают изучать более сложные виды потоков пластовой жидкости в тех случаях, в которых сложный фильтрационный поток удобно представить себе состоящим из простейших видов потока.