Уравнения фильтрации для трещинно-пористой среды

В чисто трещинном пласте система уравнений имеет тот же вид, что и в пористом. Для трещинно-пористой среды следует учитывать её характерные особенности:

1) моделирование связано с порами разных масштабов (среда 1 – роль поровых каналов играют трещины, а роль зёрен – пористые блоки; среда 2 – обычная пористая среда, образующая блоки);

2) между отмеченными средами при фильтрации возникает переток жидкости из пористых блоков в трещины в пределах выделенного элементарного объёма трещинно-пористого пласта.

При этом предполагается, что в каждом элементарном объёме трещинно-пористого пласта содержится большое число пористых блоков, так что в окрестности каждой точки вводится две скорости фильтрации, два давления, относящиеся к средам 1 и 2. На основании сказанного, уравнения неразрывности выписываются для каждой из сред, а переток учитывается членом q_1,2. Наличие перетока эквивалентно существованию внутренних источников жидкости в выделенном объёме.

Для жидкости, находящейся в трещинах, имеем:

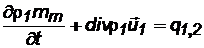. (2.33)

Для жидкости в пористых блоках

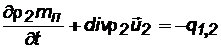. (2.34)

Здесь q_1,2 – масса жидкости, поступающей из пористых блоков в трещины за единицу времени на единицу объёма (размерность МL^-3T^-1, где М – размерность массы, L – расстояния и Т – времени).

Будем полагать, что q_1,2 пропорционально разности фильтрационных потенциалов первой и второй сред

q_1,2=Q (j₂ - j₁),(2.35)

где Q– коэффициент переноса, размерности L^-2.

Для чисто трещинного пласта считаем q_1,2=0 и тогда будем иметь только одно уравнение неразрывности для жидкости в системе трещин (в пористых блоках не содержится жидкость). При установившейся фильтрации жидкости в трещинно-пористом пласте, когда во всём пласте существует только одно давление р₁=р₂=р, получаем

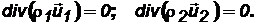(2.36)

Для чисто трещинного пласта

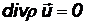. (2.37)

Начальные и граничные условия

Выше было показано, что уравнения фильтрации сводятся к одному уравнению второго порядка относительно потенциала. В связи с этим, рассмотрим начальные и граничные условия для данного уравнения.

Начальные условия

j = j_о(x,y,z) при t = 0,(2.38)

если при t = 0 пласт не возмущён, тоj = j_о = const.

Граничные условия

Число граничных условий равно порядку дифференциального уравнения по координатам. Граничные условия задаются на границах пласта (внешние) и на забое скважины (внутренние).

А) Внешняя граница Г

1)постоянный потенциал

j(Г,t)=j_к=const, (2.39)

т.е. граница является контуром питания;

2) постоянный переток массы через границу

G = Fr`u = const, т.е. используя уравнение (2.30),

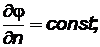(2.40)

3) переменный поток массы через границу

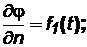(2.41)

4) замкнутая внешняя граница

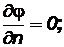(2.42)

5) бесконечный пласт

lim_x®¥ j(Г,t) = j_к = const.(2.43)

у®¥

В) Внутренняя граница

1) постоянный потенциал на забое скважины, радиуса r_c

j(r_c , t)=j_c=const ; (2.44)

2) постоянный массовый дебит (при условии выполнения закона Дарс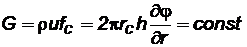и) или

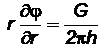при r=r_c; (2.45)

3) переменный потенциал на забое

j(r_c ,t)=f₂(t) при r=r_c;(2.46)

4) переменный массовый дебит

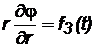при r=r_c; (2.47)

5) неработающая скважина

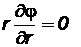при r=r_c. (2.48)

Замыкающие соотношения

Для полного замыкания системы уравнений фильтрационного течения необходимо знание зависимостей r,m,k,μ от давления.