Теорема умножения вероятностей зависимых событий

Вероятность совместного появления двух зависимых событий А и В равна произведению вероятности одного из них на условную вероятность P_А(B) другого, вычисленную в предположении, что первое событие уже наступило, то есть:

P(AB) = P(A) ^.P_А(B).

В этой формуле условная вероятность P_A(B) выражает вероят­ность появления события B при условии, что событие A уже наступи­ло.

Формула полной вероятности. Вероятности гипотез

Возможны случаи, когда появление события А зависит от нескольких событий. В этом случае, вероятность события А, которое может наступить лишь при условии появления одного из несовместных событий B₁, B₂, ... B_n, образующих полную группу, равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероятность события А:

Р(А) = Р(В₁) 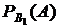+ Р(В₂) 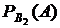+ ... + Р(В_п) .

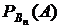Эту формулу называют формулой полной вероятности, а события B₁, B₂, ..., B_n −гипотезами, поскольку заранее не известно, какое из этих событий наступит.

Формулы Бейеса

Формулы Бейеса позволяют переоценить вероятности гипотез после того, как становится известным результат испытания, в ре­зультате которого появилось событие А.

Пусть событие А может наступить лишь при условии появления одного из несовместных событий (гипотез) В₁, В₂, ..., В_n, образующих полную группу. Вероятность появления события А определяется по формуле полной вероятности, которая была рассмотрена выше.

Допустим, что произведено испытание, в результате которого появилось событие А. Требуется определить, как изменились вероятности гипотез, то есть найти условные вероятности Р_А(В₁), Р_А(В₂), ..., Р_А(В_n).

В общем случае условная вероятность любой гипотезы В_i может быть вычислена по следующей формуле:

.

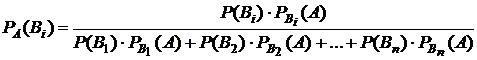Повторение испытаний

В этой теме рассматриваются вопросы, связанные с испытаниями, которые повторяются несколько раз. В результате каждого испытания интересующее нас событие может появиться или не появиться_.

Условимся считать, что вероятность появления события в каждом испытании постоянна и равна p. Следовательно, вероятность не появления события в каждом испытании также постоянна и равна 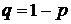(как вероятность противоположного события).

Ставится задача: найти вероятность того, что в n испытаниях событие A осуществится ровно kраз и, следовательно, не осуществится n-k раз. Эту вероятность обозначают P_n(k) и вычисляют по формуле Бернулли:

.

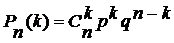Локальная теорема Лапласа

Формулу Бернулли удобно применять при небольших значениях n. Применять указанную формулу при значениях n > 30 трудно, так как эта формула потребует выполнения действий над громадными числами. Существует формула, которая позволяет приближенно найти вероятность появления события ровно k раз в n испытаниях, если число испытаний достаточно велико, ее называют локальной теоремой Лапласа.

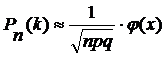
где .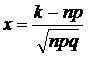

Значения функции 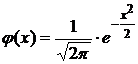приведены в Приложении 1, где указаны значения функции при положительных значениях аргумента x. Для отрицательных значений x пользуются теми же таблицами, так как функция j(х) четная, то есть j(–х) = j(х).