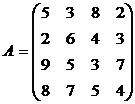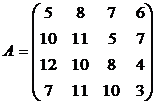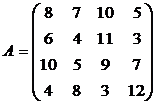Антагонистические матричные игры с нулевой суммой имеющие решение в смешанных стратегиях.

К сожалению, решение игры в чистых стратегиях удается найти не так часто, как нам этого хотелось бы (это ведь совсем несложно сделать, и читатель уже в этом убедился). В таких случаях чистые стратегии уступают место смешанным.

Определение. Смешанной стратегией игрока A в игре Г называется вероятность распределения вектора 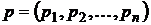на множестве чистых стратегий .

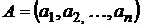Вероятность 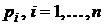означает, что первый игрок выбирает свою i-ю стратегию с данной вероятностью. Вектор 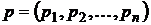удовлетворяет нормировочному условию теории вероятностей .

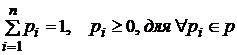Определение. Смешанной стратегией игрока B в игре Г называется вероятность распределения вектора 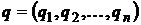на множестве чистых стратегий .

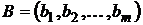Вероятность 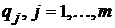означает, что первый игрок выбирает свою j-ю стратегию с данной вероятностью. Вектор 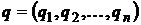удовлетворяет нормировочному условию теории вероятностей .

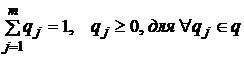Теорема (основная теорема матричных игр). Всякая матричная игра имеет решение в смешанных стратегиях.

Обозначим через 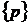- множество всех смешанных стратегий первого игрока на множестве A. Мы уже упоминали, что решение игры в смешанных стратегиях существует только тогда, когда не существует решение в чистых стратегиях. Поэтому все вектора p, такие, что один элемент равен 1, а остальные нулю, из множества 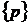мы исключим, так как они равносильны применением игроком чистой стратегии. Аналогично, через 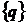обозначим множество смешанных стратегий второго игрока на множестве B и так же исключим все единичные вектора.

Построим смешанное расширение антагонистической игры.

Определение. Антагонистическая игра

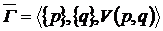
называется смешанным расширением игры Г.

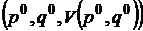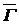Определение. Решение игры называется решением исходной игры Г в смешанных стратегиях. При этом вектор 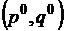называется вектором оптимальных смешанных стратегий игроков, а 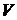- выигрышем или значением игры и выполняются условия:

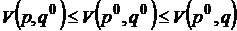, для .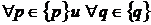

Значение игры является математическим ожиданием выигрыша при применении игроками своих оптимальных стратегий 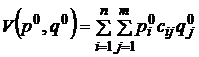. Это значение легко найти, если известны оптимальные значения векторов распределения вероятностей. Но оптимальные вектора тоже необходимо найти. Рассмотрим различные методы решения матричных игр в смешанных стратегиях.

Решение игр

Решение игры 2х2

Самой простой игрой является игра, в которой каждый из двух игроков имеет по две стратегии. Тогда платежная матрица игры будет иметь две строки и два столбца.

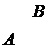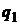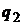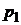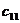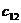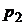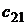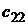Воспользуемся определением решения игры. Рассмотрим игру сначала с позиции первого игрока. Пусть второй игрок применил свою оптимальную стратегию, а первый – любую, кроме оптимальной. Уже упоминалось, что чистая стратегия не может быть оптимальной, поэтому стратеги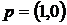и и 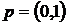нам подходят (они априори не могут быть оптимальными). Воспользуемся левой частью двойного неравенства и математическим ожиданием выигрыша, не забудем и про нормировочное условие. Тогда получим систему из двух неравенств и одного уравнения

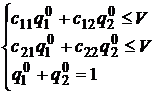, где ,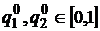

То есть умножим вектор 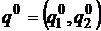сначала на первую строку матрицы, а затем на вторую. Первые два неравенства системы всегда будут выполняться как верные равенства. Тогда система примет вид:

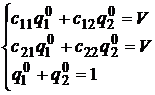
Вычтем второе уравнение из первого, приведем подобные и получим систему из двух уравнений с двумя переменными:

.

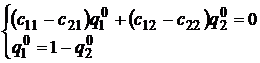Подставляя в первое уравнение выраженное значение для 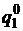, получим уравнение: 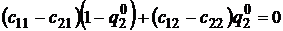, приводя подобные, найдем выражение для нахождения :

,

.

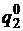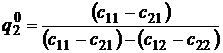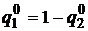Таким образом, оптимальный вектор распределения вероятностей найден и осталось только найти выигрыш. Для этого необходимо подставить значения вероятностей в первое или второе уравнения системы. Таким образом, решив данную систему, найден вектор оптимального распределения вероятностей второго игрока и выигрыш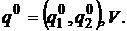

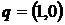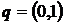Теперь рассмотрим правую часть двойного неравенства. Первый игрок применяет свою оптимальную стратегию, а второй любую, кроме оптимальной, например чистые и . Воспользуемся правой частью двойного неравенства и математическим ожиданием выигрыша, не забудем и про нормировочное условие. Тогда получим систему из двух неравенств и одного уравнения

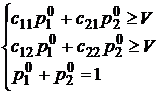, где ,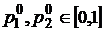

на этот раз умножаем вектор 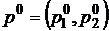на столбцы матрицы. Первые два неравенства системы всегда будут выполняться как верные равенства. Тогда система примет вид:

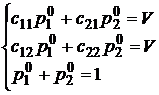
Вычтем второе уравнение из первого, приведем подобные и получим систему из двух уравнений с двумя переменными:

,

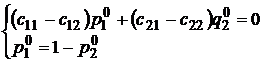Подставляя в первое уравнение выраженное значение для 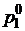получим уравнение: 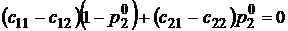, приводя подобные, найдем выражение для нахождения :

,

.

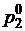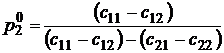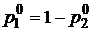Таким образом, оптимальный вектор распределения вероятностей первого игрока найден и осталось только найти выигрыш. Для этого надо подставить значения вероятностей в первое или второе уравнение системы. Таким образом, решив данную систему найден вектор оптимального распределения вероятностей второго игрока и выигрыш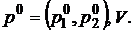

Так как в условии в общем виде решения игры, когда оба игрока применяют свои оптимальные стратегии, одинаково, то и выигрыш при решении обоих систем должен быть одинаковым. Это условие и будет проверкой правильности решения задачи.

Пример. Найти решение игры 2х2

.

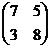Решение. Эта игра не имеет решение в чистых стратегиях, так как 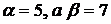. Значит, в соответствии с основной теоремой матричных игр, она должна иметь решение в смешанных стратегиях. Рассуждения аналогичны решению задачи в общем виде, поэтому они приводиться еще раз не будут, запишем сразу системы:

.

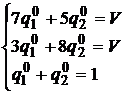
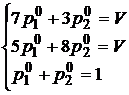Вычтем из первых строк вторые и приведем подобные:

.

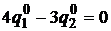
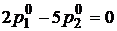
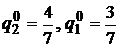
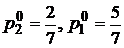
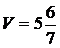
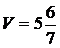Выигрыши в обоих случаях совпали, значит задача решена правильно.

Ответ: .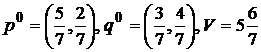

Задачи для самостоятельного решения.

Решить игру 2х2:

1. 2. 3. 4.

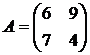
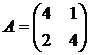
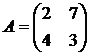
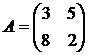
5. 6. 7. 8.

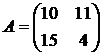
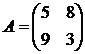
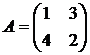
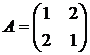
9. 10. 11. 12.

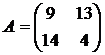
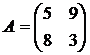
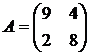
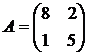
13. 14. 15. 16.

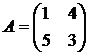
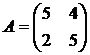
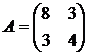
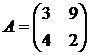
17. 18. 19. 20.

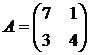
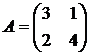
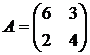
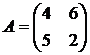
Принцип доминирования

Матрицы размерностью 2х2 встречаются не так часто, как нам того бы хотелось, поэтому рассмотрим принцип, позволяющий уменьшить размерность матрицы.

Первый игрок стремиться максимизировать свой выигрыш и ему будет выгодна та стратегия, которая принесет больший выигрыш. Если элементы некоторой строки платежной матрицы С меньше соответствующих элементов другой строки, то интуитивно ясно, первую можно вычеркнуть. Сформулируем условия доминирования строк и столбцов платежной матрицы, позволяющие уменьшить ее размерность.

Определение. Вектор 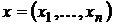доминирует вектор 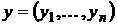, если все элементы вектора x больше или равны соответствующим элементам вектора y. То есть 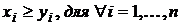, и хотя бы одно неравенство выполняется как строгое. Про вектор y говорят, что он доминируется вектором x.

Определение. Линейная комбинация векторов называется выпуклой, если существуют такие коэффициенты 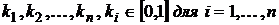, не равные нулю одновременно, что выполнено условие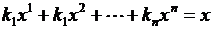

Теорема (о доминировании строк). Если в игре с платежной матрицей С какая-либо строка доминируется выпуклой комбинацией остальных строк, то она будет входить с нулевой вероятностью в оптимальную смешанную стратегию первого игрока и ее можно вычеркнуть.

Замечания к теореме:

1. Если в матрице существуют несколько одинаковых срок, то все, кроме одной можно вычеркнуть, и они будут входить с нулевой вероятностью в оптимальную смешанную стратегию первого игрока.

2. Если какая-либо строка доминируется другой, то меньшую можно вычеркнуть.

Теорема (о доминировании столбцов). Если в игре с платежной матрицей C какой-либо столбец доминирует выпуклую комбинацию остальных столбцов, то он будет входить с нулевой вероятностью в оптимальную смешанную стратегию второго игрока и его можно вычеркнуть.

ПримерИспользуя принцип доминирования найти оптимальную стратегию.

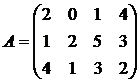
Решение. Третий и четвертый столбец доминируют над вторым, поэтому, в соответствии с утверждением о доминировании строк, их можно вычеркнуть и они будут входить с нулевой вероятностью в оптимальную смешанную стратегию второго игрока.

Из оставшихся трех строк и двух столбцов, можно вычеркнуть первую строку, так как она доминируется третьей строкой. Оставшуюся игру 2х2 просто решить. Таким образом, оптимальными смешанными стратегиями игроков будут: , , .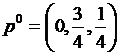

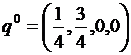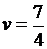Задачи для самостоятельного решения.

Используя принцип доминировании, решить игру:

1. 2. 3.

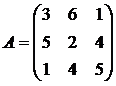
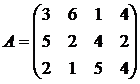
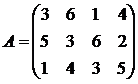
4. 5. 6.

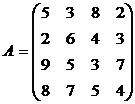
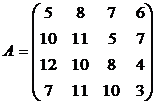
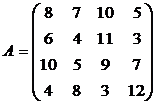
7. 8. 9.

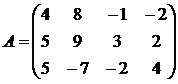
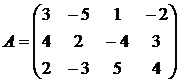
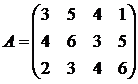
10. 11. 12.