Модель, ПГР, стационарное решение и распределение времени ожидания в системах с ограниченной очередью
- Модель.
Исходные данные те же самые
Входящий поток – простейший с параметром 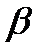
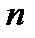 - количество линий,
- количество линий, 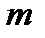 - максимально допустимый размер очереди
- максимально допустимый размер очереди
Если в момент поступления вызова существует свободная линия – вызов приступает к разговору, если все линии заняты, то
· вызов остается в СО, если длина очереди 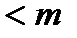
· вызов получает отказ, если длина очереди 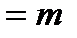
Пример – система с ограниченным числом мест ожидания (зал ожидания)
СОЧ относится к классу смешанных СО (есть и время обслуживания, и время ожидания)
Состояние СО 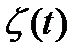
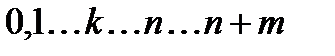
Всего (n+m+1) состояний
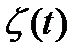 =k означает:
=k означает:
-
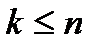 - k линий заняты (k вызовов на обслуживании), значит (n-k) свободны
- k линий заняты (k вызовов на обслуживании), значит (n-k) свободны -
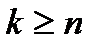 - заняты все n линий (n вызовов на обслуживании) и имеется очередь=(k-n)
- заняты все n линий (n вызовов на обслуживании) и имеется очередь=(k-n)
- ПГР
Утверждение: в случае СОЧ случайный процесс 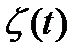 является Марковским ПГР с параметрами
является Марковским ПГР с параметрами 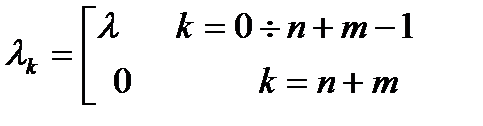 ;
; 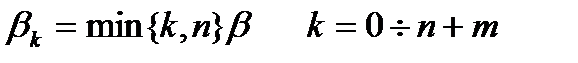
Док-во: То же, что и для СОЖ
-
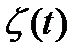 – Марковский по теореме (входящий поток простейший, а время обслуживания распределено по показательному закону)
– Марковский по теореме (входящий поток простейший, а время обслуживания распределено по показательному закону) -
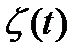 – ПГР
– ПГР -
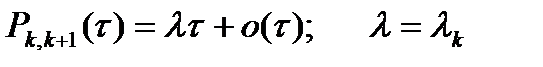
-
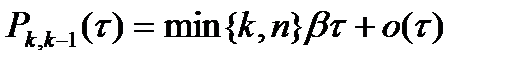
-
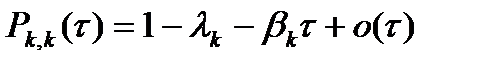
- Стационарное решение
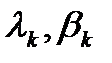 - те же, что и для СОЖ, значит
- те же, что и для СОЖ, значит 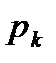 через
через 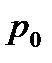 .
. 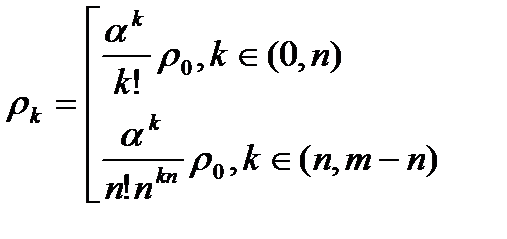 (**)
(**)
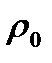 - другое
- другое 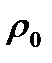 - ?
- ?
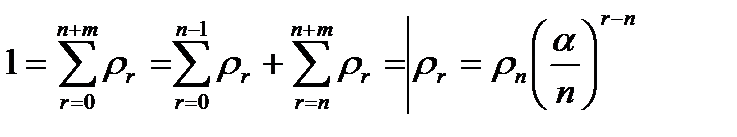 конечен.
конечен. 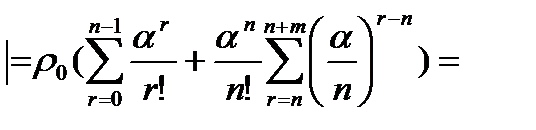 |
| 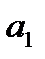 -первый член прогрессии, q – знам-ль,
-первый член прогрессии, q – знам-ль, 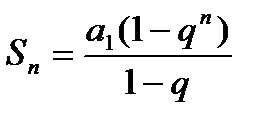 .
. 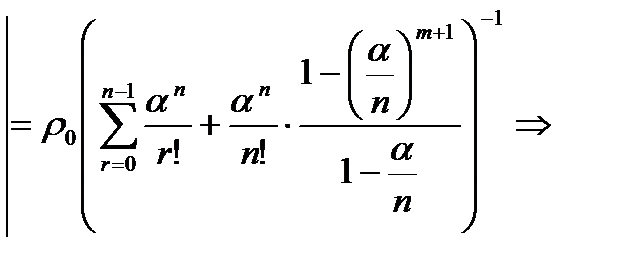 подставляя
подставляя  в (**), получаем
в (**), получаем  (m+1 – число слагаемых).
(m+1 – число слагаемых).
- Распределение времени ожидания
Сохраняем обозначения и рассужд в случае сож. => получаем
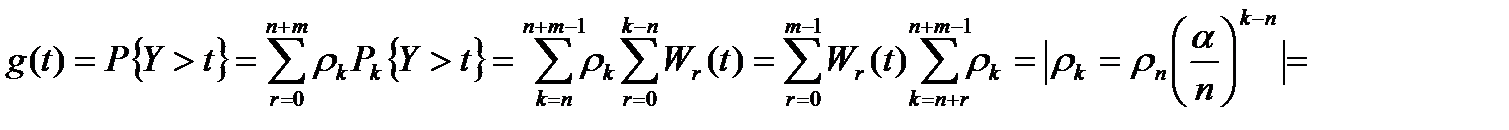
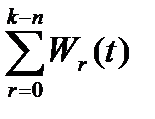 - длина очереди освобождений линий
- длина очереди освобождений линий
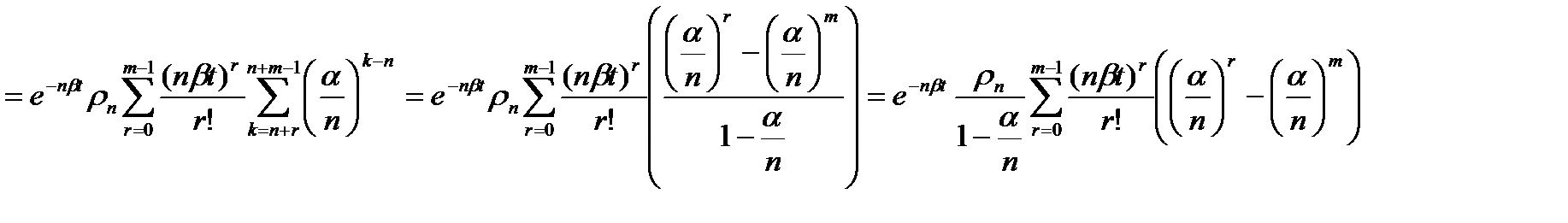 поток освобождений (простейший)
поток освобождений (простейший) 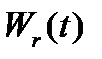 =
= 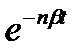 (
( 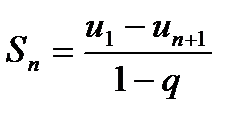 – сумма геометрической прогрессии).
– сумма геометрической прогрессии).
Показатели эффективности СОЧ
- Вероятность отказа
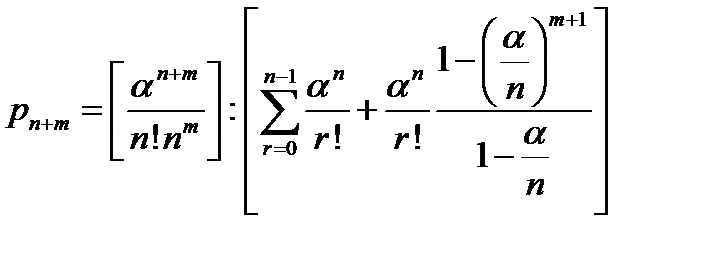
Вероятность того, что вызов будет обслужен 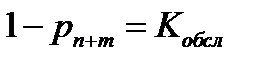 - коэффициент обслуживания (средняя доля обслуженных)
- коэффициент обслуживания (средняя доля обслуженных)
2 исхода 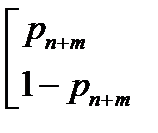
Потоки отказов обслуженных вызовов являются простейшими с параметрами λ 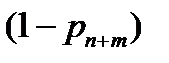 и λ
и λ 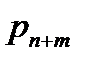 соответственно (из свойства раси..) простейшие потоки).
соответственно (из свойства раси..) простейшие потоки).
Замечание: m=0: 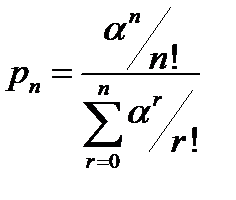 ;
; 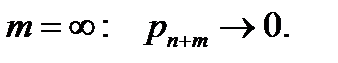
2. Среднее число занятых линий - число занятых линий
Состояния СО: 0, 1, …, n-1, n, n+1, …, n+m
 : 0, 1, …, n-1, n
: 0, 1, …, n-1, n
Вероятности: 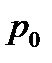 ,
, 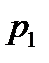 , …,
, …, 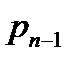 ,
, 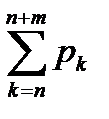
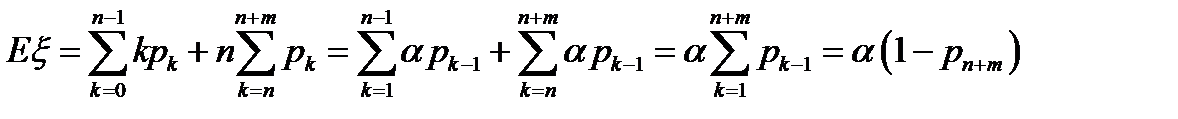
При m=0 - СОТ => 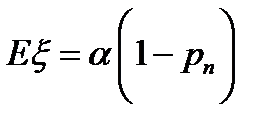
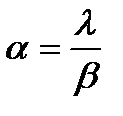
Замечание. 
Интерпретация E 
А) 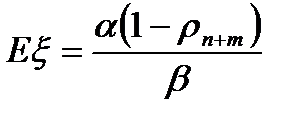 = [интенсивность обслуженных вызовов]:[интенсивность обслуживания на любой линии]
= [интенсивность обслуженных вызовов]:[интенсивность обслуживания на любой линии]
Б) 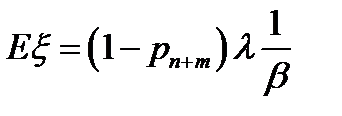 =[ср число обслуженных за единицу времени]*
=[ср число обслуженных за единицу времени]* 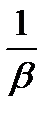 =:[среднее число обслуженных вызовов за
=:[среднее число обслуженных вызовов за 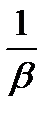 ]
]
Способ 1: (используя стационарное решение - 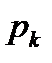 )
)
Состояния СО: 0, 1, …, n-1, n, n+1, …, n+m
Y: ((0, 1, …, n-1) – 0; (n, n+1, …, n+m-1) >0; n+m – 0)
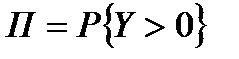 =
= 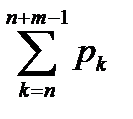 =
= 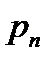
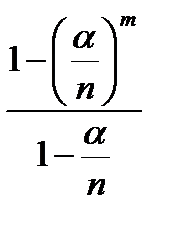
Способ 2: (используя функцию распределения)
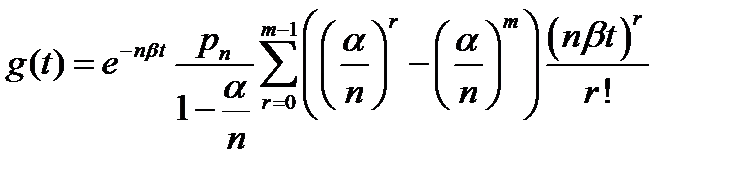
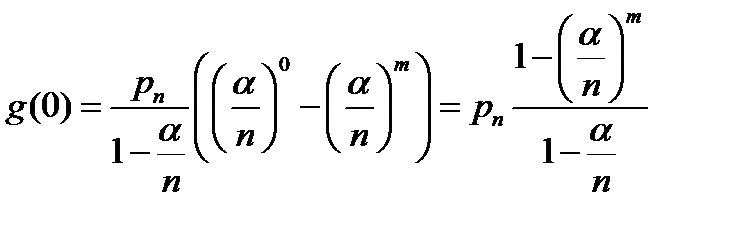
Замечания:
А) m=0 - СОТ: 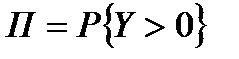 =0 ~
=0 ~ 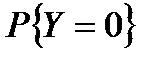 =1
=1
Б) m=  П=
П= 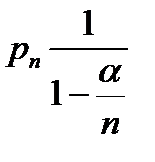 для СОЖ.
для СОЖ.
- Вероятность полной загрузки. (Вероятность того, что все линии заняты).
Пусть (полная загрузкаà) π=П+ 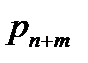 =
= 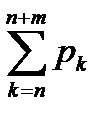 =(геометрическая прогрессия)=
=(геометрическая прогрессия)=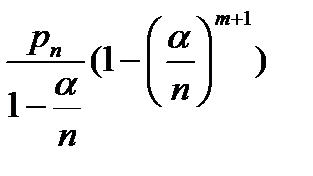
Смежный показатель – вероятность того, что есть свободная линия (вероятность немедленного обслуживания).
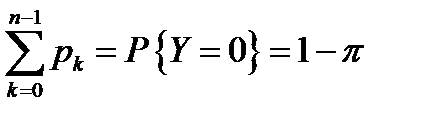
- Среднее время ожидания обслуживания.
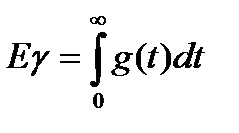 =
= 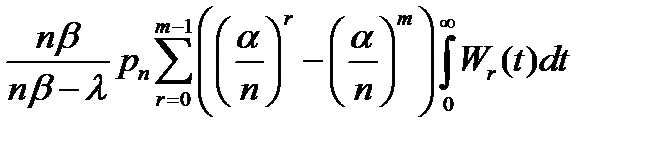 = (
= ( 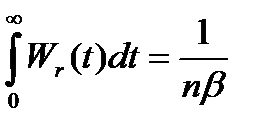 ) в соответствии с площадью под кривой Пуассона) =
) в соответствии с площадью под кривой Пуассона) = 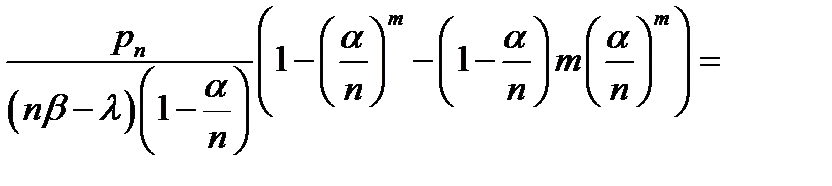
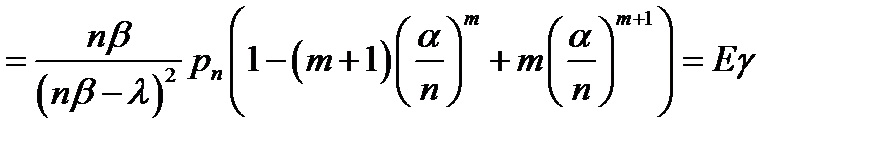
6. Среднее время пребывания вызова в СО
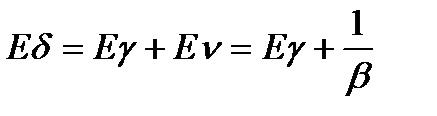
7. Средняя длина очереди:
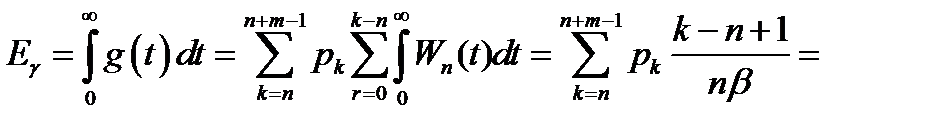
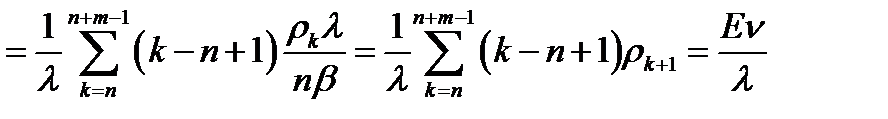
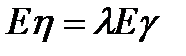
8. Среднее число вызовов в СО
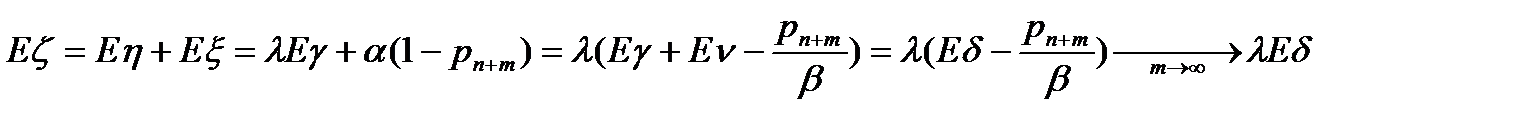
25.Оптимальное число линий в СОЧ (на примере расчета оптимального размера максимального запаса товара при задалживании спроса)
СО – магазин
Входящий поток – поток покупателей
Допущения и исходные данные:
1. Поток покупателей – простейший с параметром 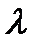 :
:
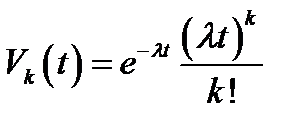 ;
; 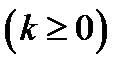 ;
; 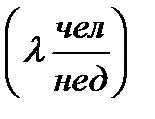
2. В одни руки отпускается только одна единица товара (спрос –пуассоновский) 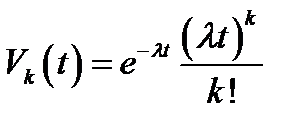
3. Как только происходит продажа товара, сразу же происходит заказ на ее замену другой единицей. Следовательно, число, равное сумме размера запаса товара и количества поданных заявок, является константой на любой момент времени
4. 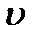 - время выполнения заказов на пополнения запаса. Распределено по показательному закону -
- время выполнения заказов на пополнения запаса. Распределено по показательному закону - 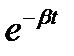
5. При отсутствии товара в магазине он задалживается, но не более чем для m покупателей
6. Пусть 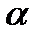 - доход от продажи единицы товара за вычетом издержек выполнения заказа на его доставку
- доход от продажи единицы товара за вычетом издержек выполнения заказа на его доставку
7. 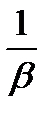 - среднее время выполнения заказов
- среднее время выполнения заказов
Пусть 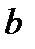 - издержки хранения единицы товара за единицу времени. Пусть
- издержки хранения единицы товара за единицу времени. Пусть 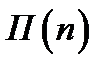 - средняя прибыль магазина за
- средняя прибыль магазина за 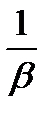 .
. 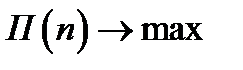 .
. 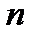 - либо максимальный размер запаса товара в магазине, либо максимальное число поданных заявок.
- либо максимальный размер запаса товара в магазине, либо максимальное число поданных заявок.
Для решения можно воспользоваться моделью СОЧ
Линия – ячейка. 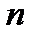 - количество линий
- количество линий
Линия занята/свободна – ячейка пуста/заполнена. Обслуживание – выполнение заказа на заполнение пустой ячейки. Время обслуживания распределено показательно 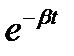
Состояние СО - 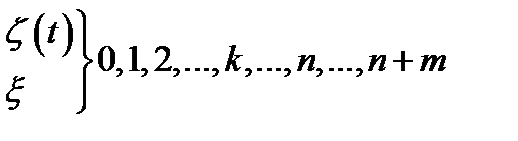 - количество поданных заказов. Если
- количество поданных заказов. Если 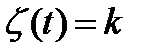 , то:
, то:
a. при 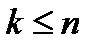 - подано “
- подано “ 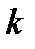 ” заявок. Следовательно, размер запаса товара равен
” заявок. Следовательно, размер запаса товара равен 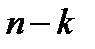
b. при 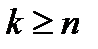 - подано “
- подано “ 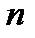 ” заявок и имеется очередь из
” заявок и имеется очередь из 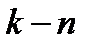 покупателей
покупателей
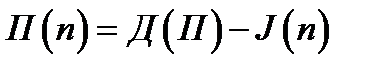 , где
, где 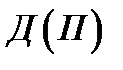 - доходы;
- доходы; 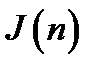 - издержки.
- издержки.
Доходы приносят реализованные единицы товара. Среднее число реализованных единиц товара за 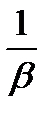 -
- 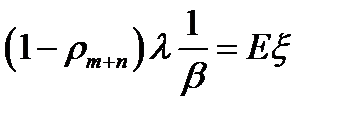 .
.
Издержки 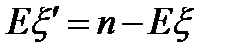 . Тогда
. Тогда 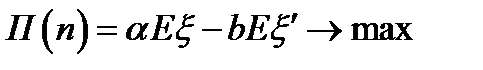
Модель замкнутой СО
I. Исходные данные
] n – количество станков в группе станков. Станки выполняют одинаковые операции. m – количество обслуживаемых объектов. ] n<m<∞ (n≥m – неинтересный случай, так как часть станков постоянно простаивает).
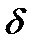 - время исправной работы объекта.
- время исправной работы объекта.
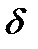 - непрерывная случайная величина, распределенная по показательному закону с параметром
- непрерывная случайная величина, распределенная по показательному закону с параметром 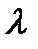 .
. 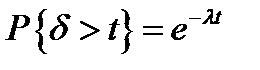 . В течение исправной работы объект находится вне СО.
. В течение исправной работы объект находится вне СО.
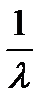 - среднее время исправной работы объекта (нахождения его вне СО). В момент поломки объект попадает в СО. Если в этот момент существует свободная линия, объект занимает ее. Если все линии оказывается, заняты – объект становится в очередь и находится в ней в течение времени
- среднее время исправной работы объекта (нахождения его вне СО). В момент поломки объект попадает в СО. Если в этот момент существует свободная линия, объект занимает ее. Если все линии оказывается, заняты – объект становится в очередь и находится в ней в течение времени 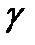 .
. 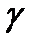 – неотрицательная непрерывная случайная величина.
– неотрицательная непрерывная случайная величина.
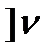 - время обслуживания объекта (его ремонта).
- время обслуживания объекта (его ремонта).
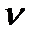 - положительная непрерывная случайная величина, распределенная по показательному закону с параметром
- положительная непрерывная случайная величина, распределенная по показательному закону с параметром 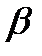 . По окончании ремонта объект покидает СО, и в дальнейшем снова становится источником поступления вызова.
. По окончании ремонта объект покидает СО, и в дальнейшем снова становится источником поступления вызова.
II. Названия СО.
Замкнутые СО: в рассматриваемой ситуации входящий поток вызовов формируется из выходящего.
| Входящий поток – поток сломанных объектов |
| Объект вне СО |
| Поток отремонтированных объектов |
| Выходящий поток |
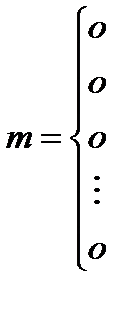
Циклические СО: для  объекта существует следующий цикл:
объекта существует следующий цикл:

 объекта
объекта 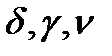
СОЖ: отказов нет, однако входной поток ограничен 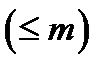 ( “m” объектов в СО значит, что все объекты сломаны)
( “m” объектов в СО значит, что все объекты сломаны)
III. Состояния СО.
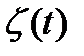 :0, 1, 2, … , k, …n, …m. – m+1 состояние
:0, 1, 2, … , k, …n, …m. – m+1 состояние
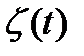 =k означает:
=k означает:
а) 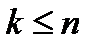 - в СО находятся ровно k сломанных объектов (занято k линий пучка).
- в СО находятся ровно k сломанных объектов (занято k линий пучка).
б) 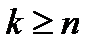 - заняты все n линий и k-n объектов стоят в очереди.
- заняты все n линий и k-n объектов стоят в очереди.
Если 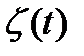 =k <=> m-k объектов исправны и находятся вне СО.
=k <=> m-k объектов исправны и находятся вне СО.
Поломки объектов не зависят друг от друга.
