Свойства показательного распределения разговора

Пусть - длина разговора - случайная величина, >0;

- функция распределения для .

- вещественное число – “возраст” разговора к данному моменту

- “остаток” разговора после момента , случайная величина

- функция распределения ( ) – вероятность того, что разговор, длившийся уже а единиц времени, продлится ещё >t единиц времени.

при : - безусловная вероятность,

при : - условная вероятность. Разговор уже продолжался уже «а» ед.времени.

Теорема(Свойство показательного закона):

Для того, чтобы остаток разговора был распределен также как и весь разговор , необходимо и достаточно, чтобы закон распределения являлся показательным.

~

Доказательство:

Достаточность. ; , не зависит от не зависит от . Следовательно, . Ч.т.д.

Замечания:

1. ~ остаток разговора распределен как и весь закон.

2. Остаток разговора не повлияет на весь разговор.

А) Если функции распределений случайных величин совпадают, то такие случайные величины отождествляются. ~ . Тогда - семейство случайных величин, зависящих от - случайный процесс.

Показательный закон играет исключительную роль среди всех законов распределения – только при показательном законе распределения остаток ведет себя так же, как и весь разговор.

, в момент вероятность закончиться у обоих разговоров

Б) ~ - часть ведет себя как целое.

В) ~ -беск.мало

2. Физический смысл показательного закона.

Длина разговора является бесконечно малой величиной. Большинство вызовов нуждается в кратковременном (близком к 0) обслуживании. Поскольку в реальности дело обстоит не так, эта предпосылка неверна. Тем не менее, предполагаем закон распределения показательным.

Со временем от этой предпосылки удалось отказаться.

3. Физический смысл параметра : -ср.число вызовов, кот.может быть обслужено или интенс. обсл

:

- средняя длина разговора; - интенсивность обслуживания вызовов на линии. Среднее число вызовов, которое происходит в ед. времени

- пропускная способность для СО

nBt-ср.число вызовов обслуживания за время t

4. Расчет (или 1/ ) в показательном законе.

А) Наблюдаем за случайной величиной

Б) Регистрируем ее реализации -фактическое время реализации в i-ом наблюдении.

В)ищем . 1/в-ср.длина разговора

Марковость в задаче Эрланга

Если входящий поток в данную СО – простейший, время обслуживания распределено по показательному закону, то случайный процесс 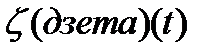(сост. СО на t) является Марковским.

Доказательство:

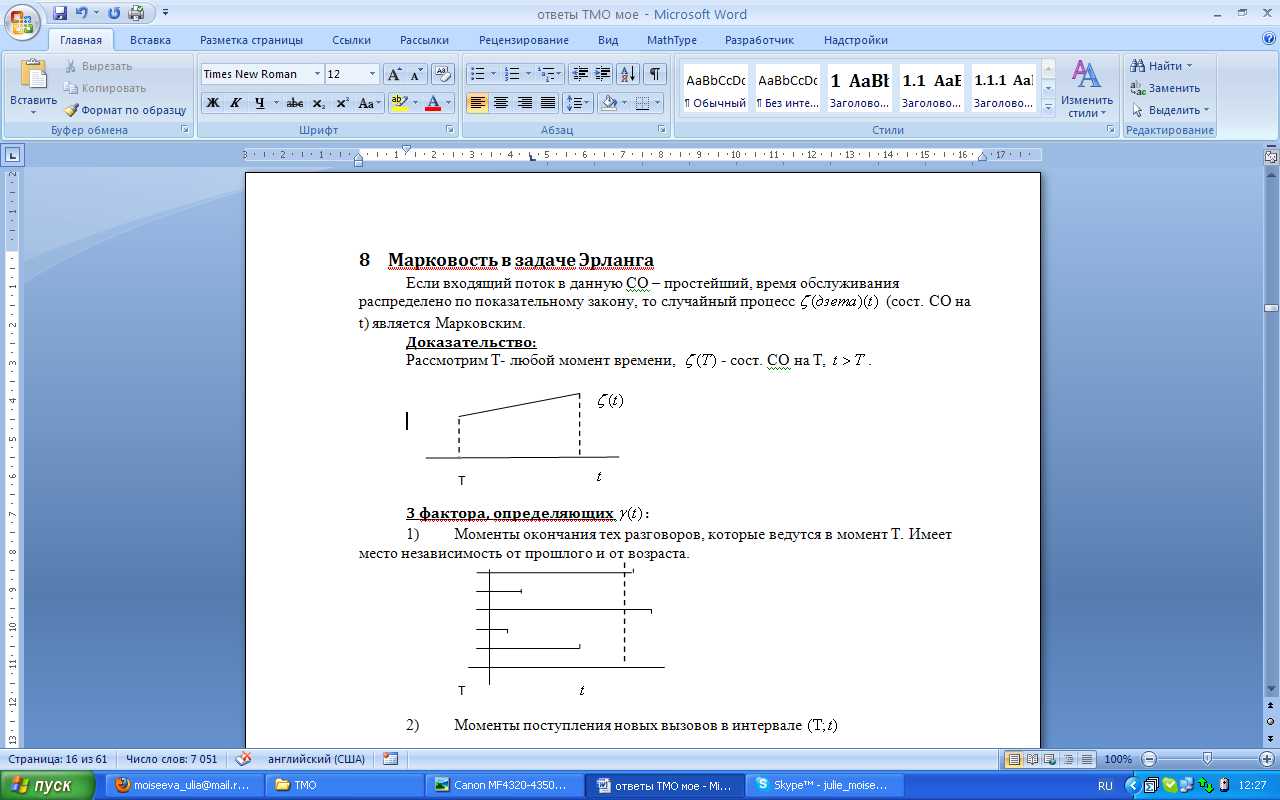
Рассмотрим T- любой момент времени, 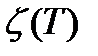- сост. СО на T, .

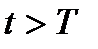Рассмотрим будущее значение. t>T, 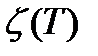-состояние

3 фактора, определяющих :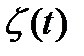

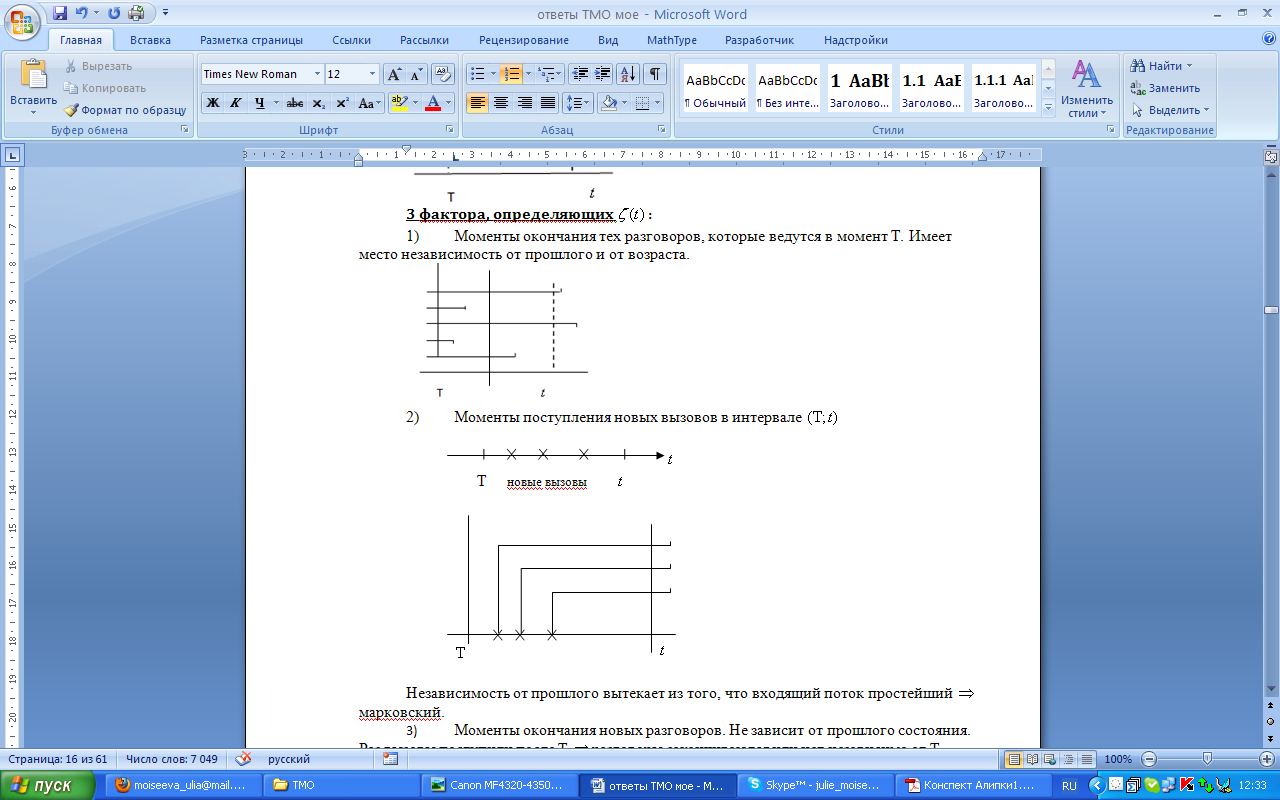
1) Моменты окончания тех разговоров, которые ведутся в момент T. Могут закончиться, а могут продолжаться.

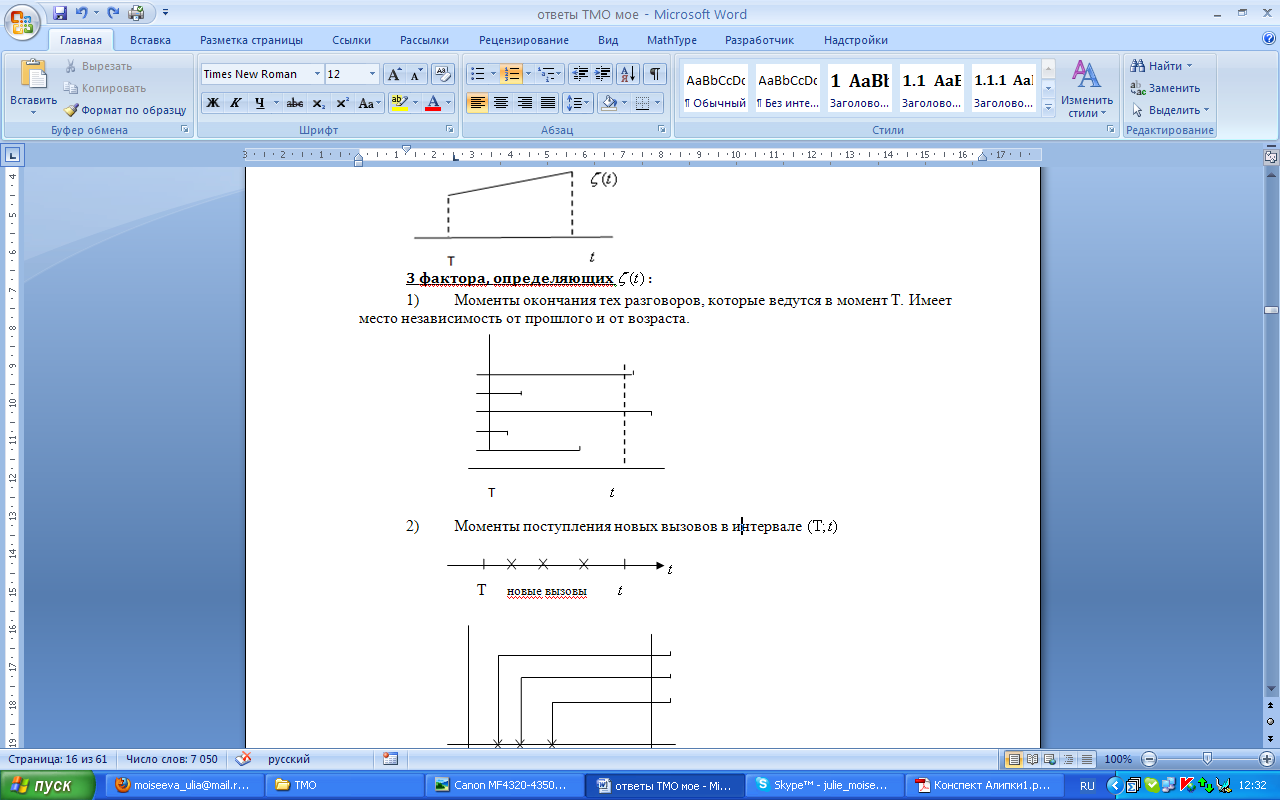
2) Моменты поступления новых вызовов в интервале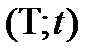

Независимость от прошлого вытекает из того, что входящий поток простейший марковский.

3) Моменты окончания новых разговоров. Не зависит от прошлого состояния. Раз вызовы поступили после T разговоры заканчиваются или нет независимо от T.

Для каждого фактора:

Для первого: из показательного закона, при котором возрастает разговор не влияет на окончание.

Для второго: это вытекает из предпосылки о простейшем потоке (явл.марковским

Для третьего: это самоопределение 3его фактора: они поступили в момент времени Т и не важно что было до!