Для направлений «менеджмент», «экономика» (вечернее отделение)

МАТЕМАТИКА

Для направлений «менеджмент», «экономика» (вечернее отделение)

И специальности «психология»

Часть 3

Теория вероятностей и математическая статистика

Учебно-методический комплекс

Авторы-составители

д.т.н., профессор А.Н. Данчул,

к.ф.-м.н., доцент Т.Е. Сафонова

Москва – 2008

Содержание

ОСНОВНЫЕ ПОЛОЖЕНИЯ.. 3

УЧЕБНО-ТЕМАТИЧЕСКИЙ ПЛАН.. 5

СОДЕРЖАНИЕ ТЕМ.. 5

ПЛАНЫ ПРАКТИЧЕСКИХ ЗАНЯТИЙ.. 8

ПЕРЕЧЕНЬ РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ.. 16

КОНТРОЛЬНЫЕ ЗАДАНИЯ.. 16

Таблица вариантов. 17

Контрольное задание. 18

ВОПРОСЫ К ЭКЗАМЕНУ.. 23

ПРИЛОЖЕНИЕ ОБРАЗЕЦ ОФОРМЛЕНИЯ ТИТУЛЬНОГО ЛИСТА КОНТРОЛЬНОГО ЗАДАНИЯ.. Ошибка! Закладка не определена.

ОСНОВНЫЕ ПОЛОЖЕНИЯ

Программа части 3 Теория вероятностей и математическая статистика учебной дисциплины «Математика» разработана в соответствии с требованиями Государственного образовательного стандарта профессионального высшего образования для обучения студентов бакалавриата по направлениям «менеджмент» и «экономика» (вечернее отделение) и специальности «психология».

Целью изучения дисциплины является подготовка студентов к творческому восприятию последующих общепрофессиональных и специальных дисциплин. Студенты должны научиться владеть современным математизированным профессиональным языком, принятым в мировом научном сообществе, знать основные возможности и ограничения применения математического аппарата в профессиональной деятельности, а также иметь базовые навыки использования математического инструментария.

Часть 3 Теория вероятностей и математическая статистика дисциплины «Математика» направлена на достижение вышеуказанных целей в области теории вероятностей и математической статистики.

Часть 3 Теория вероятностей и математическая статистика дисциплины «Математика» читается в III семестре, рассчитана на 102 часа занятий, из которых 24 часа – лекции, 26 часов – практические занятия (в том числе 10 часов на ПЭВМ) и 52 часа – самостоятельные занятия. Она требует освоения материалов частей 1 и 2 дисциплины «Математика»,прочитанных вI и II семестрах.

По части 3 Теория вероятностей и математическая статистика дисциплины «Математика» предусмотрено одно письменное контрольное задание, выполняемое во внеаудиторное время и одно контрольное задание с использованием Excel, задачи которого выполняются на каждом занятии, проводимом в компьютерном классе.

Формой итогового контроля работы студентов бакалавриата по направлениям «менеджмент» и «экономика» (вечернее отделение) является экзамен. В экзаменационный билет входят один теоретических вопроса и одна задача из числа включенных в планы практических занятий или контрольные задания. К экзамену допускаются студенты, выполнившие письменное контрольное задание и контрольное задание с использованием Excel.

Формой итогового контроля работы студентов специальности «психология» является зачет. На зачете проверяется знание одного-двух теоретических вопросов. К зачету допускаются студенты, выполнившие письменное контрольное задание и контрольное задание с использованием Excel.

Требования к уровню освоения дисциплины включают знание определений рассматриваемых понятий, понимание формулировок и идей доказательств используемых теорем, знание доказательств основных теорем, излагаемых на лекциях, уверенное владение методами решения задач, содержащихся в планах практических занятий.

УЧЕБНО-ТЕМАТИЧЕСКИЙ ПЛАН

№	Тема занятий	Всего часов	В том числе:
Лекции	Практич. занятия (из них в компьютерном классе)	Самост. работа
1.	Случайные события
2.	Случайные величины			10 (4)
3.	Стационарные случайные процессы
4.	Основы математической статистики			4 (2)
5.	Проверка статистических гипотез			2 (2)
6.	Регрессионный анализ. Элементы дисперсионного анализа			2 (2)
	ИТОГО:			26 (10)

СОДЕРЖАНИЕ ТЕМ

Тема 1. Случайные события

Основные понятия теории вероятностей. Случайные события. Вероятность события. Теоремы сложения вероятностей.

Условная вероятность. Теорема умножения вероятностей. Независимые события. Формула полной вероятности. Формула Байеса.

Повторные испытания. Формула Бернулли.

Тема 2. Случайные величины

Дискретные и непрерывные случайные величины. Функция распределения случайной величины. Плотность распределения непрерывной случайной величины. Числовые характеристики случайных величин: математическое ожидание, дисперсия, среднее квадратическое отклонение. Их свойства. Начальные и центральные моменты случайных величин.

Основные законы распределения случайных величин: равномерное, Бернулли, Пуассона, экспоненциальное, нормальное.

Неравенство Чебышева. Теорема Чебышева. Закон больших чисел. Центральная предельная теорема. Локальная и интегральная теоремы Муавра-Лапласа.

Многомерные случайные величины. Функция распределения и плотность двумерной случайной величины. Зависимые и независимые случайные величины. Условные законы распределения. Числовые характеристики двумерных случайных величин. Ковариация, коэффициент корреляции.

Тема 3. Случайные процессы

Случайные процессы. Функция распределения и плотность для случайного процесса. Характеристики случайных процессов.

Марковские процессы. Потоки событий. Цепи Маркова. Уравнения Чепмена-Колмогорова. Условие единственности и нахождение стационарных вероятностей для цепи Маркова.

Основные понятия теории массового обслуживания. Формулы Эрланга. Управление запасами.

ПЛАНЫ ПРАКТИЧЕСКИХ ЗАНЯТИЙ

Тема 1. Случайные события

Занятие 1.

1. Повторение определений основных понятий темы.

2. Решить задачи [Л1[1], с.34 – 35]:

1.17а; 1.18; 1.19.

3. Среди 25 студентов, из которых 15 девушек, разыгрываются 4 приглашения на дискотеку, причем каждый может выиграть только один билет. Какова вероятность того, что среди обладателей билета окажутся
а) только девушки, б) только юноши?

На дом

Какова вероятность того, что среди обладателей билета окажутся
две девушки и двое юношей?

4. Решить задачи [Л1, с.61 – 62]:

1.37; 1.43; 1.45 на дом 1.38; 1.45; 1.51.

5. В одной группе Г₁ студентов, из которых О₁ учатся на «отлично». В другой – Г₂ студентов, из которых на «отлично» учатся О₂. Из каждой группы случайным образом выбрали по одному студенту. Какова вероятность того, что оба учатся на «отлично»?

а) Г₁=18; О₁=9; Г₂=16; О₂=4

На дом

б) Г₁=15; О₁=5; Г₂=20; О₂=6.

6. Решить задачи [Л1, с.45, 63]:

1.26а-б; 1.55 на дом 1.26в-д; 1.56.

Занятие 2.

1. Повторение определений основных понятий темы.

2. В семье двое детей. Известно, что один из них мальчик. Какова вероятность, что оба ребенка – мальчики?

3. По результатам проверки зачетных работ оказалось, что в первой группе получили зачет 20 студентов из 30, а во второй 16 из 32. Какова вероятность того, что наудачу выбранная зачтенная работа принадлежит студенту первой группы?

4. Решить задачи [Л1, с.49, 64-65]:

1.31а; 1.65; 1.69 на дом 1.33а; 1.70; 1.82.

5.Два стрелка сделали по одному выстрелу в одну и ту же мишень. Вероятность попадания в мишень для первого стрелка равна 0,6, а для второго – 0,4. В мишени оказалась одна пробоина. Найти вероятность того, что пробоина принадлежит первому стрелку.

На дом

Два стрелка сделали по одному выстрелу в одну и ту же мишень. Вероятность попадания в мишень для первого стрелка равна 0,8, а для второго – 0,5. В мишени оказалась одна пробоина. Найти вероятность того, что пробоина принадлежит второму стрелку.

Занятие 3

1. Повторение определений основных понятий темы.

2. Решить задачи [Л1, с. 53, 64-67]:

1.34; 1.72; 1.78; 1, 85; 1.98 на дом 1.73; 1.75; 1.87; 1.95; 1.97.

3. Вероятность, что малое предприятие станет банкротом в течение года равна 0,2. Найти вероятность, что из восьми малых предприятий за первый год обанкротятся два предприятия.

На дом

Найти вероятность, что из восьми малых предприятий за первый год обанкротятся более двух предприятий.

Тема 2. Случайные величины

Занятие 1

1. Повторение определений основных понятий темы.

2. Решить задачи [Л1, с.90-92]:

3.2; 3.3.

Построить функцию распределения, найти математическое ожидание, дисперсию и среднеквадратическое отклонение исходных и полученных случайных величин.

3. Решить задачи [Л1, с.133-137]:

3.25; 3.28; 3.31; 3.52 на дом 3.26; 3.29; 3.34; 3.54.

Занятие в компьютерном классе 1

1. Повторение определений основных понятий темы.

2. Построение и анализ графиков плотностей распределений и функций распределений Бернулли, Пуассона, Фишера, Стьюдента, экспоненциального и нормального с использованием стандартных функций Excel (БИНОМ РАСП, ПУАССОН, FРАСП, СТЬЮДРАСП, ЭКСПРАСП, НОРМРАСП).

3. Нахождение критических значений различных распределений для разных уровней значимости (КРИТБИНОМ, FРАСПОБР, СТЬЮДРАСПОБР, НОРМОБР).

4. Использование нормализованных значений, определение квантилей (НОРМАЛИЗАЦИЯ)

Практическое контрольное задание

1. Построить и сравнить графики плотностей распределения и функций распределений хи-квадрат с числом степеней свободы 5 и 3 на интервале (0, 10).

2. Найти критические значения этих распределений для уровней значимости 0,05 и 0,01.

Занятие 2

1. Повторение определений основных понятий темы.

2. Клиенты банка, не связанные друг с другом, не возвращают кредиты в срок с вероятностью 0,1. Составить закон распределения числа возвращенных в срок кредитов из числа выданных. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение числа возвращенных кредитов.

3. Решить задачи [Л1, с.135-140]:

3.36; 3.41; 3.49; 3.58; 3.64 на дом 3.43; 3.50; 3.57; 3.59; 3.65; 3.72

Занятие в компьютерном классе 2

1. Повторение определений основных понятий темы.

2. Случайные величины X и Y независимы и имеют один и тот же закон распределения.

Значение
Вероятность	0,2	0,3	0,5

Составить закон распределения случайной величины Z=2X. Найти математическое ожидание и среднее квадратическое отклонение случайных величин X, Y, Z.

3. Решить задачи [Л1, с. 214]:

5.10; 5.18, 5.23/

4. В ходе эксперимента измерялись характеристики x и y. Представить результаты графически. Найти коэффициент корреляции. Что можно сказать о зависимости этих двух величин?

x	0,8	1,0	2,7	3,4	0,3	-0,3	-0,6	-0,5	1,0	-2,0
y	-1,0	0,4	-0,1	-0,4	-1,6	0,3	0,8	0,9	0,0	-0,5

Практическое контрольное задание

1. Составить закон распределения случайной величины W=X+Y (см. таблицу п.2). Найти математическое ожидание и среднее квадратическое отклонение случайной величины W.

Занятие 3

1. Повторение определений основных понятий темы.

2. В группе обучается 36 студентов. Вероятность того, что день рождения студента приходится на определенный день года, равна 1/365. Оценить вероятность того, что, по крайней мере 2 студента имеют одинаковый день рождения.

3. В институте обучается 730 студентов. Вероятность того, что день рождения студента приходится на определенный день года, равна 1/365. Найти наиболее вероятное число студентов, родившихся 1 января, оценить вероятность такого события. Оценить вероятность того, что, по крайней мере, 3 студента имеют одинаковый день рождения.

4. Фирма раскладывает рекламные листки по почтовым ящикам. Прежний опыт работы показывает, что на 500 рекламных листков приходится один заказ. Оценить вероятность того, что при размещении 25 тысяч листков число заказов будет равно 48.

На дом

Оценить вероятность того, что при размещении 25 тысяч листков число заказов будет находиться в пределах от 45 до 55.

5. Решить задачи [Л1, с. 172 – 174]:

4.14; 4.19 на дом 4.18; 4.21; 4.28

Тема 3. Случайные процессы

1. Повторение определений основных понятий темы.

2. Решить задачи [Л1, с. 241 – 264]:

7.1; 7.1а; 7.3; 7.4; 7.13; 7.15 на дом 7.10; 7.14.

Тема 4. Основы математической статистики

Занятие 1

1. Повторение определений основных понятий темы.

2. В городе работает N=30000 человек. При выборочном опросе n=600работающих оказалось, что k=200 из них имеют высшее образование. Найти

а)вероятность того, что доля людей с высшим образованию среди всех работающих города отличается от выборочной не более чем на 10%;

б) границы доверительного интервала для числа работающих с высшим образованием (для доверительных вероятностей, равных 0,95 и 0,99).

На дом

Решить задачу 2 при N=40000, n=1000, k=400.

3. Решить задачи [Л1, с.327 – 329]:

9.19; 9.23; 9.26; 9.32 на дом 9.20; 9.25; 9.33.

Занятие в компьютерном классе

1. Повторение определений основных понятий темы.

2. Решить с использованием мастера функций и пакета анализа задачу 8.10, 8.13 [Л1, с.285].

Практическое контрольное задание

1. Решить с использованием мастера функций и пакета анализа задачу 8.11 [Л1, с.285].

Тема 5. Проверка статистических гипотез

Занятие в компьютерном классе

1. Повторение определений основных понятий темы.

2. Для проверки эффективности новой системы оплаты труда отобраны две группы рабочих. В первой группе применялась новая система, а во второй – нет. Результаты выборочного эксперимента приведены в таблице. На уровне значимости 0,05 выяснить влияние новой системы оплаты труда на производительность.

Группа	Численность	Выборочная средняя выработка	Выборочная дисперсия выработки

3. В двух группах, различающихся базовым образованием, проводилось психологическое тестирование, в результате которого была получена некоторая интегральная характеристика каждого испытуемого, измеряемая в баллах и принимающая значение от 100 до 400. В группе с гуманитарным образованием оказалось 12 человек, у которых эта характеристика имела значение от 100 до 200, 14 – от 200 до 300 и 5 – больше 300. В группе с техническим образованием оказалось 16 человек, у которых эта характеристика имела значение от 100 до 200, 7 – от 200 до 300 и 6 – больше 300.

Зависит ли исследуемая характеристика от типа образования? Ответ обосновать с использованием критерия хи-квадрат.

4. Решить c использованием формул, мастера функций и надстройки «пакет анализа данных» задачи 10.17; 10.26 [Л1, с.375 – 377].

Практическое контрольное задание

Решить c использованием формул и мастера функций задачу 10.19 [Л1, с.285].

Тема 6. Регрессионный анализ. Элементы дисперсионного анализа

Занятие в компьютерном классе

1. Повторение определений основных понятий темы.

2. Решить c использованием формул, мастера диаграмм и надстройки «пакет анализа данных» задачи 13.9; 11.4 [Л1, с.476, 393].

Практическое контрольное задание

Решить c использованием формул, мастера диаграмм и надстройки «пакет анализа данных» задачу 12.15 [Л1, с.437].

КОНТРОЛЬНЫЕ ЗАДАНИЯ

Выполняется одно домашнее контрольное задание, состоящее из 6 задач. По выданному преподавателем номеру варианта задания с помощью таблицы вариантов, приведенной на следующей странице, определяются номера вариантов входящих в задание задач. Образец оформления титульного листа задания приведен в Приложении.

Срок сдачи задания – 10 неделя (до 8 ноября).

Срок зачета задания (с учетом исправления ошибок) – 11 неделя (до 15 ноября).

Контрольное задание с использованием Excel выполняется на занятиях, проводимых в компьютерном классе.

Таблица вариантов

Задача
№ варианта задания	Номера вариантов задач
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.

Контрольное задание

Задача 1. Бросают два кубика. Суммируют число очков, выпавших на верх­них гранях кубиков. Построить множество элементарных событий W и его подмножество, соответствующее указанному событию А. Найти вероятность события А. Построить подмножество, соответствующее событию 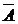(дополнение А). Найти его вероятность.

Вариант	Событие А
	А={сумма очков больше 3}
	А={сумма очков больше 4}
	А={сумма очков больше 5}
	А={сумма очков больше 6}
	А={сумма очков больше 7}
	А={сумма очков больше 8}
	А={сумма очков больше 9}
	А={сумма очков больше 10}
	А={сумма очков больше 11}
	А={сумма очков больше 2}

Задача 2. В одном сосуде находятся Б₁ белых и Ч₁ черных шаров. Во втором – Б₂ белых и Ч₂ черных. Бросают два кубика. Если сумма очков, выпавших на верхних гранях, меньше 10, берут шар из первого сосуда, если больше или равна 10 – из второго.

Вариант
	Б1=7; Ч1=6; Б2=5; Ч2=9	Вынут белый шар. Какова вероятность того, что сумма очков была не меньше 10?
	Б1=7; Ч1=5; Б2=6; Ч2=9	Вынут черный шар. Какова вероятность того, что сумма очков была меньше 10?
	Б1=6; Ч1=5; Б2=7; Ч2=9	Вынут белый шар. Какова вероятность того, что сумма очков была меньше 10?
	Б1=7; Ч1=5; Б2=9; Ч2=6	Вынут черный шар. Какова вероятность того, что сумма очков была не меньше 10?
	Б1=5; Ч1=6; Б2=9; Ч2=6	Вынут черный шар. Какова вероятность того, что сумма очков была не меньше 10?
	Б1=5; Ч1=9; Б2=7; Ч2=6	Вынут белый шар. Какова вероятность того, что сумма очков была меньше 10?
	Б1=5; Ч1=7; Б2=6; Ч2=9	Вынут черный шар. Какова вероятность того, что сумма очков была не меньше 10?
	Б1=5; Ч1=7; Б2=9; Ч2=6	Вынут белый шар. Какова вероятность того, что сумма очков была меньше 10?
	Б1=4; Ч1=8; Б2=9; Ч2=6	Вынут белый шар. Какова вероятность того, что сумма очков была меньше 10?
	Б1=8; Ч1=4; Б2=6; Ч2=9	Вынут черный шар. Какова вероятность того, что сумма очков была не меньше 10?

Задача 3.Случайная величина X задана плотностью распределения вероятностей (см. график). Построить график функции распределения вероятностей, найти математическое ожидание и дисперсию случайной величины.

Вариант	a	b	c	d	Вариант	a	b	c	d
		0,3	1,15	0,5			1,7	2,28	0,6
		0,6	1,3	0,5				2,6	0,4
		0,5	1,25	0,5			2,5	3,3	0,4
	0,5		1,7	0,6				3,6	0,4
		1,5	2,2	0,6				4,4	0,6

Задача 4. Найти стационарные вероятности и стационарное математичес­кое ожидание для марковского процесса N, заданного графом переходов состояний.

Варианты 1 – 3.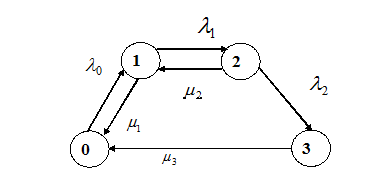
Варианты 4 – 6.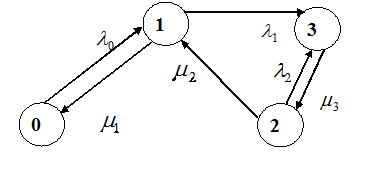
Варианты 7 – 10.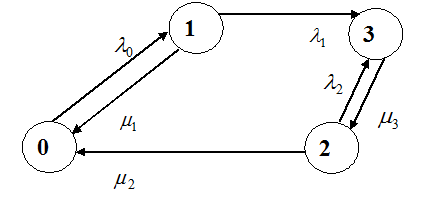

Вариант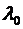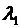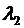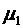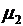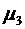

Задача 5. Закон распределения двумерной дискретной случайной величины (X, Y) задан таблицей:

Y
X
-1	0,02	0,03	0,09	0,01
	0,04	0,2	0,16	0,1
	0,05	0,1	0,15	0,05

Найти условные законы распределения:

Вариант
	случайной величины X при условии Y=0 и случайной величины Y при условии X=-1
	случайной величины X при условии Y=0 и случайной величины Y при условии X=0
	случайной величины X при условии Y=0 и случайной величины Y при условии X=1
	случайной величины X при условии Y=1 и случайной величины Y при условии X=1
	случайной величины X при условии Y=1 и случайной величины Y при условии X=0
	случайной величины X при условии Y=1 и случайной величины Y при условии X=-1
	случайной величины X при условии Y=2 и случайной величины Y при условии X=-1
	случайной величины X при условии Y=3 и случайной величины Y при условии X=0
	случайной величины X при условии Y=2 и случайной величины Y при условии X=1
	случайной величины X при условии Y=3 и случайной величины Y при условии X=1

Задача 6. Перед выборами в городе было опрошено n человек. Из них k человек отдали предпочтение нынешнему мэру. На какое количество голосов может рассчитывать мэр на выборах, если всего в городе N избирателей (вычислить с доверительной вероятностью 0,95 и 0,99)?

Вариант
	n=500; k=200; N=30000
	n=1200; k=300; N=80000
	n=800; k=200; N=100000
	n=600; k=150; N=50000
	n=700; k=140; N=90000
	n=900; k=300; N=78000
	n=750; k=250; N=100000
	n=1200; k=400; N=960000
	n=900; k=150; N=750000
	n=690; k=230; N=90000

ВОПРОСЫ К ЭКЗАМЕНУ (ЗАЧЕТУ)

1. Основные понятия теории вероятностей. Пространство элементарных событий.

2. Основные формулы для вычисления вероятностей.

3. Независимые и зависимые события. Условная вероятность.

4. Формула полной вероятности.

5. Теорема Байеса.

6. Формула Бернулли.

7. Определение случайной величины. Дискретные и непрерывные случайные величины.

8. Функция распределения случайной величины. Плотность распределения непрерывной случайной величины.

9. Числовые характеристики случайных величин: математическое ожидание, дисперсия, среднее квадратическое отклонение.

10. Неравенство Чебышева.

11. Теорема Чебышева. Закон больших чисел.

12. Локальная и интегральная теоремы Муавра-Лапласа.

13. Функция распределения и плотность двумерной случайной величины.

14. Зависимые и независимые случайные величины. Условные законы распределения.

15. Числовые характеристики двумерных случайных величин.

16. Случайные процессы. Функция распределения и плотность.

17. Характеристики случайных процессов.

18. Марковские процессы.

19. Потоки событий.

20. Цепи Маркова. Уравнения Чепмена-Колмогорова.

21. Генеральная совокупность и выборка, вариационный ряд, полигон частот, гистограмма, эмпирическая функция распределения.

22. Числовые характеристики выборочного распределения.

23. Понятие об оценке параметров. Характеристики оценок.

24. Методы нахождения оценок: метод моментов, метод максимального правдоподобия, метод наименьших квадратов.

25. Понятие об интервальной оценке параметров. Доверительная вероятность и доверительный интервал.

26. Понятие и общая схема проверки статистической гипотезы.

27. Проверка гипотез о равенстве средних двух совокупностей.

28. Проверка гипотез об однородности выборок.

29. Линейная парная регрессия. Коэффициент корреляции.

30. Проверка гипотез о зависимости переменных.

31. Однофакторный дисперсионный анализ.

ПРИЛОЖЕНИЕ
ОБРАЗЕЦ ОФОРМЛЕНИЯ ТИТУЛЬНОГО ЛИСТА
КОНТРОЛЬНОГО ЗАДАНИЯ

Российская академия государственной службы при Президенте РФ

Задание № 1 по математике

Слушателя группы О-811

Иванова Петра Фомича

Вариант 15

№ задачи
№ варианта задачи
Отметка о решении

Г.

[1] Л1 – литература под номером 1 в списке литературы

МАТЕМАТИКА

для направлений «менеджмент», «экономика» (вечернее отделение)