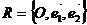Уравнения прямой в аффинной системе координат

Уравнение множества точек

Положение точки в плоскости чаще всего описывается в декартовой прямоугольной системе координат парой чисел М(x;y).

Описание линии, в частности прямой, можно было бы строить путем описания каждой ее точки, однако это очень затруднительно ввиду того, что точек бесконечно много.

Если имеем уравнение

, (12.1)

то все точки разбиваются на два класса: 1) точки, координаты которых удовлетворяют уравнению, 2) точки, координаты которых не удовлетворяют уравнению. Точки первого класса образуют множество F, а уравнение (1) называется уравнением множества точек F.

Если уравнение (1) – многочлен первого и второго порядка, например, 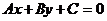или 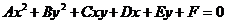, то такие множества – объект изучения аналитической геометрии. Если уравнение (1) – многочлен произвольного порядка степени, большей второй, то такие множества – объект изучения алгебраической геометрии. Если уравнение (1) – любая другая функция, то такие множества – объект изучения дифференциальной геометрии.

Уравнение называется также неявным уравнением. Если уравнение (12.1) можно разрешить относительно одной координаты, например, у,

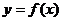, (12.2)

где х – независимое переменное, у – зависимое, то множество называется графиком функции, а уравнение (12.2) – явным уравнением. Если обе координаты х и у задаются с помощью вспомогательного переменного – параметра t (или нескольких параметров),

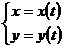(12.3)

то уравнения (12.3) называются параметрическими уравнениями множества F.

Уравнение прямой связывает между собой координаты точки, принадлежащей прямой. Из курса планиметрии известно, что через две точки плоскости можно провести единственную прямую (аксиома планиметрии). На языке алгебры это означает, что, записать уравнение прямой можно, зная координаты двух ее точек, т.е. два условия. Если же известна только одна точка прямой, то для составления уравнения требуется задать еще одно условие, например, вектор, параллельный прямой. В этом случае можно записать уравнение прямой, называемое каноническим, а также параметрические уравнения. Если кроме точки искомой прямой известен вектор, перпендикулярный прямой, то можно записать общее уравнение. Если известны отрезки, отсекаемые прямой на осях координат, то можно записать так называемое уравнение«в отрезках». Если в прямоугольной системе координат известен отрезок, отсекаемый на оси ординат (начальная ордината) и угол наклона (тангенс угла наклона) прямой к оси абсцисс, получим уравнение с угловым коэффициентом. Если известен угол между перпендикуляром к прямой и осью абсцисс, расстояние от начала координат до прямой, можно записать нормальное (нормированное) уравнение. Все уравнения получаются из наглядных геометрических соображений.

Уравнения прямой в аффинной системе координат

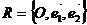
Определение 1.

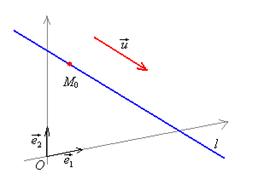
Вектор, отличный от нулевого, параллельный искомой прямой, называется направляющим вектором прямой.

Точка плоскости М принадлежит прямой l, если координаты точки удовлетворяют уравнению прямой. На языке векторов это означает, что, где бы ни лежала точка М на прямой l, вектор 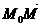коллинеарен вектору .

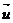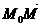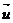|| , или,

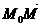=t 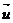. (12.4)

Откуда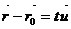

Получили векторное уравнение прямой: 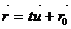(12.5)

Откуда 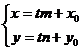(12.6)

– параметрические уравнения прямой, где t – параметр.

Условие коллинеарности векторов: координаты 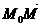, 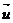пропорциональны. Если 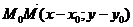, , 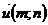то.

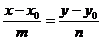(12.7)

Это уравнение связывает координаты точки М₀, вектора 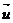и произвольной точки М прямой l. Оно называется каноническим уравнением прямой.

Условие коллинеарности векторов 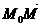, 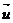можно записать в форме определителя, используя свойство: определитель с пропорциональными строками равен нулю, т.е.

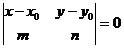(12.8)

Это уравнение прямой в форме определителя. Откуда

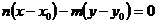, (12.9)

Коэффициенты m и n одновременно не обращаются в нуль, т.к. 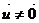. Из уравнения (12.9) вытекают следствия:

1. Если l || 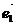(1;0) , то уравнение примет вид 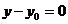(прямая параллельна оси Ох).

2. Если l || 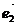(0;1) , то уравнение примет вид 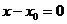(прямая параллельна оси Оу).

3. Если прямая не параллельная осям, тогда выразим :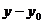

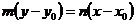
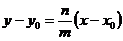, (12.10)

где 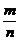– угловой коэффициент прямой в данной системе координат.

Общее уравнение прямой

Раскроем определить (12.8):

.

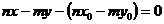Введем обозначения: n=A, –m=B, 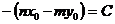. Получим уравнение:

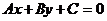(12.12)

Следствие. Так как 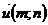, то 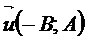. (12.13)

Определение 2.

Уравнение 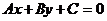называется общим уравнением прямой.

Уравнения прямой

Определение 3.

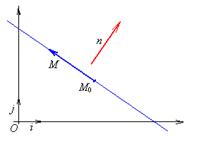Вектор, перпендикулярный (ортогональный) прямой, называется нормальным вектором прямой или вектором нормали.

Дано: 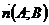, М₀(х;у).

Составить уравнение прямой l / М₀Îl , l^ .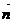

Решение.

Пусть М – точка произвольная прямой l. Рассмотрим векторы 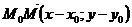и 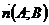. 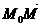– направляющий вектор прямой, 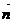– перпендикулярный к ней вектор. Тогда 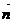^ 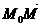, т.е. 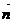× 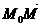=0 (1),

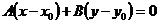(12.14)

Это уравнение прямой, проходящей через данную точку перпендикулярно данному вектору.

Таким образом, геометрический смысл общего уравнения прямой Ах+Ву+С=0 заключается в том, что коэффициенты А,В – суть координаты векторов:

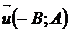– направляющий вектор. (12.15)

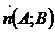– перпендикулярный вектор. (12.16)

Определение 4.

Нормированным уравнением прямой называется общее уравнение А₀х+В₀у+С₀=0, для которого 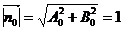. Множитель 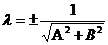называется нормирующим множителем.

Определение 5.

Нормированное уравнение прямой называется нормальным, если свободный член в нем отрицателен.

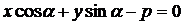(12.17)

Так как геометрический смысл координат орта вектора: 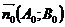= = 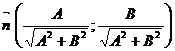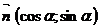, то для того чтобы получить из общего уравнения прямой нормальное уравнение, нужно разделить длину вектора нормали, взятую со знаком, противоположным знаку свободного члена.

Пример 2. Составим нормальное уравнения прямой АВ, если А(1;–2), В(0;5).

Решение. 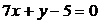– общее уравнение прямой АВ (см. пример 1):

Из уравнения вектор 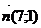, тогда 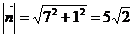, разделим все члены уравнения на длину вектора нормали: 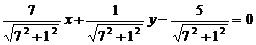, откуда получим – нормированное уравнение.

Т.к. свободный член отрицателен, то это и нормальное уравнение прямой АВ.

Пример 3. Составим уравнения медианы АМ и высоты АН Dтреугольника АВС, если А(1;–2), В(0;5), С(–1;3).

Решение.

1) Так как М – середина ВС, то координаты точки М (–0,5; 4).

Составим уравнение АМ: 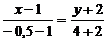, т.е. .

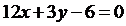2) Составим уравнение АН, проходящей через точку А перпендикулярно вектору 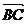(–1;–2): 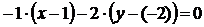или .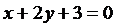

Угол между прямыми

Пусть даны прямые 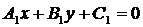и .

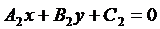Угол между прямыми: 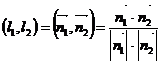, тогда

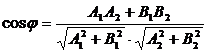(12.23)

Условие перпендикулярности прямых, заданных общими уравнениями:

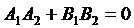(12.24)

Условие параллельности прямых, заданных уравнениямиy=k₁x+b₁ и y=k₂x+b₂:

k₁×k₂=–1 (12.25)

Пример 4. Вычислим угол А треугольника АВС, если А(1;–2), В(0;5), С(–1;3).

Решение.

Угол А – это угол между прямыми АВ и АС. Составим общие уравнения прямых:

прямая АВ: 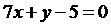; прямая АС: .

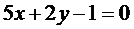Вычислим угол А: 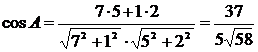»0,9717, ÐА»14^о.

Пример 5. Вычислим длину высоты АН DАВС, если А(1;–2), В(0;5), С(–1;3).

Решение. Длина высоты АН – расстояние от точки А до стороны ВС.

Составим уравнение ВС: , .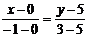

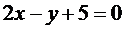Вычислим расстояние: .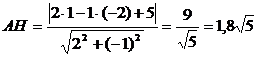

4.3. Геометрический смысл знака трехчлена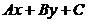

Множество всех точек М, координаты которых обращают трехчлен 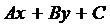в нуль, есть прямая, заданная общим уравнением, т.е.

l: 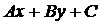=0.

Прямая делит плоскость на две полуплоскости и 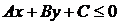(с границей). Геометрический смысл знака трехчлена 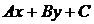состоит в том, что для всех точек одной полуплоскости, границей которой является прямая l: 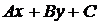=0, этот знак один и тот же. Для того, чтобы установить, лежат ли точки по одну и ту же сторону от прямой или же по разные стороны от нее, достаточно подставить их координаты в трехчлен и сравнить знаки полученных результатов.

Домашнее задание. Заполнить таблицу по образцу:

Условие	Уравнение	Название уравнения
Аффинная система координат
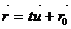		векторное
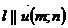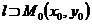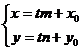,		параметрические
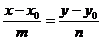		каноническое
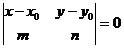		в форме определителя
		общее
		в отрезках
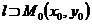		прямой, проходящей через две точки
Прямоугольная система координат
		прямой, проходящей данную точку перпендикулярно данному вектору
		с угловым коэффициентом
		нормированное
		нормальное

Уравнение множества точек

Положение точки в плоскости чаще всего описывается в декартовой прямоугольной системе координат парой чисел М(x;y).

Описание линии, в частности прямой, можно было бы строить путем описания каждой ее точки, однако это очень затруднительно ввиду того, что точек бесконечно много.

Если имеем уравнение

, (12.1)

то все точки разбиваются на два класса: 1) точки, координаты которых удовлетворяют уравнению, 2) точки, координаты которых не удовлетворяют уравнению. Точки первого класса образуют множество F, а уравнение (1) называется уравнением множества точек F.

Если уравнение (1) – многочлен первого и второго порядка, например, 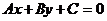или 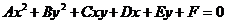, то такие множества – объект изучения аналитической геометрии. Если уравнение (1) – многочлен произвольного порядка степени, большей второй, то такие множества – объект изучения алгебраической геометрии. Если уравнение (1) – любая другая функция, то такие множества – объект изучения дифференциальной геометрии.

Уравнение называется также неявным уравнением. Если уравнение (12.1) можно разрешить относительно одной координаты, например, у,

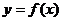, (12.2)

где х – независимое переменное, у – зависимое, то множество называется графиком функции, а уравнение (12.2) – явным уравнением. Если обе координаты х и у задаются с помощью вспомогательного переменного – параметра t (или нескольких параметров),

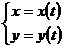(12.3)

то уравнения (12.3) называются параметрическими уравнениями множества F.

Уравнение прямой связывает между собой координаты точки, принадлежащей прямой. Из курса планиметрии известно, что через две точки плоскости можно провести единственную прямую (аксиома планиметрии). На языке алгебры это означает, что, записать уравнение прямой можно, зная координаты двух ее точек, т.е. два условия. Если же известна только одна точка прямой, то для составления уравнения требуется задать еще одно условие, например, вектор, параллельный прямой. В этом случае можно записать уравнение прямой, называемое каноническим, а также параметрические уравнения. Если кроме точки искомой прямой известен вектор, перпендикулярный прямой, то можно записать общее уравнение. Если известны отрезки, отсекаемые прямой на осях координат, то можно записать так называемое уравнение«в отрезках». Если в прямоугольной системе координат известен отрезок, отсекаемый на оси ординат (начальная ордината) и угол наклона (тангенс угла наклона) прямой к оси абсцисс, получим уравнение с угловым коэффициентом. Если известен угол между перпендикуляром к прямой и осью абсцисс, расстояние от начала координат до прямой, можно записать нормальное (нормированное) уравнение. Все уравнения получаются из наглядных геометрических соображений.

Уравнения прямой в аффинной системе координат