Проверка гипотезы о равенстве дисперсий двух нормально распределенных случайных величин.
Определение. Случайная величина Fmn называется распределенной по закону Фишера со степенями свободы m и n, если она представляется в виде
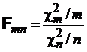 ,
,
где 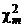 и
и 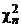 – независимые случайные величины, распределенные по закону c2 с m и n степенями свободы соответственно.
– независимые случайные величины, распределенные по закону c2 с m и n степенями свободы соответственно.
Рассмотрим две независимые случайные величины x и h, распределенные по нормальному закону с дисперсиями 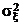 и
и 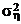 , которые предполагаются неизвестными. Пусть в результате наблюдений получены выборка
, которые предполагаются неизвестными. Пусть в результате наблюдений получены выборка 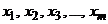 значений x и выборка
значений x и выборка 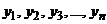 значений h,
значений h, 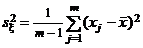 и
и 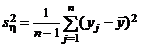 – исправленные выборочные дисперсии, соответствующие этим выборкам. Обозначим
– исправленные выборочные дисперсии, соответствующие этим выборкам. Обозначим
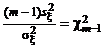 и
и 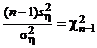 , (1)
, (1)
тогда 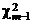 и
и 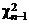 – случайные величины, распределенные по закону c2 со степенями свободы соответственно m – 1 и n – 1 (см. § 2, п. 3 (в)). Из независимости x и h следует, что случайные величины (1) также независимы. В соответствии с определением случайная величина
– случайные величины, распределенные по закону c2 со степенями свободы соответственно m – 1 и n – 1 (см. § 2, п. 3 (в)). Из независимости x и h следует, что случайные величины (1) также независимы. В соответствии с определением случайная величина
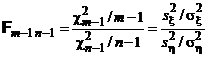 (2)
(2)
распределена по закону Фишера со степенями свободы m – 1 и n – 1.
Теперь мы можем построить критерий для проверки гипотезы H0: 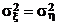 .
.
Если эта гипотеза верна, то из (2) получаем
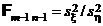 . (3)
. (3)
Случайную величину (3) и используют в качестве критерия для проверки гипотезы H0. Рассмотрим
Случай 1: 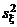 и
и 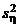 заметно различаются и при этом
заметно различаются и при этом 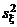 >
> 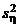 . В этом случае используется альтернативная гипотеза HА:
. В этом случае используется альтернативная гипотеза HА: 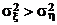 . Вычисляют
. Вычисляют 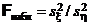 , затем по таблице критических точек распределения Фишера по уровню значимости a и числам степеней свободы m – 1 и n – 1 отыскивается критическая точка Fкр(a, m – 1, n – 1).
, затем по таблице критических точек распределения Фишера по уровню значимости a и числам степеней свободы m – 1 и n – 1 отыскивается критическая точка Fкр(a, m – 1, n – 1).
Если Fнабл < Fкр, то основную гипотезу принимают; если же Fнабл > Fкр, то основную гипотезу отвергают.
Если 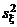 <
< 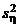 , то можно аналогично использовать левостороннюю критическую область, но обычно, поскольку таблица не содержит соответствующих критических точек, снова используют правостороннюю критическую область, взяв в качестве критерия обратное отношение
, то можно аналогично использовать левостороннюю критическую область, но обычно, поскольку таблица не содержит соответствующих критических точек, снова используют правостороннюю критическую область, взяв в качестве критерия обратное отношение 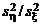 .
.
Случай 2: 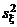 и
и 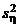 различаются мало, тогда в качестве альтернативной берется гипотеза HА:
различаются мало, тогда в качестве альтернативной берется гипотеза HА: 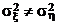 . По уровню значимости a/2 и числам степеней свободы m – 1 и n – 1 (m – 1 – число степеней свободы распределения с бóльшей выборочной дисперсией) ищут
. По уровню значимости a/2 и числам степеней свободы m – 1 и n – 1 (m – 1 – число степеней свободы распределения с бóльшей выборочной дисперсией) ищут 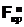 (a / 2, m – 1, n – 1), а затем
(a / 2, m – 1, n – 1), а затем 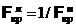 .
.
Если 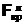 < Fнабл <
< Fнабл < 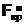 , основную гипотезу принимают, а при Fнабл <
, основную гипотезу принимают, а при Fнабл < 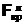 или Fнабл >
или Fнабл > 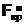 ее отвергают.
ее отвергают.
Пример 1. Получены выборки значений двух независимых случайных величин, распределенных по нормальному закону. Объемы выборок m = 11 и n = 14, исправленные выборочные дисперсии 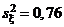 и
и 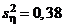 . Требуется проверить при уровне значимости a = 0,05 гипотезу H0: Dx = Dh при альтернативной гипотезе HA: Dx ¹ Dh.
. Требуется проверить при уровне значимости a = 0,05 гипотезу H0: Dx = Dh при альтернативной гипотезе HA: Dx ¹ Dh.
Здесь 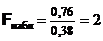 . По таблице критических точек распределения Фишера находим
. По таблице критических точек распределения Фишера находим 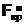 (0,025; 10; 13) = 3,25, откуда
(0,025; 10; 13) = 3,25, откуда 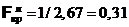 . Так как
. Так как 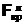 < Fнабл <
< Fнабл < 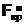 , то нет оснований отвергать гипотезу о равенстве дисперсий. Другими словами, выборочные дисперсии различаются незначимо.
, то нет оснований отвергать гипотезу о равенстве дисперсий. Другими словами, выборочные дисперсии различаются незначимо.
Пример 2. По двум выборкам, объемы которых m = 10 и n = 18, найдены исправленные выборочные дисперсии 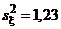 и
и 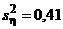 . При уровне значимости a = 0,05 требуется проверить гипотезу H0: Dx = Dh, взяв в качестве альтернативной гипотезу HA: Dx > Dh.
. При уровне значимости a = 0,05 требуется проверить гипотезу H0: Dx = Dh, взяв в качестве альтернативной гипотезу HA: Dx > Dh.
Здесь критическая область является правосторонней. По таблице критических точек распределения Фишера находим критическую точку: 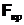 (0,05; 9; 17) = 2,50. Поскольку
(0,05; 9; 17) = 2,50. Поскольку 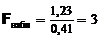 >
> 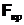 , выборочные дисперсии различаются значимо. Гипотеза о равенстве дисперсий отвергается.
, выборочные дисперсии различаются значимо. Гипотеза о равенстве дисперсий отвергается.
3. Проверка гипотезы о равенстве математических ожиданий двух нормально распределенных случайных величин с равными неизвестными дисперсиями.Пусть нормально распределенные случайные величины x и h независимы и их дисперсии неизвестны. По выборкам малого объема (меньше 30) нельзя получить хорошие оценки дисперсий. Но если предположить, что Dx = Dh, то оказывается, что можно построить критерий Стьюдента для сравнения математических ожиданий. (Если нет уверенности, что дисперсии одинаковы, то, прежде чем сравнивать математические ожидания, следует с помощью критерия Фишера предварительно проверить гипотезу о равенстве дисперсий.)
Обозначим Dx = Dh = s2, Mx = a, Mh = b. Пусть получены выборки 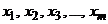 и
и 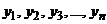 значений соответственно x и h,
значений соответственно x и h, 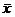 и
и 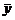 – определяемые этими выборками эмпирические математические ожидания,
– определяемые этими выборками эмпирические математические ожидания, 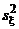 и
и 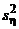 – исправленные эмпирические дисперсии. Так как случайные величины x и h независимы, то
– исправленные эмпирические дисперсии. Так как случайные величины x и h независимы, то 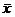 и
и 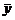 также являются независимыми случайными величинами и притом распределенными по нормальному закону. Отсюда следует, что разность
также являются независимыми случайными величинами и притом распределенными по нормальному закону. Отсюда следует, что разность 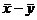 распределена по нормальному закону. При этом имеем
распределена по нормальному закону. При этом имеем 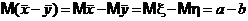 ,
, 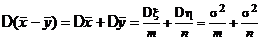 , поэтому случайная величина
, поэтому случайная величина 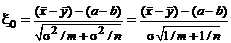 распределена по нормальному закону, причем Mx0 = 0, Dx0 = 1.
распределена по нормальному закону, причем Mx0 = 0, Dx0 = 1.
Из независимости x и h следует независимость случайных величин 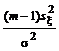 и
и 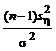 , которые распределены по закону c2 со степенями свободы соответственно m – 1 и n – 1 (см. § 2, п. 3 (в)). Следовательно, случайная величина
, которые распределены по закону c2 со степенями свободы соответственно m – 1 и n – 1 (см. § 2, п. 3 (в)). Следовательно, случайная величина 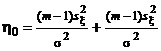 распределена по закону
распределена по закону 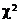 с m + n – 2 степенями свободы (§ 2, п. 3 (б)). Но тогда случайная величина
с m + n – 2 степенями свободы (§ 2, п. 3 (б)). Но тогда случайная величина
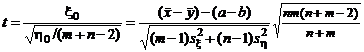 (4)
(4)
распределена по закону Стьюдента с m + n – 2 степенями свободы.
Теперь построим критерий для проверки гипотезы H0: Mx = Mh, т. е. a = b.
Если эта гипотеза верна, то (4) приводится к равенству
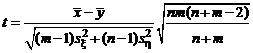 . (5)
. (5)
Случайная величина (5) и является критерием для проверки гипотезы H0.
Случай 1: альтернативная гипотеза a ¹ b. В этом случае строится двусторонняя критическая область такая, чтобы вероятность попадания значения t в эту область в случае справедливости основной гипотезы была равна принятому уровню значимости a.
Поскольку плотность вероятностей распределения Стьюдента – четная функция (см. § 2, п. 3), критические точки симметричны относительно нуля. Поэтому достаточно найти правую критическую точку. Ее находят по таблице критических точек распределения Стьюдента по уровню значимости a / 2 и k = m + n – 2 ( 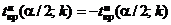 ).
).
Если 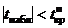 , то основную гипотезу принимают.
, то основную гипотезу принимают.
Если 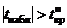 , то основную гипотезу отвергают.
, то основную гипотезу отвергают.
Случай 2: альтернативная гипотеза a > b. Строится правосторонняя критическая область. Единственную критическую точку находят по уровню значимости a и числу степеней свободы n + m – 2 в таблице критических точек распределения Стьюдента: 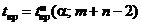 .
.
Если 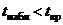 , то основная гипотеза принимается.
, то основная гипотеза принимается.
Если 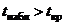 , то основную гипотезу отвергают.
, то основную гипотезу отвергают.
Случай 3: альтернативная гипотеза a < b. В этом случае строится левосторонняя критическая область. Критическая точка 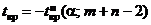 .
.
Если 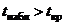 , то основная гипотеза принимается.
, то основная гипотеза принимается.
Если 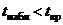 , то основную гипотезу отвергают.
, то основную гипотезу отвергают.
Пример. В ряде экспериментов исследовалось влияние CaO как активатора расширения ангидритовых растворов. Было изготовлено две серии пробных образцов по 6 штук каждая. Серия 0 (нулевая проба) не содержала CaO; серия 1 содержала 1% CaO. По результатам исследований получено: 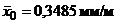 ;
; 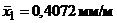 ;
; 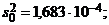
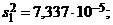
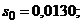
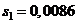 , т. е. имеются точечные оценки параметров двух случайных величин: x0 – расширения раствора, не содержащего CaO, и x1 – расширения раствора, содержащего CaO.
, т. е. имеются точечные оценки параметров двух случайных величин: x0 – расширения раствора, не содержащего CaO, и x1 – расширения раствора, содержащего CaO.
Выясним, значимо ли различие между обоими средними. Для этого проверим гипотезу Mx0 = Mx1 при уровне значимости a = 0,05 и альтернативной гипотезе Mx0 ¹ Mx1.
Так как обе выборки имеют малый объем, то сначала нужно проверить гипотезу о равенстве их дисперсий. В этом случае воспользуемся односторонним критерием, так что конкурирующая гипотеза будет иметь вид: Dx > Dh. По таблице критических точек распределения Фишера по уровню значимости a = 0,05 и числам степеней свободы 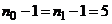 находим
находим 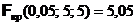 . Так как
. Так как 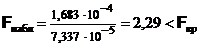 , то исправленные выборочные дисперсии отличаются незначимо. Далее вычисляем
, то исправленные выборочные дисперсии отличаются незначимо. Далее вычисляем 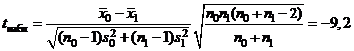 и по таблице критических точек распределения Стьюдента по уровню значимости a / 2 = 0,025 и числу степеней свободы
и по таблице критических точек распределения Стьюдента по уровню значимости a / 2 = 0,025 и числу степеней свободы 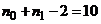 получаем
получаем 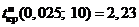 . Так как
. Так как 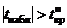 , то основная гипотеза отвергается, другими словами, различие между средними значимо. Таким образом, влияние CaO как активатора расширения ангидритовых растворов существенно.
, то основная гипотеза отвергается, другими словами, различие между средними значимо. Таким образом, влияние CaO как активатора расширения ангидритовых растворов существенно.
4. Эмпирические и теоретические кратности.Пусть имеются основания предполагать, что случайная величина x распределена по некоторому определенному закону. Это предположение можно проверить, сравнивая эмпирические и теоретические кратности. Рассмотрим
Случай 1: предполагаемое распределение дискретно. Пусть в результате n испытаний случайная величина x приняла nj раз значение zj ( j = 1, 2, ..., m; n1 + n2 + ... + + nm = n). Найдем вероятности pj значений zj, считая, что x имеет предполагаемое распределение, и положим 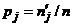 ( j = 1, 2, ..., m). Числа
( j = 1, 2, ..., m). Числа 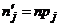 назовем теоретическими кратностями значений zj в выборке объема n. Сравнение теоретических кратностей
назовем теоретическими кратностями значений zj в выборке объема n. Сравнение теоретических кратностей 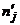 с эмпирическими (наблюдаемыми) кратностями nj дает возможность принять или отвергнуть гипотезу о распределении случайной величины x по предполагаемому закону.
с эмпирическими (наблюдаемыми) кратностями nj дает возможность принять или отвергнуть гипотезу о распределении случайной величины x по предполагаемому закону.
Случай 2: предполагаемое распределение является непрерывным. Тогда вероятности отдельных значений x равны нулю. В этом случае промежуток, содержащий все значения x, разбивают на m непересекающихся промежутков одной той же длины h и вычисляют вероятности pj попадания значения x в j-й промежуток, а затем, как и в случае дискретного распределения, сравнивают теоретические кратности 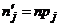 с наблюдаемыми кратностями nj.
с наблюдаемыми кратностями nj.
В частности, если случайная величина x имеет непрерывную плотность вероятностей f, то, обозначая через yj и yj + h концы j-го промежутка, получаем 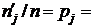
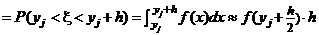 , откуда следует
, откуда следует 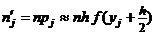 .
.
Близость теоретических кратностей к наблюдаемым подтверждает гипотезу о предполагаемом распределении случайной величины x.
5. Проверка гипотезы о нормальном распределении. Критерий согласия Пирсона. Критерий для проверки гипотезы о предполагаемом законе неизвестного распределения называют критерием согласия. Одним из критериев согласия является критерий 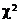 Пирсона, который можно применять для проверки различных гипотез о законе распределения случайной величины. Для построения критерия числовая прямая разбивается на несколько промежутков и устанавливается наблюдаемое и теоретическое число значений случайной величины, попадающее в каждый промежуток. Обычно они различаются. Это различие может быть случайным (незначимым) и объясняется либо малым числом наблюдений, либо способом их группировки, либо другими причинами. Может оказаться, что это различие не случайно (значимо) и объясняется тем, что теоретические кратности вычислены исходя из неверной гипотезы.
Пирсона, который можно применять для проверки различных гипотез о законе распределения случайной величины. Для построения критерия числовая прямая разбивается на несколько промежутков и устанавливается наблюдаемое и теоретическое число значений случайной величины, попадающее в каждый промежуток. Обычно они различаются. Это различие может быть случайным (незначимым) и объясняется либо малым числом наблюдений, либо способом их группировки, либо другими причинами. Может оказаться, что это различие не случайно (значимо) и объясняется тем, что теоретические кратности вычислены исходя из неверной гипотезы.
Здесь будет рассмотрено применение критерия Пирсона для проверки гипотезы о нормальном распределении.
Пусть имеется выборка значений случайной величины x объема n. Отрезок, концами которого являются наименьшая и наибольшая варианты, содержит все числа этой выборки. Разобьем этот отрезок на m частичных промежутков одинаковой длины:
[ y1; y2), [ y2; y3), [ y3; y4), ..., [ ym–1; ym), [ ym; ym+1] (6)
(общие концы двух соседних промежутков отнесены к правому промежутку). Обозначим через nj – число элементов выборки, попавших в j-й промежуток (n1 + n2 + ... + nm = n). Поскольку y1 и ym+1 – наименьшая и наибольшая варианты, то крайние промежутки последовательности (6) можно заменить промежутками (–¥; y2) и [ym; +¥), не меняя значений n1 и nm. Таким образом, мы получаем последовательность промежутков
(–¥; y2), [ y2; y3), [ y3; y4), ..., [ym–1; ym), [ym; +¥), (7)
объединение которых – вся числовая прямая. При этом n1, n2, ..., nm являются количествами чисел имеющейся выборки, попавшими в эти промежутки. Наряду с этими наблюдаемыми количествами можно построить теоретические в предположении, что случайная величина x распределена по нормальному закону. Для этого введем в рассмотрение числа 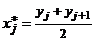 (середины промежутков последовательности (6)). Эти числа называют равноотстоящими вариантами, полученными группировкой выборки. Приписывая им в качестве кратностей числа nj, получим следующий закон распределения
(середины промежутков последовательности (6)). Эти числа называют равноотстоящими вариантами, полученными группировкой выборки. Приписывая им в качестве кратностей числа nj, получим следующий закон распределения
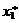 | 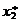 | ... | 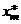 |
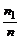 | 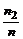 | ... | 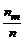 |
Математическим ожиданием и дисперсией этого распределения являются числа
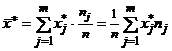 ,
,
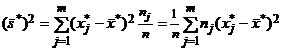 , (8)
, (8)
которые называют выборочными математическим ожиданием и дисперсией, полученными группировкой выборки. При большом n эти числа мало отличаются от 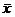 и
и 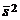 .
.
Рассматривая числа 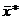 и
и 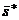 как приближенные значения математического ожидания и квадратичного отклонения случайной величины x и предполагая, что эта случайная величина распределена по нормальному закону, найдем вероятности того, что ее значения попадают в промежутки (7). По формуле (5) из § 2 Введения получаем
как приближенные значения математического ожидания и квадратичного отклонения случайной величины x и предполагая, что эта случайная величина распределена по нормальному закону, найдем вероятности того, что ее значения попадают в промежутки (7). По формуле (5) из § 2 Введения получаем
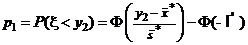 ;
;
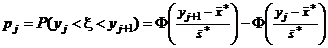
при j = 2, 3, ..., m – 1;
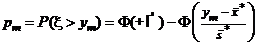 ,
,
где 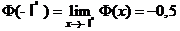 ;
; 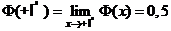 .
.
Теоретические кратности находят по формуле: 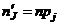 .
.
Рассмотрим теперь случайную величину
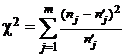 ,
,
которая, как доказал Пирсон, распределена по закону c2 c m – 3 степенями свободы.
Ясно, что, чем меньше различаются числа n¢j и nj, тем меньше наблюдаемое значение этой случайной величины. Поэтому ее можно использовать для проверки гипотезы о нормальном распределении данной случайной величины x.
Построим правостороннюю критическую область, исходя из требования, чтобы вероятность попадания значения критерия в эту область в предположении справедливости основной гипотезы равнялась принятому уровню значимости a. Критическая точка 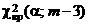 удовлетворяет условию
удовлетворяет условию 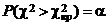 и находится по таблице критических точек распределения c2.
и находится по таблице критических точек распределения c2.
Если 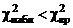 , то основную гипотезу принимают.
, то основную гипотезу принимают.
Если 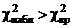 , то нулевую гипотезу отвергают.
, то нулевую гипотезу отвергают.
Пример. Получена выборка значений случайной величины x объема n = 190. Найденные значения распределены по промежуткам следующим образом.
| Промежуток | [4; 6) | [6; 8) | [8; 10) | [10; 12) | [12; 14) |
| Количество | n1 = 15 | n2 = 26 | n3 = 25 | n4 = 30 | n5 = 26 |
| Промежуток | [14; 16) | [16; 18) | [18; 20) | [20; 22] |
| Количество | n6 = 14 | n7 = 16 | n8 = 18 | n9 = 20 |
Проверим гипотезу о нормальном распределении x.
Находим равноотстоящие варианты:
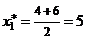 ,
, 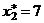 ,
, 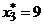 ,
, 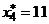 ,
, 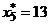 ,
, 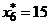 ,
, 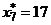 ,
, 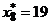 ,
, 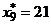 .
.
По формулам (8) получаем 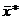 = 12,6,
= 12,6, 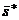 = 4,93.
= 4,93.
Вычисление чисел 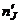 проведено с помощью расчетной таблицы, приведенной на стр. 72.
проведено с помощью расчетной таблицы, приведенной на стр. 72.
| j | yj | 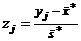 | F(zj) | pj = = F(zj+1) – F(zj) | 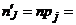 = 190pj = 190pj |
| –¥ | –¥ | –0,5 | 0,0901 | 17,119 | |
| – 1,34 | –0,4099 | 0,0861 | 16,359 | ||
| – 0,93 | –0,3238 | 0,1219 | 23,161 | ||
| – 0,53 | –0,2019 | 0,1541 | 29,279 | ||
| – 0,12 | –0,0478 | 0,1581 | 30,039 | ||
| 0,28 | 0,1103 | 0,1446 | 27,474 | ||
| 0,69 | 0,2549 | 0,1094 | 20,786 | ||
| 1,10 | 0,3643 | 0,0689 | 13,091 | ||
| 1,50 | 0,4332 | 0,0668 | 12,692 | ||
| +¥ | +¥ | 0,5 | |||
| Контроль: | 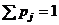 | 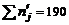 |
Отсюда следует 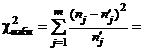 20,41, а по таблице критических точек распределения c2 (табл. 3) находим
20,41, а по таблице критических точек распределения c2 (табл. 3) находим 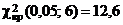 . Так как
. Так как 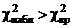 , гипотеза о нормальном распределении x отвергается.
, гипотеза о нормальном распределении x отвергается.
При использовании критерия Пирсона объем выборки должен быть не менее 50 и каждая группа должна содержать не менее пяти чисел выборки.
§ 4. Однофакторный дисперсионный анализ
1. Постановка задачи. Пусть случайные величины x1, x2, ..., xp распределены по нормальному закону и имеют одинаковую и притом неизвестную дисперсию s2, математические ожидания также неизвестны, но могут быть различными. Требуется при заданном уровне значимости проверить гипотезу 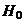 о равенстве всех математических ожиданий: Mx1 = Mx2 = ... = Mxp. Для этого используется метод, основанный на сравнении некоторых дисперсий и поэтому названный дисперсионным анализом.
о равенстве всех математических ожиданий: Mx1 = Mx2 = ... = Mxp. Для этого используется метод, основанный на сравнении некоторых дисперсий и поэтому названный дисперсионным анализом.
На практике дисперсионный анализ применяют, чтобы установить, оказывает ли существенное влияние определенный качественный фактор F, который имеет p уровней F1, F2, ..., Fp на изучаемую величину x, которая под воздействием этих факторов превращается соответственно в x1, x2, ..., xp.
Например, если требуется выяснить, какой вид цемента наиболее эффективен для получения наибольшей прочности бетона, то фактор F есть цемент, а его уровни – виды цемента.
Основная идея дисперсионного анализа состоит в сравнении факторной дисперсии, порождаемой воздействием фактора, с остаточной дисперсией, обусловленной случайными причинами. Если различие между этими дисперсиями значимо, то фактор оказывает существенное влияние на изучаемую величину x.
В этом случае средние наблюдаемых значений (выборочные математические ожидания) на каждом уровне (групповые средние) различаются также значимо. Если уже установлено, что фактор существенно влияет на величину x, и требуется выяснить, какой из уровней оказывает на нее наибольшее воздействие, то дополнительно производят попарно сравнение средних.
Дисперсионный анализ применяют также, чтобы установить однородность нескольких совокупностей, которая понимается в том смысле, что связанные с ними случайные величины при предположенных одинаковых дисперсиях имеют также и одинаковые математические ожидания.
Однородные совокупности можно объединить в одну и тем самым получить о них более полную информацию, а значит, и более надежные выводы.
2. Общая, факторная и остаточная суммы квадратов отклонений. Пусть на количественный признак, значение которого есть нормально распределенная случайная величина, воздействует фактор F, имеющий p постоянных уровней. Пусть проведена группа из q1 испытаний при уровне F1, группа из q2 испытаний при уровне F2, ..., группа из qp испытаний при уровне Fp. Обозначив через xij значение, полученное в i-м испытании при j-м уровне, имеем следующую таблицу результатов.
| i (номер испы- тания) | Уровни фактора | |||
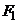 | 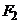 | ... | 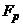 | |
| x11 | x12 | ... | x1p | |
| x21 | x22 | ... | x2p | |
| … | ... | ... | ... | ... |
| q1 | 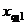 | … | ... | … |
| ... | ... | ... | ... | |
| q2 | 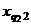 | ... | ... | |
| ... | ... | ... | ||
| qp | ... | 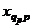 | ||
| Групповая средняя | 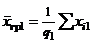 | 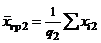 | ... | 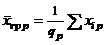 |
Пусть 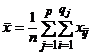 , где
, где 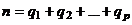 , т. е.
, т. е. 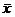 – общее среднее всех xij. Введем в рассмотрение суммы:
– общее среднее всех xij. Введем в рассмотрение суммы:
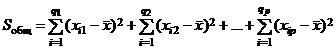 – общая сумма,
– общая сумма,
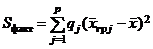 – факторная сумма,
– факторная сумма,
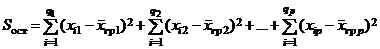 – остаточная сумма.
– остаточная сумма.
Общая сумма является суммой квадратов отклонений наблюдаемых значений от общей средней, факторная сумма есть сумма квадратов отклонений групповых средних от общей средней, остаточная сумма представляет собой сумму квадратов отклонений наблюдаемых значений от своей групповой средней.
Теорема. Выполняется равенство Sобщ = Sфакт + Sост.
Доказательство. Имеем
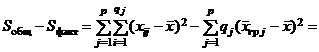
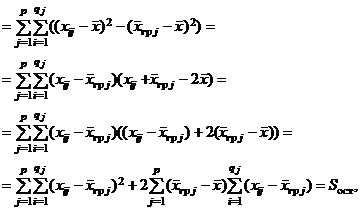
т. к. 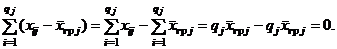
Замечание 1. Если фактор F оказывает существенное влияние на значения количественного признака, то группы наблюдаемых значений, соответствующие различным уровням, заметно отличаются друг от друга. Следовательно, групповые средние больше отклоняются от общей средней, а чем больше это отклонение, тем больше Sфакт. Таким образом, факторная сумма характеризует воздействие фактора на количественный признак. Остаточная сумма Sост суммирует рассеяния наблюдаемых значений относительно групповых средних и, таким образом, является характеристикой воздействия случайных причин. Следовательно, Sобщ = Sфакт + Sост отражает как влияние фактора, так и влияние случайных причин.
Замечание 2. Выражения для общей и факторной сумм можно привести к виду, более удобному для вычислений. Для этого введем обозначения: 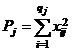 ,
, 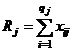 .
.
Используя эти обозначения, получаем
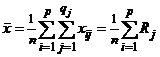 ,
,
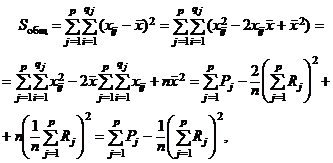
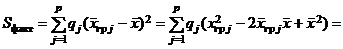
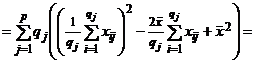
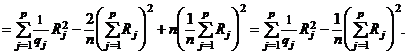
Таким образом, имеют место формулы
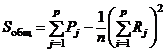 и
и 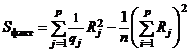 .
.
3. Общая, факторная и остаточная дисперсии. Введем следующие обозначения:
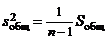 ,
, 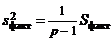 ,
, 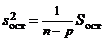 .
.
Эти величины называют соответственно общей, факторной и остаточной дисперсиями. Так как все xij при сделанных в п. 1 предположениях представляют собой независимые случайные величины, распределенные по нормальному закону с дисперсией s2, то 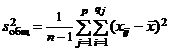 есть несмещенная точечная оценка для s2.
есть несмещенная точечная оценка для s2.
Предположим, что верна гипотеза 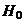 , т. е. Mx1 = Mx2 = = ... = Mxp = a. Тогда
, т. е. Mx1 = Mx2 = = ... = Mxp = a. Тогда 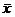 и все групповые средние
и все групповые средние 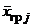 являются несмещенными точечными оценками одного и того же числа а. Поэтому
являются несмещенными точечными оценками одного и того же числа а. Поэтому 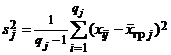 при любом j есть также несмещенная точечная оценка для s2, так что
при любом j есть также несмещенная точечная оценка для s2, так что 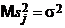 , а следовательно,
, а следовательно, 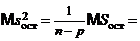
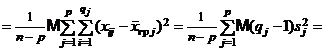
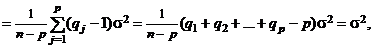
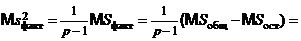
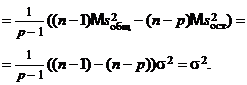
Таким образом, если гипотеза 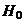 верна, то
верна, то 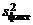 и
и 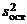 являются несмещенными точечными оценками для дисперсии s2. Можно доказать, что эти оценки являются независимыми случайными величинами. Поэтому при построении критерия для проверки гипотезы
являются несмещенными точечными оценками для дисперсии s2. Можно доказать, что эти оценки являются независимыми случайными величинами. Поэтому при построении критерия для проверки гипотезы 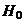 используются именно эти оценки.
используются именно эти оценки.
4. Сравнение нескольких математических ожиданий методом дисперсионного анализа. Пусть случайные величины 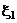 ,
, 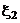 ,...,
,..., 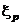 распределены по нормальному закону и имеют одинаковую неизвестную дисперсию s2, математические ожидания также неизвестны, но могут быть различными. Построим критерий для проверки при заданном уровне значимости гипотезы
распределены по нормальному закону и имеют одинаковую неизвестную дисперсию s2, математические ожидания также неизвестны, но могут быть различными. Построим критерий для проверки при заданном уровне значимости гипотезы 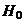 : Mx1 = Mx2 = ... = Mxp .
: Mx1 = Mx2 = ... = Mxp .
Если эта гипотеза верна, то 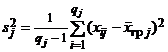 при любом j есть исправленная выборочная дисперсия для xj (см. п. 3), а тогда (§ 2, п. 3 (в)) случайная величина
при любом j есть исправленная выборочная дисперсия для xj (см. п. 3), а тогда (§ 2, п. 3 (в)) случайная величина 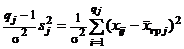 распределена по закону c2 с qj – 1 степенями свободы. Отсюда следует, что случайная величина
распределена по закону c2 с qj – 1 степенями свободы. Отсюда следует, что случайная величина 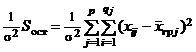 распределена по закону c2 с q1 + q2 + ... + qp – p = n – p степенями свободы. Таким же образом получаем, что случайная величина
распределена по закону c2 с q1 + q2 + ... + qp – p = n – p степенями свободы. Таким же образом получаем, что случайная величина 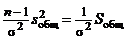 распределена по закону c2 с числом степеней свободы n – 1. Отсюда следует, что разность
распределена по закону c2 с числом степеней свободы n – 1. Отсюда следует, что разность 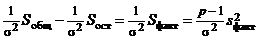 распределена по закону c2 с (n – 1) – (n – p) = p – 1 степенями свободы. Значит, случайная величина
распределена по закону c2 с (n – 1) – (n – p) = p – 1 степенями свободы. Значит, случайная величина
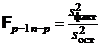
распределена (при условии справедливости гипотезы H0) по закону Фишера со степенями свободы p – 1 и n – p. Эта случайная величина и является критерием для рассматриваемой гипотезы.
Решение задачи сводится к сравнению факторной и остаточной дисперсий по критерию Фишера.
Действительно, если верна гипотеза 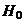 , то факторная и остаточная дисперсии являются несмещенными оценками неизвестной дисперсии (см. п. 3) и, значит, различаются незначимо. Если же гипотеза о равенстве групповых математических ожиданий неверна, то с возрастанием расхождения между групповыми средними возрастает факторная дисперсия, а тогда возрастает и
, то факторная и остаточная дисперсии являются несмещенными оценками неизвестной дисперсии (см. п. 3) и, значит, различаются незначимо. Если же гипотеза о равенстве групповых математических ожиданий неверна, то с возрастанием расхождения между групповыми средними возрастает факторная дисперсия, а тогда возрастает и 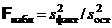 . В конце концов, Fнабл окажется больше Fкр и, значит, гипотеза о равенстве групповых математических ожиданий должна быть отвергнута. Если же окажется Fнабл< Fкр, гипотеза
. В конце концов, Fнабл окажется больше Fкр и, значит, гипотеза о равенстве групповых математических ожиданий должна быть отвергнута. Если же окажется Fнабл< Fкр, гипотеза 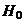 принимается.
принимается.
Если факторная дисперсия окажется меньше остаточной, то отсюда сразу следует справедливость гипотезы о равенстве групповых математических ожиданий, т. е. нет необходимости применять критерий Фишера.
Пример. Пусть произведено 14 испытаний на различных уровнях фактора F: 5 испытаний на уровне F1, 3 испытания на уровне F2, 2 испытания на уровне F3 и 4 испытания на уровне F4. Результаты испытаний представлены следующей таблицей.
| i (номер ис- пытания) | Уровни фактора | |||
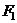 | 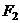 | F3 | F4 | |
| 1,5 | 3,3 | 5,6 | 6,1 | |
| 2,1 | 3,1 | 4,8 | 5,9 | |
| 1,4 | 4,5 | 4,7 | ||
| 2,2 | 4,3 | |||
| 2,4 |
Требуется проверить на уровне значимости a = 0,05 гипотезу о равенстве математических ожиданий нормально распределенных случайных величин x1, x2, x3, x4, возникающих при различных уровнях фактора F. Предполагается, что дисперсии этих случайных величин одинаковы. Обозначим через xij значение, полученное в i-м испытании при j-м уровне фактора, и составим расчетную таблицу.
| i | 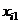 | 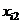 | 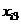 | 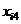 | 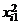 | 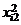 | 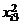 | 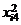 |
| 1,5 | 3,3 | 5,6 | 6,1 | 2,25 | 10,89 | 31,36 | 37,21 | |
| 2,1 | 3,1 | 4,8 | 5,9 | 4,41 | 9,61 | 23,04 | 34,81 | |
| 1,4 | 4,5 | 4,7 | 1,96 | 20,25 | 22,09 | |||
| 2,2 | 4,3 | 4,84 | 18,49 | |||||
| 2,4 | 5,76 | |||||||
| Rj | 9,6 | 10,9 | 10,4 | 21,0 | ||||
| Pj | 19,22 | 40,75 | 54,40 | 112,60 Наши рекомендации
|
