Модуль 3: Линейные операторы
29. Линейные отображения, матрицы, замена базисов, инвариантность ранга.
30.  .
.
31. Изменение матрицы линейного оператора при переходе к новому базису. Ранг и определитель линейного оператора.
32. Алгебра линейных операторов. Изоморфизм 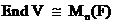 для линейного пространства
для линейного пространства 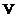 над полем
над полем 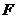 размерности
размерности 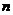 ,
, 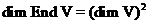 .
.
33. Вид матрицы линейного оператора при наличии инвариантных подпространств.
34. Докажите, что определение характеристического многочлена корректно, то есть не зависит от выбора базиса.
35. Собственные векторы и значения. Число 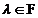 является собственным для линейного оператора
является собственным для линейного оператора 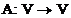 тогда и только тогда, когда
тогда и только тогда, когда 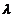 - корень характеристического многочлена.
- корень характеристического многочлена.
36. Любой линейный оператор над полем действительных чисел обладает одномерным или двумерным инвариантным подпространством.
37. Собственные подпространства. Если 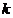 - кратность собственного значения
- кратность собственного значения 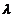 линейного оператора
линейного оператора 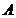 , то
, то 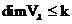 .
.
38. Докажите, что система собственных векторов линейного оператора, отвечающих попарно различным собственным значениям, линейно независима.
39. Критерий существования базиса из собственных векторов линейного оператора.
40. Пусть 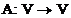 - линейный оператор конечномерного линейного пространства
- линейный оператор конечномерного линейного пространства 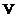 над алгебраически замкнутым полем
над алгебраически замкнутым полем 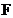 . Тогда существует базис, в котором матрица линейного оператора
. Тогда существует базис, в котором матрица линейного оператора 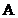 треугольна.
треугольна.
41. Теорема Гамильтона — Кэли.
42. Минимальный многочлен и его свойства.
43. Линейный оператор 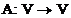 линейного пространства
линейного пространства 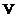 над алгебраически замкнутым полем
над алгебраически замкнутым полем 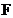 диагонализируем тогда и только тогда, когда его минимальный многочлен не имеет кратных корней.
диагонализируем тогда и только тогда, когда его минимальный многочлен не имеет кратных корней.
44. Жордановы клетки и матрицы, их характеристические и минимальные многочлены. Жорданов базис.
45. Пусть 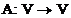 — линейный оператор линейного пространства
— линейный оператор линейного пространства 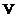 над алгебраически замкнутым полем
над алгебраически замкнутым полем 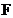 . Тогда в
. Тогда в 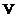 имеется жорданов базис для
имеется жорданов базис для 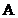 .
.
46. Единственность жордановой нормальной формы.
47. Пусть 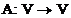 - линейный оператор линейного пространства
- линейный оператор линейного пространства 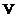 над алгебраически замкнутым полем
над алгебраически замкнутым полем 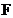 . Тогда
. Тогда 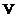 распадается в прямую сумму корневых подпространств, соответствующих всем (различным) собственным значениям оператора
распадается в прямую сумму корневых подпространств, соответствующих всем (различным) собственным значениям оператора 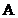 .
.
48. Значение многочлена от жордановой клетки. Вычисление функции от матрицы (без доказательства).
49. Связь между линейным оператором и билинейной функцией в евклидовом пространстве.
50. В евклидовом пространстве любому линейному оператору отвечает сопряженный оператор и притом только один. Связь операции перехода от оператора к сопряженному оператору с операциями сложения и умножения линейных операторов.
51. Матрица симметрического и ортогонального оператора в ортонормированном базисе.
52. Пусть 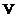 - евклидово пространство,
- евклидово пространство, 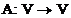 - ортогональный или симметрический линейный оператор линейного пространства
- ортогональный или симметрический линейный оператор линейного пространства 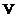 ,
, 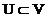 -
- 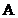 -инвариантное подпространство,
-инвариантное подпространство, 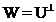 - ортогональное дополнение к
- ортогональное дополнение к 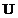 . Тогда
. Тогда 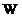 -
- 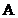 -инвариантное подпространство.
-инвариантное подпространство.
53. Канонический вид симметрического оператора евклидова пространства.
54. Канонический вид ортогонального оператора евклидова пространства.
55. Приведение квадратичной формы к главным осям в евклидовом пространстве.
56. Одновременное приведение пары квадратичных форм к сумме квадратов.
57. Полярное разложение невырожденного линейного оператора евклидова пространства.
58. Приведение эрмитова и унитарного оператора к каноническому виду в унитарном пространстве.
