Определение коэффициентов уравнения регрессии

Будем полагать, что вид уравнения регрессии уже выбран и требуется определить только конкретные численные значения коэффициентов этого уравнения b={bo,.-,b j ,...,b k }. Отметим предварительно, что если выбор вида

уравнения регрессии, как это уже отмечалось, - процесс неформальный и не может быть полностью передан компьютеру, то расчет коэффициентов вы­бранного уравнения регрессии - операция достаточно формальная и ее следу­ет решать с использованием компьютера. Это трудный и утомительный расчет, в котором человек не застрахован от ошибок, а компьютер выполнит его значи­тельно быстрее и качественнее.

Существует два основных подхода к нахождению коэффициентов bj. Вы­бор того или иного из них определяется целями и задачами, стоящими перед исследователем, точностью полученных результатов, их количеством и т.д.

Первый подход - интерполирование. Базируется на удовлетворении ус­ловию, чтобы функция у=(Х,Ь)совпадала с экспериментальными значениями в некоторых точках, выбранных в качестве опорных (основных, главных) у.

4. АНАЛИЗ РЕЗУЛЬТАТОВ ПАССИВНОГО ЭКСПЕРИМЕНТА...

В этом случае для определения к+1 неизвестных значений параметров bj используется система уравнений

f(Xi, bo, ..., bj, ...., b_k) = у, 1<i<n.

(4.4)

В данном случае число независимых уравнений системы равно числу опорных точек, в пределе - п поставленных опытов. С другой стороны, для оп­ределения к+1 коэффициентов необходимо не менее к+1 независимых уравне­ний. Но если число п поставленных опытов и число независимых уравнений равно числу искомых коэффициентов к+1, то решение системы может быть единственно, а следовательно, точно соответствует случайным значениям ис­ходных данных. Таким образом, в предельном случае, когда число коэффици­ентов уравнения регрессии равно

у

-► X

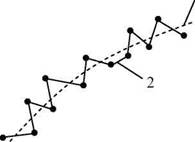
Рис.4.3. Аппроксимация функции с большим (1) и небольшим (2) числом коэффициентов Ь,

числу экспериментальных точек n=k+1, все экспериментальные точки будут совпадать с их рас­четными значениями. Следует заметить, что добиваться такого точного совпадения путем значи­тельного увеличения числа ко­эффициентов уравнения регрес­сии часто просто неразумно, по­скольку экспериментальные ре­зультаты получены с большей или меньшей погрешностью, и

такая функция может просто не отражать действительного характера измене­ния исследуемой величины в силу влияния помех (возмущений) (рис.4.3).

Таким образом, задача в конечном счете сводится к решению системы к+1 уравнений с к+1 неизвестными. Основная сложность такого решения свя­зана с нелинейностью системы, хотя в принципе при использовании компьюте­ра она преодолима.

4. АНАЛИЗ РЕЗУЛЬТАТОВ ПАССИВНОГО ЭКСПЕРИМЕНТА…

При числе опытов п большем, чем к+1 искомых коэффициентов, число независимых уравнений системы избыточно. Избыточность информации можно использовать по-разному.

После определения численных значений к+1 параметров проверяется качество аппроксимации путем сопоставления значений функции и эксперимен­тальных данных в оставшихся, неиспользованных точках. Если обнаруженные между ними расхождения превышают допустимые по условию точности, то процедуру определения коэффициентов bj можно повторить, приняв в качестве опорных (основных) другие точки.

Таким образом, из этих уравнений в разных комбинациях можно соста­вить несколько систем уравнений, каждая из которых в отдельности даст свое решение. Но между собой они будут несовместимыми. Каждое решение будет соответствовать своим значениям коэффициентов bj. Если все их построить на графике, то получим целый пучок аппроксимирующих кривых.

Это открывает при n>k+1 совершенно новые возможности. Во-первых, этот пучок кривых показывает форму и ширину области неопределенности про­веденного эксперимента. Во-вторых, может быть произведено усреднение всех найденных кривых и полученная усредненная кривая будет гораздо точнее и достовернее описывать исследуемое явление, так как она в значительной сте­пени освобождена от случайных погрешностей, приводивших к разбросу от­дельных экспериментальных точек. Поясним суть этого подхода на примере двух методов.

1. Метод избранных точек (рис. 4.4). На основании анализа данных вы­двигают гипотезу о виде (форме) зависимости f(X). Предположим, что она ли­нейная, т.е. статистическая связь - это линейная одномерная регрессия

у = Ьо +Ъ\х. (4.5)

4. АНАЛИЗ РЕЗУЛЬТАТОВ ПАССИВНОГО ЭКСПЕРИМЕНТА...

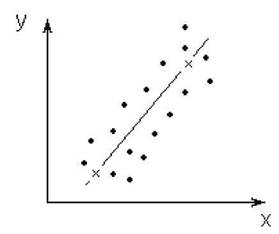Рис.4.4. Метод избранных точек: х-избранные точки

Выбирают две наиболее ха­рактерные, по мнению исследовате­ля, точки, через которые и проходит линия регрессии (рис. 4.4). Задача вычисления коэффициентов Ь₀ и bi в этом случае тривиальна. Если пред­полагается, что уравнение регрессии более высокого порядка, то соответ­ственно увеличивают число избран­ных точек. Недостатки такого подхо­да очевидны, так как избранные точ­ки выбираются субъективно, а по-

давляющая часть экспериментального материала не используется для опреде­ления параметров (коэффициентов) уравнения регрессии, хотя ее можно ис­пользовать в дальнейшем для оценки надежности полученного уравнения.

2. Метод медианных центров. Сущность этого метода поясняет рис.4.5.

у

Уп

У1

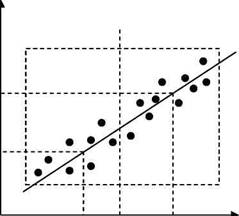
Рис.4.5. Метод медианных точек фициенты регрессии bj. Так, в случае линейной зависимости (4.5) поле делится на две группы. Определяют средние значения xj, yi; xn, yii для каждой из групп, а неизвестные коэффициенты bo, bi определяют из решения системы уравнений:

Обведенное контуром поле точек делят на несколько частей, число которых равно числу определяемых коэффици­ентов уравнения регрессии. В каждой из этих частей находят медианный центр, т.е. пересечение вертикали и горизон­тали слева и справа, выше и ниже кото­рых оказывается равное число точек. Затем через эти медианные центры проводят плавную кривую и из решения системы уравнений определяют коэф-

4. АНАЛИЗ РЕЗУЛЬТАТОВ ПАССИВНОГО ЭКСПЕРИМЕНТА

у, = br,+b,х,;

__ (4.5а)

У п ⁼ ^о + Ь_хх_п.

Если при выборе вида уравнения регрессии число его коэффициентов bj окажется больше числа уравнений (имеющихся результатов измерений) k+1>n, система (4.4) не будет иметь однозначного решения. В этом случае необходимо либо уменьшить число определяемых коэффициентов к+1, либо увеличить число опытов п.

Второй подход - метод наименьших квадратов.Усреднение несовмести­мых решений избыточной системы уравнений п>к+1 может быть преодолено методом наименьших квадратов, который был разработан еще Лежандром и Гауссом. Таким образом, метод наименьших квадратов - это «новинка» почти 200-летней давности. Сегодня, благодаря возможностям компьютеров, этот ме­тод вступил, по существу, в полосу своего «ренессанса».

Определение коэффициентов bj методом наименьших квадратов основа­но на выполнении требования, чтобы сумма квадратов отклонений эксперимен­тальных точек от соответствующих значений уравнения регрессии была мини­мальна. Заметим, что, в принципе, можно оперировать и суммой других четных степеней этих отклонений, но тогда вычисления будут сложнее. Однако руково­дствоваться суммой отклонений нельзя, так как она может оказаться малой при больших отклонениях отрицательного знака.

Математическая запись приведенного выше требования имеет вид

п ₉

Ф(Ъ§,Ъ\,...,Ъ',,...,Ъ\) =^[f(xj,bo,b^,...,bi,...,b]_f) -yj] —> min, (4-6)

i=lbj

где n - число экспериментальных точек в рассматриваемом интервале измене­ния аргумента х.

Необходимым условием минимума функции O(bo,bi...... bj..... b_k) является

выполнение равенства

дФ/дЪ\=0, 0<j<к (4.7)

или

4. АНАЛИЗ РЕЗУЛЬТАТОВ ПАССИВНОГО ЭКСПЕРИМЕНТА…

Д_г„ , _ч -,<9f(x i ) .-,

2^Lt(x i?bo,bj,...,bi,...,b]^) — y{J----- = 0, 0 < j < k. (4-/a)

i=l ^д bJ

После преобразований получим

" ₄9f(x i ) Д df(x\) _Л

2,[f(x i ,bo,bi,...,bi,...,b k)-------------- ZYi----------- ^{= 0}- (4-8)

i=l ^abJ i=l ^abJ

Система уравнений (4.8) содержит столько же уравнений, сколько неиз­вестных коэффициентов bo, b-i,..., bk входит в уравнение регрессии, и называет­ся в математической статистике системой нормальных уравнений.

Поскольку Ф>0 при любых bo, ..., b_k, величина Ф обязательно должна иметь хотя бы один минимум. Поэтому если система нормальных уравнений имеет единственное решение, оно и является минимумом для этой величины.

Расчет регрессионных коэффициентов методом наименьших квадратов можно применять при любых статистических данных, распределенных по лю­бому закону.