Характеристика видов связей между рядами наблюдений

На практике сама необходимость измерений большинства величин вы­зывается тем, что они не остаются постоянными, а изменяются в функции от изменения других величин. В этом случае целью проведения эксперимента яв­ляется установление вида функциональной зависимости j=f(X). Для этого

должны одновременно определяться как значения X, так и соответствующие им значения у, а задачей эксперимента является установление математической модели исследуемой зависимости. Фактически речь идет об установлении свя-зи между двумя рядами наблюдений (измерений).

Определение связи включает в себя указание вида модели и определе­ние ее параметров. В теории экспериментов независимые параметры X=(х-|, ..., х_к) принято называть факторами, а зависимые переменные у - откликами. Ко­ординатное пространство с координатами x-i, х₂, ..., х, ..., х_к называется Фактор­ным пространством. Эксперимент по определению вида функции

у =f(x), (4.1)

где х - скаляр, называется однофакторным. Эксперимент по определению функции вида

у =f(X), (4.1а)

где X=(х-|, х₂, ..., Xi, ..., x_k) - вектор - многофакторным.

Геометрическим представлением функции отклика в факторном про­странстве является поверхность отклика. При однофакторном эксперименте (к=1) поверхность отклика представляет собой линию на плоскости, при двух-факторном (к=2) - поверхность в трехмерном пространстве.

Связи в общем случае являются достаточно многообразными и сложны­ми. Обычно выделяют следующие виды связей.

4. АНАЛИЗ РЕЗУЛЬТАТОВ ПАССИВНОГО ЭКСПЕРИМЕНТА...

Функциональные связи (или зависимости) - это такие связи, когда при изменении величины Xдругая величина у изменяется так, что каждому значе­нию Xj соответствует совершенно определенное (однозначное) значение у (рис.4.1,а). Таким образом, если выбрать все условия эксперимента абсолютно одинаковыми, то, повторяя испытания, получим одну и ту же зависимость, т.е. кривые идеально совпадут для всех испытаний.

К сожалению, такие условия в реальности не встречаются. На практике не удается поддерживать постоянство условий (например, физико-химические свойства шихты при моделировании процессов тепломассопереноса в метал­лургических печах). При этом влияние каждого случайного фактора в отдельно­сти может быть мало, однако в совокупности они существенно могут повлиять на результаты эксперимента. В этом случае говорят о стохастической (вероят­ностной) связи между переменными.

a

б

в

Рис.4.1. Виды связей: а - функциональная связь, все точки лежат на линии; б - связь достаточно тесная, точки группируются возле линии регрессии, но не все они лежат на ней; в - связь слабая

Стохастичность связи состоит в том, что одна случайная переменная у реагирует на изменение другой Xизменением своего закона распределения (см. рис. 4.1, б). Таким образом, зависимая переменная принимает не одно кон­кретное значение, а некоторое из множества значений. Повторяя испытания, мы будем получать другие значения функции отклика, и одному и тому же зна­чению X в различных реализациях будут соответствовать различные значения

4. АНАЛИЗ РЕЗУЛЬТАТОВ ПАССИВНОГО ЭКСПЕРИМЕНТА…

у в интервале [x_min; x_max]- Искомая зависимость у =f(X) может быть найдена лишь в результате совместной обработки полученных значений Xи у.

На рис. 4.1, б - это кривая зависимости, проходящая по центру полосы экспериментальных точек (математическому ожиданию), которые могут и не лежать на искомой кривой у =f(X), а занимают некоторую полосу вокруг нее. Эти отклонения вызваны погрешностями измерений, неполнотой модели и учи­тываемых факторов, случайным характером самих исследуемых процессов и другими причинами.

Анализ стохастических связей приводит к различным постановкам задач статистического исследования зависимостей, которые упрощенно можно клас­сифицировать следующим образом:

1) задачи корреляционного анализа - задачи исследования наличия взаимо­связей между отдельными группами переменных ;

2) задачи регрессионного анализа - задачи, связанные с установлением ана­литических зависимостей между переменным у и одним или несколькими переменными x-i, х₂, ..., Xi, ..., x_k, которые носят количественный характер;

3) задачи дисперсионного анализа - задачи, в которых переменные х-i, х₂, ..., Xi, ..., x_k имеют качественный характер, а исследуется и устанавливается степень их влияния на переменное у.

Стохастические зависимости характеризуются формой, теснотой связи и численными значениями коэффициентов уравнения регрессии.

Форма связи устанавливает вид функциональной зависимости y=f(X) и характеризуется уравнением регрессии. Если уравнение связи линейное, то имеем линейную многомерную регрессию, в этом случае зависимость у от Xописывается линейной зависимостью в k-мерном пространстве:

к

у = Ь₀+^Ь_:х_:, (4.2)

/=1

где bo, ..., bj, ..., b_k - коэффициенты уравнения. Для пояснения существа ис­пользуемых методов ограничимся сначала случаем, когда х - скаляр. В общем

4. АНАЛИЗ РЕЗУЛЬТАТОВ ПАССИВНОГО ЭКСПЕРИМЕНТА…

случае виды функциональных зависимостей в технике достаточно многообраз­ны: показательные у = brjx 1 , логарифмические y = t>olg(x) и т.д.

Заметим, что задача выбора вида функциональной зависимости - задача неформализуемая, так как одна и та же кривая на данном участке примерно с одинаковой точностью может быть описана самыми различными аналитиче­скими выражениями. Отсюда следует важный практический вывод. Даже в наш век компьютеров принятие решения о выборе той или иной математической модели остается за исследователем. Только экспериментатор знает, для чего будет в дальнейшем использоваться эта модель, на основе каких понятий бу­дут интерпретироваться ее параметры.

Крайне желательно при обработке результатов эксперимента вид функ­ции y=f(X) выбирать, исходя из условия ее соответствия физической природе

изучаемых явлений или имеющимся представлениям об особенностях поведе­ния исследуемой величины. К сожалению, такая возможность не всегда имеет­ся, так как эксперименты чаще всего проводятся для исследования недоста­точно или неполно изученных явлений.

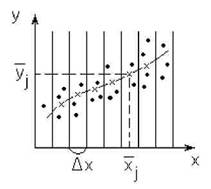При изучении зависимости y=f(x)

от одного фактора при заранее неиз­вестном виде функции отклика для при­ближенного определения вида уравне­ния регрессии полезно предварительно построить эмпирическую линию регрес­сии (рис.4.2). Для этого весь диапазон

изменения х разбивают на равные ин-

Рис.4.2. К построению

тервалы Ах. Все точки, попавшие в дан-

эмпирической линии регрессии

ный интервал Axj, относят к его середи­не ^j . Для этого подсчитывают частные

средние для каждого интервала:

П;

Eyji

у; = ——. (4.3)

^J п;

4. АНАЛИЗ РЕЗУЛЬТАТОВ ПАССИВНОГО ЭКСПЕРИМЕНТА…

к* Здесь nj - число точек в интервале Axj, причем Znj = ^п - ^гД^е к* - число интер-

j=l

валов разбиения; п - объем выборки.

Затем последовательно соединяют точки (х,;у,) отрезками прямой. По­лученная ломаная называется эмпирической линией регрессии. По виду эмпи­рической линии регрессии можно в первом приближении подобрать вид урав­нения регрессии y=f(x).

Под теснотой связи понимается степень близости стохастической зави­симости к функциональной, т.е. показатель тесноты группирования экспери­ментальных данных относительно принятого уравнения модели (см. рис. 4.1,6,в). В дальнейшем уточним это положение.