Вычисление длины дуги плоской кривой

Если кривая у = f(x) на отрезке [a; b] имеет непрерывную производную, то длина дуги этой кривой находится по формуле

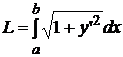(9.11)

При параметрическом задании кривой x = x(t), y = y(t) (функции x(t) и y(t) непрерывно дифференцируемы при изменении t от t₁ до t₂) длина дуги равна

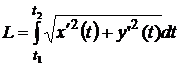. (9.12)

В полярной системе координат длину дуги вычисляют по формуле

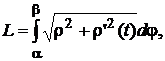(9.13)

где α и β – значения полярного угла, соответствующие концам дуги.

Вычисление объёма тела вращения и его поверхности

Если на кривой у = f(x) непрерывно дифференцируемой на отрезке [a;b] определить значения f(а) и f(b), то можно образовать криволинейную трапецию с вершинами А(а;0), В(а; f(а)), С(b; f(b)) и D(b;0). Вращение этой трапеции вокруг оси абсцисс образует тело, объём и площадь поверхности которого определяются формулами:

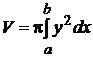(9.14)

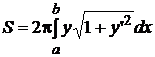
При вращении трапеции, ограниченной кривой х =F(y) (c ≤ y≤ d), вокруг оси ОY объем, полученной фигуры определяется формулой

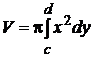. (9.15)

Примеры:

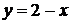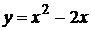1. Вычислить площадь фигуры, ограниченной линиями: . и (рис. 9.4).

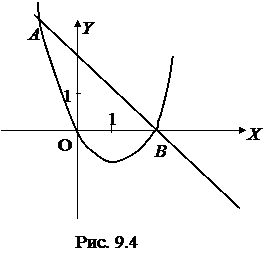
Решение:найдем координаты точек пересечения данных линий, решив систему двух уравнений

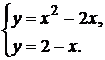
Точки пересечения данных линий: А(-1;3) и В(2;0).

Фигура сверху ограничена кривой 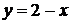, снизу 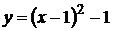. Применяя формулу (9.8), получим

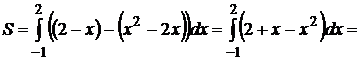
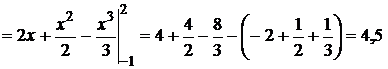(ед.)².

Ответ: S = 4,5 (ед.)².

2. Вычислить площадь фигуры, ограниченной линиями: 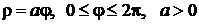(рис.9.5).

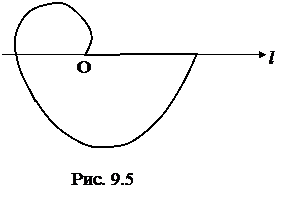Решение:площадь данной фигуры (рис. 9.5) вычислим по формуле (9.10)

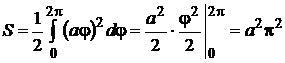(ед)².

3. Вычислить объем тела, образованного вращением вокруг оси ОХ плоской фигуры, ограниченной линиями

.

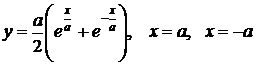Решение:применяя формулу (9.14), получим

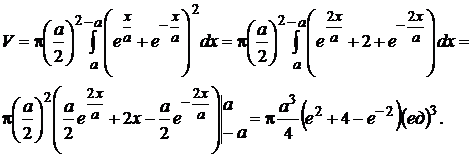
4. Найти длину дуги кривой:

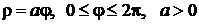(рис.9.5).

Решение: так как 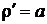, то применяя формулу (9.13), получим

.

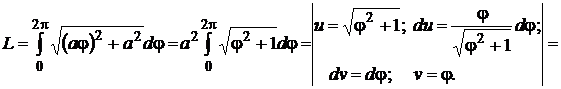
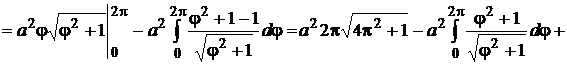
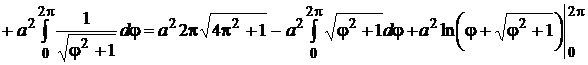Таким образом, получили уравнение относительно неизвестного интеграла

.

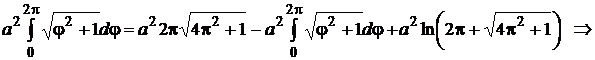
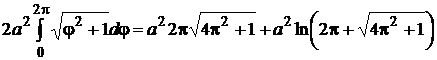Ответ: 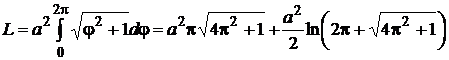(ед).

Вычисление работы силы

Работа, совершаемая переменной силой F = f(x) в направлении оси абсцисс на отрезке [a;b] вычисляется по формуле

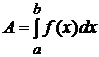. (9.16)

Задания для самостоятельной работы

1. Применяя формулы (9.8)–(9.10), вычислить площади плоских фигур:

1.1. 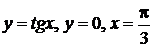; 1.2. 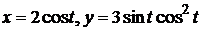; 1.3. .

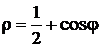2. Найти длины дуг кривых, используя формулы (9.11) –(9.13):

2.1. 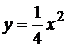, 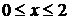; 2.2.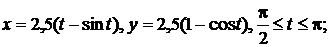

2.3. .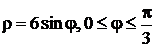

3. Вычислить объем тела, образованного вращением вокруг оси ОY плоской фигуры, ограниченной линиями .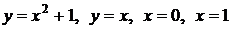

4. Вычислить объем тела, образованного вращением вокруг оси ОХ плоской фигуры, ограниченной линиями .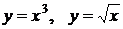

Вопросы для самоподготовки

1. Определение определенного интеграла.

2. Условие интегрируемости функции

3. Свойства определенного интеграла.

4. Геометрический и физический смысл определенного интеграла.

5. Вычисление определенного интеграла.

6. формула Ньютона-Лейбница.

7. Замена переменной в определенном интеграле.

8. метод интегрирования по частям в определенном интеграле.

9. Несобственные интегралы с бесконечными пределами.

10.Несобственные интегралы от разрывных функций.

11.Признаки сходимости несобственных интегралов.

12.Вычисление площади плоской фигуры.

13.Вычисление длины дуги плоской кривой.

14.Вычисление объема тела, полученного вращением плоской фигуры вокруг координатных осей.

10. Функции нескольких переменных

При рассмотрении функций нескольких переменных ограничимся подробным описанием функций двух и трех переменных, т.к. все полученные результаты будут справедливы для функций произвольного числа переменных.

10.1. Множества на плоскости и в пространстве

Понятие множество является одним из основных понятий математики. Под множеством понимают совокупность некоторых объектов, объединенных по какому-либо признаку. Объекты, из которых состоит множество, называются его элементами.

Рассмотрим множество точек плоскости R² и пространства R³. Расстояние между точками плоскости М₁(х₁, х₂) и М₂(у₁, у₂) определяется равенством

,

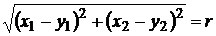а расстояние между точками М₃(х₁, х₂, х₃) и М₄ (у₁, у₂, у₃) пространства R³ определяется равенством

.

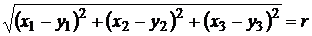Определение. ε-окрестностью точки М₀(х₀, у₀) (рис.10.1) называется совокупность всех точек (х; у), которые удовлетворяют условию

.

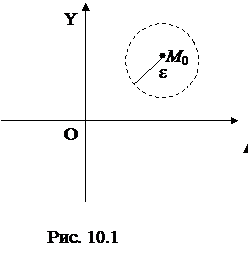
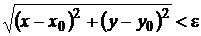Определение. Точка М₀ называется внутренней точкой множества D, если она принадлежит этому множеству вместе со своей некоторой ε-окрестностью.

Определение. Множество D называется открытым, если каждая его точка - внутренняя.

Определение. Точки называются граничными, если среди точек ее окрестности есть как точки, принадлежащие множеству D, так и точки, не принадлежащие множеству D.

Определение. Множество, содержащее внутренние точки и точки границы, называется замкнутым.

Определение. Множество D называется ограниченным, если существует круг конечного радиуса, целиком накрывающий данное множество.

Определение. Множество D называется связным, если для любой пары его точек А и В существует непрерывный путь, целиком принадлежащий множеству D.

Определение. Открытое и связное множество называется областью.

10.2. Понятие функции нескольких переменных

Определение. Пусть D – некоторое множество пар действительных чисел и пусть каждой паре (х; у) из D поставлено в соответствие число z. Тогда говорят, что на множестве D задана функция двух переменных z = f(x,y). Переменные х, у называются независимыми (или аргументами), z – зависимой переменной или функцией, а f(x,y) есть значение функции в точке (х, у).

Геометрически функция z = f(x,y) представляет собой поверхность F изображенную на рис.10.2.

Определение. Областью определения функции z называется совокупность пар (х, у), при которых функция z определена.

Определение. Если паре чисел (х, у) соответствует одно значение z, то функция называется однозначной, а если более одного, то – многозначной.

Пример:

Найти область определения функции .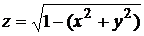

Решение: так как корень четной степени существует только для положительных или равных нулю чисел, то

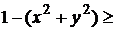0 отсюда следует, что 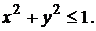Этому неравенству удовлетворяет множество точек, лежащих внутри и на границе круга, радиуса один, с центром в начале координат.

10.3. Предел функции двух переменных

Определение. Число А называется пределом функции f(x,y) при стремлении точки М(х,у) к точке М₀(х₀,у₀), если для каждого числа e > 0 найдется такое число δ >0, что для любой точки М(х, у) из δ-окрестности точки М₀, для которых верно условие

,

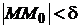выполняется условие .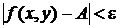

Записывают: .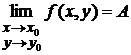

Предел функции f(x, y) не зависит от способа стремления точки М(х,у) к точке М₀(х₀,у₀).

10.4. Непрерывность функции двух переменных

Определение. Функция z = f(x,y) называется непрерывной в точке М₀(х₀,у₀), если она удовлетворяет условиям:

а) функции f(x,y) определена в точке М₀(х₀;,у₀);

б) существует предел функции в точке М₀, равный значению функции f(x,y) в этой точке

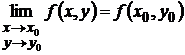, (10.1)

причем точка М(х, у) стремится к точке М₀(х₀,у₀) произвольным образом.

Если в какой – либо точке условие (10.1) не выполняется, то эта точка называется точкой разрыва функции f(x,y). Это может быть в следующих случаях:

1) функция z = f(x,y) не определена в точке М₀(х₀,у₀).

2) не существует предел .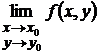

3) этот предел существует, но он не равен f(x₀,y₀).

Определение. Функция z = f(x,y) непрерывная в каждой точке области D называется непрерывной и данной области.

Свойства непрерывных функций

Свойство. Если функция f(x,y) определена и непрерывна в замкнутой и ограниченной области D, то в этой области найдется, по крайней мере, одна точка N(x₀, y₀), такая, что для остальных точек области верно неравенство

f(x₀,y₀) ³ f(x,y),

а также точка N₁(x₀₁,y₀₁), такая, что для всех остальных точек верно неравенство

f(x₀₁,y₀₁) £ f(x,y).

Тогда f(x₀,y₀) =М, где M – наибольшее значение, а f(x₀₁,y₀₁) = m – наименьшее значение функции f(x,y) в области D.

Свойство. Непрерывная функция в замкнутой и ограниченной области D достигает на нем своего наибольшего и наименьшего значения.

Свойство. Если функция f(x,y) определена и непрерывна в замкнутой ограниченной области D, а M и m – соответственно наибольшее и наименьшее значения функции в этой области, то для любой точки m Î [m, M] существует точка N₀(x₀,y₀) такая, что f(x₀,y₀) = m .

То есть, непрерывная функция принимает в области D все промежуточные значения между M и m. Следствием этого свойства может служить заключение, что если числа M и m разных знаков, то в области D функция, по крайней мере, один раз обращается в ноль.

Свойство. Функция f(x,y), непрерывная в замкнутой ограниченной области D, ограничена в этой области, то есть существует такое число К>0, что для всех точек области верно неравенство .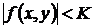

Свойство. Если функция f(x,y) определена и непрерывна в замкнутой ограниченной области D, то она равномерно непрерывна в этой области, то есть для любого положительного числа e существует такое число D > 0, что для любых двух точек (х₁,y₁) и (х₂,у₂) области, для которых

,

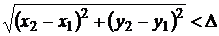выполняется неравенство

.

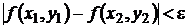Приведенные выше свойства аналогичны свойствам функций одной переменной, непрерывных на отрезке.

10.5. Производные и дифференциалы функций нескольких переменных.

Определение. Пусть в некоторой области задана функция z = f(x,y). Возьмем произвольную точку М(х;у) и зададим приращение Dх переменной х. Тогда величина D_х z = f(x + Dx,y) – f(x,y) называется частным приращением функции по х.

Тогда

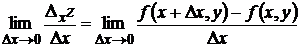
называется частной производной функции z = f(x,y) по х и обозначается

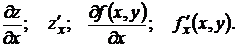
Аналогично определяется частная производная функции z по переменной у.

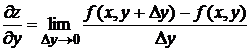
Геометрическим смыслом частной производной 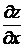является тангенс угла наклона касательной, проведенной в точке N₀(x₀, y₀, z₀) к сечению поверхности z = f(x,y) плоскостью у = у₀.

Примеры:

Найти частные производные функций

1. .

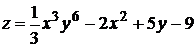Решение: применяя правило дифференцирования суммы и формулу , получим

, .

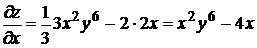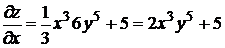2. .

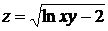Решение: так как 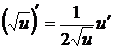, то

.

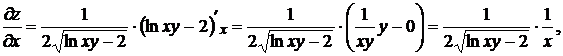
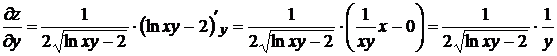3.z = arctg .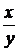

Решение: так как (arctg u)′ = 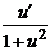, то

, .

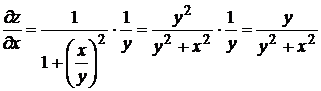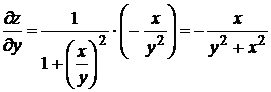3. .

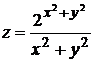Решение: применяя правило дифференцирования дроби:

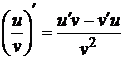, получим

,

.

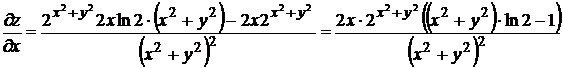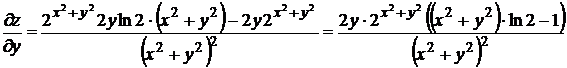Дифференцирование сложной функции

Пусть задана функция z = f(u,v), имеющая непрерывные частные производные z′_u и z′_v. Ее полное приращение можно представить в виде

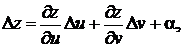(10.2)

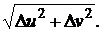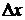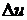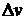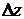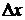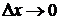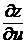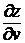где α – бесконечно малая более высокого порядка малости, чем Пусть функции u и v являются дифференцируемыми функциями переменной x. Тогда z = f(u(x),v(x)) = F(х) – сложная функция переменной x. Придадим аргументу x приращение , тогда u и v получат соответственно приращения и , через которые выражается по формуле (10.2). Разделим это равенство на и перейдем к пределу при , учитывая, что и не зависят от :

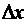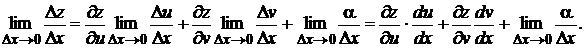
Покажем, что 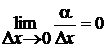. Представим 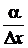в виде

.

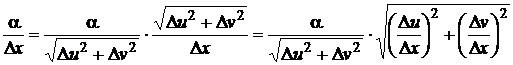Первый множитель стремиться к 0, согласно определению, а второй стремится к определенному числу 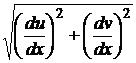, окончательно получим

.

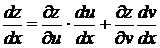Пусть теперь z является сложной функцией двух независимых переменных x и y, то есть z = f(u,v), где u(x,y), v(x,y). Тогда частные производные функции z по независимым переменным x и y имеют вид:

,

.

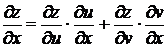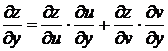Итак, частная производная сложной функции равна сумме произведений частных производных заданной функции по промежуточным аргументам (u,v) на частные производные этих аргументов(u,v) по соответствующей независимой переменной ( x или y).

Примеры:

1. Найти производную 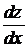для функции z = u² + v² , если 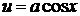, , 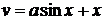где a – постоянная величина.

Решение: так как 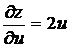, , 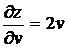, , 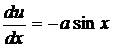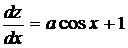то получаем

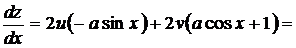
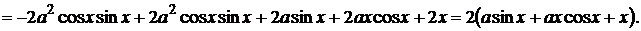2. Найти частные производные функции z = 2 u³ v, если u= x – y, v=x∙y.

Решение: так как 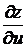= 6u²v, 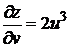, 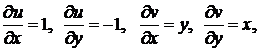получаем

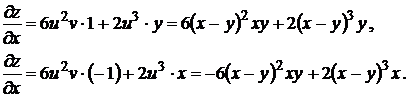
Дифференцирование неявной функции

Определение. Функция называется неявной, если она задается уравнением неразрешенным относительно зависимой переменной

F(x,y,z)=0.

Теорема: пусть функция F(x,y,z) непрерывно дифференцируема в некоторой окрестности точки (x₀, y_0, z₀). Если: F(x₀,y₀, z₀)=0, а F′(x₀,y₀, z₀) 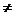0, то существует окрестность точки (x₀, y₀, z₀), в которой уравнение F(x,y,z) = 0 однозначно разрешимо относительно z, то есть существует окрестность точки (x₀, y₀) и единственная непрерывная дифференцируемая функция z = f(x,y), такая, что

F(x,y,f(x,y)) 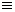0 и z₀=f(x₀,y₀).

Частные производные функции z=f(x,y), в этом случае, вычисляются по формулам

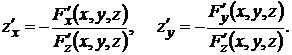(10.3)

Пример:

Неявная функция задана уравнением x³y + ln zy – xz = 0. Найти частные производные 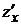и .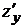

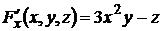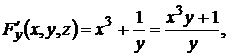
Решение: применяя формулу (10.3), получим , 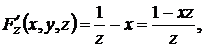следовательно

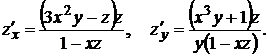
полный дифференциал

Определение. Пусть дана точка М(х,у) и М₁(х+Dx, y + Dy) – близкая точка, отвечающая приращениям Dx и Dy. полным приращением функции f(x, y) называется выражение

Dz = f(x + Dx, y + Dy) – f(x, y).

Определение. функция z = f(x, y) называется дифференцируемой в точке М, если в некоторой окрестности этой точки полное приращение функции можно представить в виде

Dz = АDx + ВDy + ε, (10.4)

где А и В –некоторые постоянные; Dx = x – x₀, Dy = y – y₀; ε – бесконечно малая величина более высокого порядка по сравнению с расстоянием 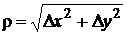между точками М и М₁ (то есть 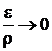при ).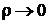

Выясним смысл коэффициентов А и В в равенстве (10.4).

Теорема: (необходимое условие дифференцируемости). Если функция z = f(x, y) дифференцируема в точке М(х,у), то в этой точке существуют частные производные по всем переменным, причем

.

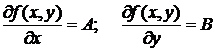Таким образом, из дифференцируемости функции f(x, y) в точке М следует, существование в этой точке всех её производных и для полного приращения имеет место представление

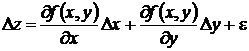. (10.5)

Из равенств (10.4) и (10.5) вытекает, что если Dх ® 0 и Dу ® 0, то и Dz® 0, то есть дифференцируемая в точке М функция f(x, y) непрерывна в этой точке.

Однако из непрерывности функции многих переменных в точке М, а также из существования её частных производных в этой точке еще не следует дифференцируемость функции.

Теорема: (достаточные условия дифференцируемости функции). Если функция z = f(x, y) в окрестности точки М(х,у) имеет непрерывные частные производные 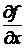и 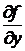, то она дифференцируема в точке М. (Доказать теорему предлагается самостоятельно).

Определение. Полным дифференциалом функции z = f(x, y) называется главная линейная относительно Dх и Dу часть приращения функции Dz в точке (х, у).

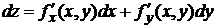. (10.6)

Для функции произвольного числа переменных:

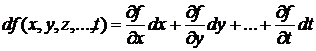. (10.7)

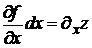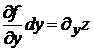Соотношения и называются частными дифференциалами.

Примеры:

1. Найти полный дифференциал функции .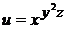

Решение: из равенства (10.7) следует, что

.

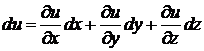Найдем частные производные

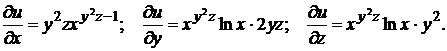
Тогда .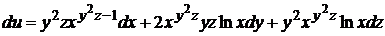

2. Найти полный дифференциал функции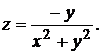

Решение: применяя равенство (10.6), получим

.

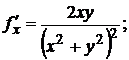
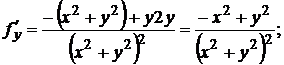
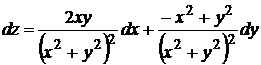10.6. Касательная плоскость и нормаль к поверхности.

Определение. Пусть F некоторая поверхность и М₀(х₀, у₀) – какая-либо точка на ней. Касательной плоскостью Р к поверхности F в точке М₀ называется плоскость ,в которой расположены касательные к всевозможным кривым, проведенным на поверхности F через точку М₀ (рис.10.1).

Определение. Нормалью n к поверхности F в точке М₀ называется прямая, проходящая через точку М₀ перпендикулярно касательной плоскости к этой поверхности в точке М₀ (рис.10.2).

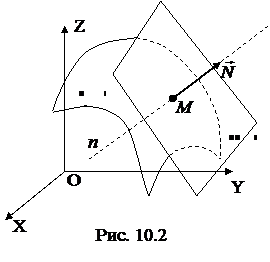В какой – либо точке поверхность имеет, либо только одну касательную плоскость, либо не имеет ее вовсе.

Если поверхность задана уравнением z = f(x, y), где f(x, y) – функция, дифференцируемая в точке М₀(х₀, у₀), то касательная плоскость в точке М₀(x₀,y₀,z₀) (z₀ = f(х₀, у₀)) существует и имеет уравнение:

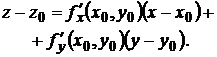(10.8)

Уравнение нормали к поверхности в этой точке:

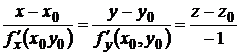. (10.9)

Если поверхность задана уравнением, не разрешенным относительно z: F(х,y, z) = 0, то уравнение касательной плоскости имеет вид

,

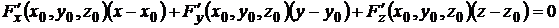а уравнение нормали −

.

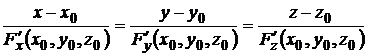Геометрический смысл полного дифференциала

Геометрическим смыслом полного дифференциала функции двух переменных f(x, y) в точке М₀(х₀, у₀) является приращение аппликаты (координаты z) касательной плоскости к поверхности при переходе от точки (х₀, у₀) к точке (х₀+Dх, у₀+Dу).

Пример:

Найти уравнения касательной плоскости и нормали к поверхности

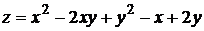в точке М(1, 1, 1).

Решение: для применения формул (10.8) и (10.9) найдем частные производные данной функции в заданной точке

. .

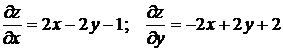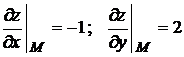Уравнение касательной плоскости:

.

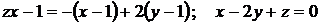Уравнение нормали:

.

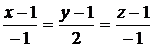10.7. Приближенные вычисления с помощью полного дифференциала

Пусть функция f(x, y) дифференцируема в точке (х, у). Найдем полное приращение этой функции:

Dz = f(x + Dx, y + Dy) – f(x, y),

f(x + Dx, y + Dy) = Dz + f(x, y). (10.10)

Из формул (10.5) и (10.6) следует, что

.

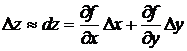Подставим эту формулу выражение (10.10), то получим приближенную формулу:

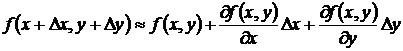. (10.11)

Пример:

Вычислить приближенно значение 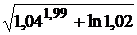, исходя из значения функции 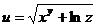при x = 1, y = 2, z = 1.

Решение: из заданного выражения определим

Dx = 1,04 – 1 = 0,04, Dy = 1,99 – 2 = – 0,01, Dz = 1,02 – 1 = 0,02.

Найдем значение функции u(1, 2, 1) = .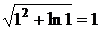

Для функции трех переменных формула (10.11) примет вид

.

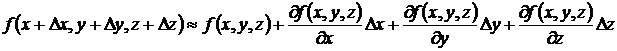Находим частные производные и вычисляем их в точке М(1,2,1):

, ,

.

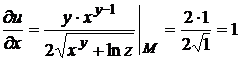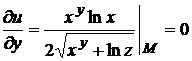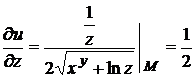Полный дифференциал функции u равен:

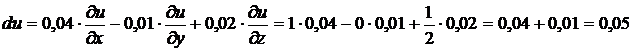
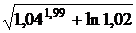
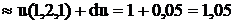
Точное значение этого выражения: 1,049275225687319176.

10.8. Частные производные и дифференциалы высших порядков

Если функция f(x, y) определена в некоторой области D, то ее частные производные 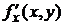и 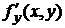тоже будут определены в той же области или ее части.

Будем называть эти производные частными производными первого порядка. Производные этих функций будут частными производными второго порядка.

.

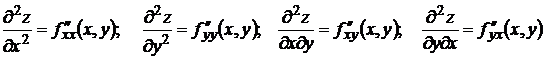Продолжая дифференцировать полученные равенства, получим частные производные более высоких порядков.

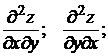
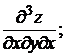
Определение. Частные производные вида 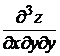и так далее называются смешанными производными.

Теорема: Если функция f(x, y) и ее частные производные 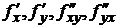определены и непрерывны в точке М(x, y) и ее окрестности, то верно соотношение

.

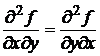То есть частные производные высших порядков не зависят от порядка дифференцирования.

Аналогично определяются дифференциалы высших порядков.

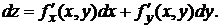
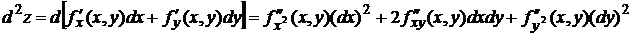
Пример: Найти вторые частные производные функции z = x² + y cos y.

Решение: ,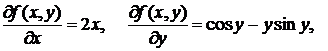

.

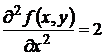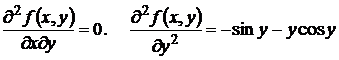10.9. Экстремум функции нескольких переменных.

Определение. Если для функции z = f(x, y), определенной в области D, в некоторой окрестности точки М₀(х₀, у₀) 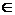D выполняется неравенство

,

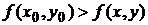то точка М₀ называется точкой максимума.

Определение. Если для функции z = f(x, y), определенной в области D, в некоторой окрестности точки М₀(х₀, у₀) 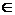D выполняется неравенство

,

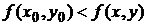то точка М₀ называется точкой минимума.

Теорема: (необходимые условия экстремума). Если функция f(x,y) в точке (х₀, у₀) имеет экстремум, то в этой точке либо частные производные первого порядка равны нулю 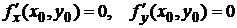, либо хотя бы одна из них не существует.

Эту точку (х₀, у₀) будем называть критической точкой.

Теорема: (достаточные условия экстремума).

Пусть в окрестности критической точки (х₀, у₀) функция f(x, y) имеет непрерывные частные производные до второго порядка включительно. Рассмотрим выражение:

.

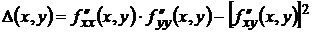1) Если Δ(x₀, y₀) > 0, то в точке (х₀, у₀) функция f(x, y) имеет экстремум, если 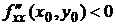– максимум, если 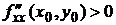– минимум.

2) Если Δ(x₀, y₀) < 0, то в точке (x₀, y₀) функция f(x, y) не имеет экстремума

В случае, если Δ = 0, вывод о наличии экстремума сделать нельзя.

10.10. Условный экстремум.

Условный экстремум находится, когда переменные х и у, входящие в функцию u = f(x, y), не являются независимыми, то есть существует некоторое соотношение j(х, у) = 0, которое называется уравнением связи.

Тогда из переменных х и у только одна будет независимой, так как другая может быть выражена через нее из уравнения связи.

Тогда u = f(x, y(x))

.

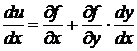В точках экстремума 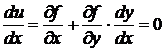. (10.12)

Кроме того:

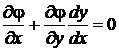. (10.13)

Умножим равенство (10.13) на число l и сложим с равенством (10.12).

.

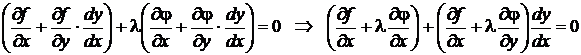Для выполнения этого условия во всех точках найдем неопределенный коэффициент l так, чтобы выполнялась система трех уравнений:

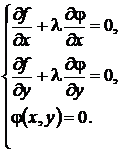(10.14)

Полученная система уравнений является необходимыми условиями условного экстремума. Однако это условие не является достаточным. Поэтому при нахождении критических точек требуется их дополнительное исследование на экстремум.

Выражение u = f(x, y) + lj(x, y) называется функцией Лагранжа.

Пример:

Найти экстремум функции f(x, y) = xy, если уравнение связи:

2x + 3y – 5 = 0.

Решение: функция Лагранжа в данном случае имеет вид

.

; ;

; ; .

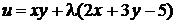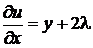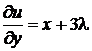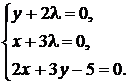
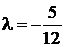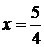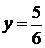Таким образом, функция имеет экстремум в точке .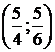

Использование функции Лагранжа для нахождения точек экстремума функции называется также методом множителей Лагранжа.

Все рассуждения относительно условного экстремума, рассмотренные для функции двух переменных, могут быть распространены на функции большего числа переменных.

10.11. Производная по направлению

Определение. Если указан закон, по которому каждой точке М некоторой области V пространства поставлено в соответствие число u(М), то область V называется скалярным полем. Если выбрана некоторая декартова система координат, то задание скалярного поля эквивалентно заданию функции трех переменных

u(М) = u(x; y; z)

в пространстве или заданию функции двух переменных

u(М) = u(x; y)

на плоскости: в этом случае поле u(М) называется плоским полем.

Определение. Производной функции u(x; y; z) по направлению вектора 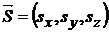в точке М(x; y; z) называется предел

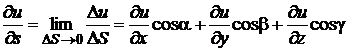= , (10.15)

где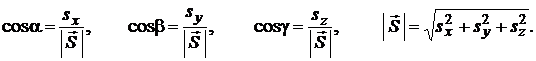

Производная поля u(М) по направлению кривой L в точке М(x; y; z) совпадает с производной по направлению касательной

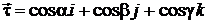
к L в данной точке.

Абсолютная величина 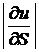определяет скорость изменения скалярного поля в точке М(x; y; z) в направлении вектора 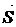, а знак – характер его изменения (плюс – возрастания, минус – убывания).

Пример:

Вычислить производную функции z = x² + y²x в точке А(1; 2) по направлению вектора 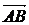, если В (3; 0).

Решение: определим координаты вектора 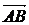и его длину:

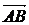= (3–1; 0–2) = (2; –2) = 2 ;

= .

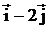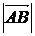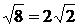Находим частные производные функции z и их значения в точке А:

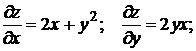
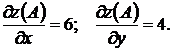
Вычислим направляющие косинусы вектора :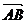

.

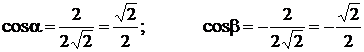За вектор 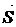принимается произвольный вектор, направленный параллельно заданному вектору 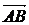, то есть вектору, определяющему направление дифференцирования.

Применяя формулу (10.15), получаем значение производной заданной функции по направлению вектора :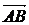

.

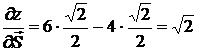Так как производная по направлению вектора 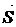имеет знак плюс, то скалярное поле в данном направлении возрастает.

Градиент.

Определение. Градиентом скалярного поля u(М) = u(x; y; z) есть вектор 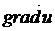, направленный по нормали к поверхности уровня поля и численно равный наибольшей производной по направлению. Если в пространстве выбрана некоторая декартовая система координат, то 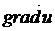вычисляется по формуле

.

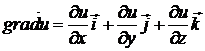Модуль вектора 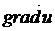есть наибольшая скорост