Модуль действительного числа
Определение.Модулем действительного числа х называется неотрицательное число, определяемое условием
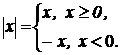
Если e > 0 - произвольное число, то из неравенства 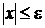 следует, что
следует, что 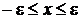 или
или 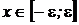 .
.
Свойства модуля действительного числа
Пусть а и b – произвольные действительные числа. Тогда:
1. 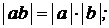 2.
2. 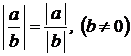 ;
;
3.  – неравенство Коши – Буняковского; 4.
– неравенство Коши – Буняковского; 4. 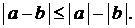
Ограниченные множества
Определение. Множество DÌ Rназывается ограниченным сверху, если существует такое действительное число b, что х £ b, " хÎ D. Аналогично - D ограничено снизу, если существует такое действительное число а, что х ³ а, " хÎ D.
Определение. Множество Dназывается ограниченным, если оно ограничено сверху и снизу, то есть множество D ограничено в том и только в том случае, если оно расположено на конечном отрезке [а; b] (рис.4.1).

Множество, состоящее из конечного числа точек - ограничено.
Примеры:
1. Множество натуральных чисел ограничено снизу любым числом а £ 1.
2. Множество отрицательных чисел ограничено сверху любым числом
b ³ 0.
Определение. Множество неограниченное сверху или снизу называется неограниченным.
Теорема:множество DÌ R–неограниченно, если " М > 0 $ хÎ D, такое что çх ç> М.
Например, множество целых чисел Z неограниченно. Неограниченными множествами являются бесконечные интервалы (-¥; +¥), (-¥; b), (а; +¥).
Нижние и верхние грани множества
Если действительное число b ограничивает множество D сверху, то b называется верхней гранью множества D. Любое число больше b, тоже является верхней гранью множества D.
Наименьшая верхняя грань множества D называется точной верхней гранью и обозначается sup D = M или sup{x} = M(латинское слово supremum - наибольший).
Из определения точной верхней грани вытекают следующие свойства:
Mесть верхняя грань множества D, то есть " хÎ D выполняется неравенство х £ M;
" e > 0 найдется число хÎ D, такое, что M – e < х £ M.
Аналогично определяется точная нижняя грань множества D.Наибольшая нижняя грань множестваDназывается точной нижней гранью и обозначается
inf D= m или inf{x} = m (латинское слово infimum - наименьший).
Точная нижняя грань mмножестваD характеризуется свойствами:
m есть нижняя грань множестваD, то есть " хÎ D выполнено неравенство х ³ m;
" e > 0 найдется число хÎ D, такое, что m < х £ m + e.
Принадлежность множеству D верхней и нижней грани необязательна. Существование inf Dи sup D у ограниченного множества очевидно.
Точной верхней гранью неограниченного множества является (+¥). Точной нижней гранью неограниченного множества является (–¥).
Например, sup [a; + ¥) = +¥, inf (–¥; b] = –¥, sup Z = +¥, inf Z = –¥.
Окрестность точки
Определение.Расстоянием между числами х1 и х2 называется число r(х1, х2) = êх1 - х2 ê.
Определение.e - окрестностью точки aÎ R., называется множество действительных чисел
Ue(a) = r (х, a) = êх - a ê< e (рис.4.2).
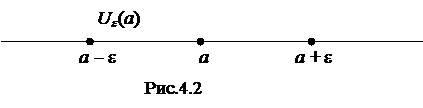
Проколотой окрестностью называется окрестность, из которой удалена сама точка a (рис.4.3).

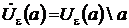
Комплексные числа
