Расстояние от точки до плоскости

Расстояние от точки М₀(x₀;y₀;z₀) до плоскости, заданной общим уравнением (1.22) находится по формуле

.

Уравнение плоскости в отрезках

Если общее уравнение плоскости (3.22) разделить на , то получим уравнение плоскости в отрезках

(3.23)

В уравнении (3.23) и – координаты точек пересечения плоскости (3.22) с осями координат Ох, Оy и Оz, соответственно (рис.3.11).

Уравнение плоскости, проходящей через три точки

Пусть даны три точки M₁(x₁;y₁;z₁), M₂(x₂;y₂;z₂) и M₃(x₃;y₃;z₃). Тогда векторное уравнение плоскости, проходящей через три точки, будет иметь вид:

,

где радиус–векторы точек плоскости, точка М(x;y;z) – произвольная точка плоскости. из условия компланарности трех векторов (свойство смешанного произведения) следует уравнение плоскости. В координатной форме это уравнение примет вид

(3.24)

Пример:

Составить уравнение плоскости Q, проходящей через точку М₀(–2;3;2), параллельно двум векторам и

Решение:пусть М(x;y;z) – текущая точка плоскости. Векторы и компланарны относительно плоскости Q. Из условия компланарности трех векторов (3.24) получим векторное уравнение плоскости Q. В координатной форме уравнение плоскости Q будет иметь вид

или 2х + 7у + 3 z – 23 = 0 .

Пример:

Составить уравнение плоскости, проходящей через три точки М₁(–2;–4;2), М₂(3;–1;0), М₃(1;5;–2).

Решение:пусть М(x;y;z) – текущая точка плоскости. тогда, применяя формулу (3.24), получим

или 2х + 7у + 18z – 2 = 0.

Взаимное расположение плоскостей

Пусть даны две плоскости А₁х+В₁у+С₁z +D₁ = 0 и А₂х+В₂у+С₂z +D₂ =0. Тогда угол φ между этими плоскостями определяется по формуле

из которой следует условие параллельности плоскостей

и их перпендикулярности

.

Пример:

найти угол  между плоскостями

3х – 5у + 8z – 2 = 0 и 5х + 4у – 3z + 7 = 0.

Решение:

.

Прямая линия в пространстве

1. Поскольку прямую можно трактовать, как линию пересечения двух плоскостей, то её можно задать системой уравнений двух плоскостей

2. Как и на плоскости, прямую линию в пространстве можно задать координатами двух точек M₁(x₁;y₁;z₁) и M₂(x₂;y₂;z₂). Уравнения прямой находим из условия коллинеарности двух векторов и в виде

, (3.25)

где M(x;y;z) – текущая точка на прямой линии.

3. В уравнениях (3.25) введем обозначения . Тогда вектор можно рассматривать как проекции вектора, параллельного прямой М₁М₂. Из условия коллинеарности двух векторов и получим канонические уравнения прямой

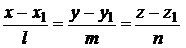. (3.26)

Вектор называется направляющим вектором прямой.

Полученная прямая линия (3.26) проходит через точку M₁(x₁;y₁;z₁) и образует с осями координат углы α, β и γ, косинусы которых определяются по формулам

.

4. Канонические уравнения преобразуется в параметрические уравнения прямой .

Пример:

Привести к каноническому виду уравнения прямой линии

Решение: определим координаты какой-либо точки на прямой линии. Для этого положим в обоих уравнениях z = 0:

Отсюда определим х = 2 и у = – 1. Таким образом, получим точку М₀(2; –1;0). Направляющий вектор , где и . Таким образом,

.

По формуле (3.26) найдем канонические уравнения:

, или .