Свойства произведения матриц

1. В общем случае АВ ≠ ВА.

2. Если А согласуется с В, а В согласуется с С, то

(АВ)С = А(ВС) и (А+В)С = АС +ВС.

3. АЕ = ЕА = А, где Е – единичная матрица.

Обратная матрица

Определение.Матрица А^–1 называется обратной матрицей для матрицы А, если выполняется равенство:

А∙А^-1 = А^-1∙А = Е,

где Е – единичная матрица.

Обратной матрицей обладают квадратные матрицы, определитель которых отличен от нуля (невырожденные матрицы). Обратная матрица у вырожденных матриц не существует.

Порядок нахождения обратной матрицы

1. Вычислить определитель матрицы А, то есть найти |А|.

2. Найти все алгебраические дополнения А_ij для элементов матрицы А.

3. Из алгебраических дополнений А_ij составить матрицу С: с_ij = А_ij и транспонировать её, то есть найти С^Т.

4. Записать ответ в виде 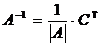или

.

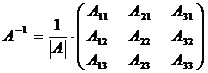Пример:

Найти А^-1, если .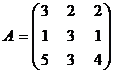

Решение: 1. Вычислим определитель матрицы

.

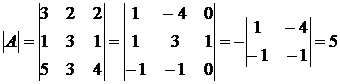2. Найдем алгебраические дополнения для матрицы А:

; ; ; ;

; ; ; .

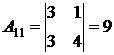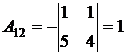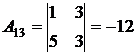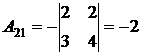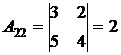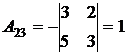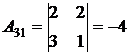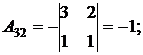
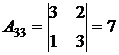3. Из А_ij составим матрицу С и транспонируем её:

;

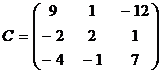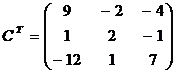
Ответ: .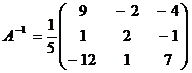

Обратная матрица на компьютере Excell вычисляется по команде "=МОБР()" в виде скрытого массива. Доступ к элементу с_i,j обратной матрицы даёт команда "=ИНДЕКС(МОБР();i;j)"

Матричное представление системы линейных уравнений

Если из коэффициентов при неизвестных системы линейных уравнений

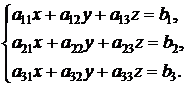
составить матрицу А, из неизвестных величин матрицу Х, а из чисел правой части уравнений матрицу В, то система линейных уравнений запишется в виде матричного уравнения (1.5)

АХ = В, (1.5)

где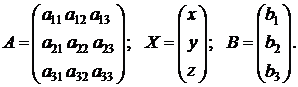

Решение СЛУ матричным способом

Умножив обе части уравнения (1.5) на А^–1, получим:

А^–1∙АХ = А^–1∙В

Поскольку произведение А^–1∙А = Е, а произведение ЕХ = Х, то

Х = А^–1∙В.

Как и для метода Крамера, матричный способ требует равенства числа неизвестных числу уравнений и неравенства нулю определителя матрицы А.

Пример:

Решить систему уравнений: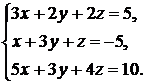

Решение: по данной системе составляем матрицы:

; ; .

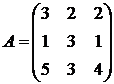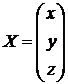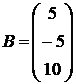Матрица А^–1 вычислена в предыдущем примере, поэтому сразу находим матрицу Х:

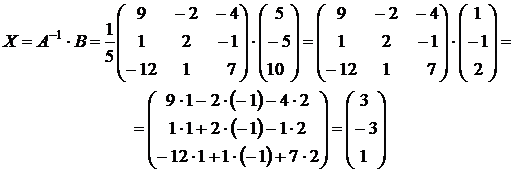
Ответ: x = 3; y = ^–3; z = 1.

Исследование СЛУ

Элементарные преобразования матрицы. Ранг матрицы

Элементарными преобразованиями матрицы А называются:

1) перестановка двух строк матрицы;

2) вычёркивание строки состоящей исключительно из нулей;

3) умножение какой-либо строки на число λ ≠ 0;

4) линейное преобразование строки матрицы, которое означает сложение элементов одной строки с соответствующими элементами другой строки, умноженных на число λ ≠ 0.

Аналогичные элементарные преобразования матрицы можно выполнять и со столбцами матрицы.

С помощью элементарных преобразований любую матрицу можно привести к специальному виду, где на главной диагонали стоит r единиц формула (1.6).

Число r единиц, стоящих на главной диагонали, не зависит от способа приведения матрицы А к виду А_r и называется рангом матрицы А и обозначается r = rang A .

Матрицы, полученные друг из друга элементарными преобразованиями, не меняют ранга и называются эквивалентными матрицами: А ~ А_r.

Эквивалентные матрицы имеют равные ранги.

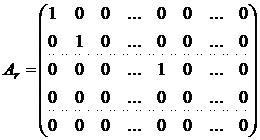. (1.6)

Пример:

Найти ранг матрицы .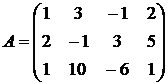

Решение:выполняя элементарные преобразования над данной матрицей, получим следующую систему эквивалентных матриц:

~ ~ ~

~ ~ ~ ~ .

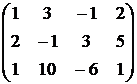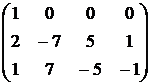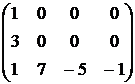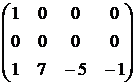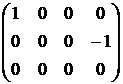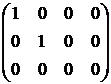Следовательно, ранг матрицы А равен 2.

Ответ: r = 2.