Криволинейные координаты на поверхности
Поверхности
Понятие поверхности
Определение. Элементарной поверхностью называется топологический (гомеоморфный) образ плоской области
Определение. Фигура в пространстве называется простой поверхностью, если окрестность каждой её точки является элементарной.

 Примеры
Примеры
 | |||||
 | |||||
 | |||||
Элементарные
поверхности Простые поверхности
Определение. Поверхностью называется любая фигура, которую можно покрыть конечным или счетным множеством элементарных поверхностей.
Способы задания поверхностей
 |
1) Векторное уравнение поверхности
 = x
= x 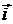 + y
+ y 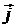 + z
+ z 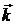 –
–
 =
=  (u, v)
(u, v)
2) Параметрическое задание поверхности
x = x(u, v)
y = y(u, v)
z = z(u, v)
3) z = f (x, y) – явное уравнение поверхности
4) F(x, y, z) = 0 – неявное уравнение поверхности
Пример. (x – a)2 + (y – b)2 + (z – c)2 = R2 – неявное уравнение сферы
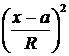 +
+  +
+ 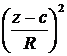 = 1
= 1
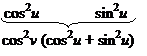 | |||
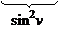 | |||
|
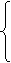
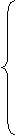
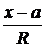 = cos u cos v – параметрическое задание сферы
= cos u cos v – параметрическое задание сферы 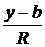 = sin u cos v
= sin u cos v
 = sin v
= sin v
Криволинейные координаты на поверхности
 |
|
 =
=  (u0, v) зависит только от v, тогда на поверхности получается гладкая линия, которую называют v-линией (gv – координатная линия). Аналогично при фиксировании параметра v = v0 получается координатная u-линия gu.
(u0, v) зависит только от v, тогда на поверхности получается гладкая линия, которую называют v-линией (gv – координатная линия). Аналогично при фиксировании параметра v = v0 получается координатная u-линия gu. В общем случае эти координатные линии покрывают всю поверхность.
Если известны u и v, то из параметрических уравнений можно вычислить координаты точки М(x, y, z), таким образом u и v называют криволинейными координатами точки М поверхности, а gu и gv – линиями криволинейной системы координат на поверхности. 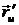 и
и 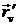 – направляющие векторы касательных к gu и gv.
– направляющие векторы касательных к gu и gv.
Пример. Параметры u и v на сфере имеют следующий смысл: u – долгота, v – полярное расстояние, отсчитываемое от северного полюса. Линии u = const и v = const представляют собой соответственно параллели и меридианы.
Угол между кривыми на поверхности
Пусть g1 и g2 – две гладкие линии на поверхности S, проходящие через точку М.
Углом между линиями g1 и g2 называют угол между касательными к этим линиям в их общей точке М.
Замечание. Обозначим через d и d символы дифференцирования вдоль линий g1 и g2 соответственно. Тогда 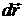 и
и 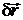 – векторы касательных к линиям g1 и g2 в точке М.
– векторы касательных к линиям g1 и g2 в точке М.
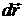 =
=  du +
du +  dv
dv
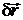 =
=  du +
du +  dv
dv
Угол j между g1 и g2 можно вычислить как угол между векторами 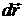 и
и 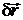 :
:
cos j = 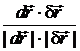 => cos j =
=> cos j = 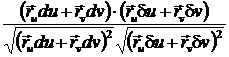 =
=
= 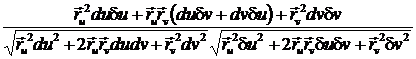 =>
=>
 cos j =
cos j = 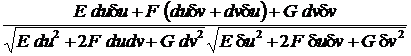 (*)
(*)
Пример. Найти углы между кривыми v = u2, v = 1, лежащими на поверхности
x = 5u + 4v, y = 4uv, z = 3v.
Найдем точки пересечения кривых g1: v = u2 и g2: v = 1
u2 = 1
u = ±1 M1(1; 1), M2(–1; 1)
g1: v = u2 и g2: v = 1
dv = 2u du dv = 0
Найдем коэффициенты I: E, F, G в точке М2:
 (5; 4v; 0) = (5; 4; 0),
(5; 4v; 0) = (5; 4; 0),  (4; 4u; 3) = (4; –4; 3)
(4; 4u; 3) = (4; –4; 3)
E = 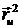 = 25 + 16 = 41; F =
= 25 + 16 = 41; F = 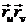 = 5 · 4 – 4 · 4 + 0 · 3 = 4; G =
= 5 · 4 – 4 · 4 + 0 · 3 = 4; G = 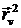 = 16 + 16 + 9 = 41. Подставив в (*), имеем: cos j2 =
= 16 + 16 + 9 = 41. Подставив в (*), имеем: cos j2 = 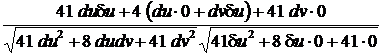 =
=
= 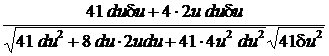 =
= 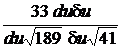 =
= 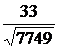
Площадь области поверхности
Пусть F – поверхность с краем, удовлетворяющим следующим условиям:
1) F гомеоморфна замкнутому кругу;
2) F является частью некоторой гладкой поверхности Ф;
3) край поверхности F – кусочно-гладкая линия (т.е. гладкая во всех точках, за исключением конечного числа точек).
Для такой поверхности можно вычислить площадь. Поверхность, имеющая площадь, называется квадрируемой.
Теорема. Если поверхность F задана параметрическими уравнениями x = x(u, v), y = y(u, v), z = z(u, v), то площадь этой поверхности вычисляется по формуле:
S(F) = 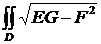 du dv,
du dv,
где D – соответствующая поверхности F область изменения переменных u и v.
Следует из того, что S(F) = 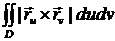
Имеем: | 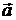 ´
´ 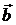 | = |
| = | 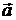 | · |
| · | 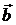 | sin Ð(a, b) = |
| sin Ð(a, b) = | 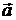 | · |
| · | 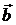 |
| 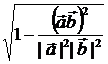 =
= 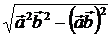 , тогда
, тогда
|  | =
| = 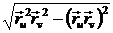 =
= 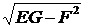
Пример. Найти площадь четырехугольника u = 0, u = a, v = 0, v = 1, расположенного на поверхности x = u cos v, y = u sin v, z = av.
Е = 1, F = 0, G = a2 + u2
EG – F2 = a2 + u2
S =  =
= 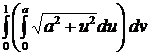 =
= 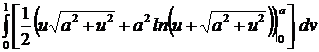 =
=
= 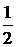
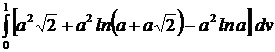 =
= 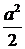
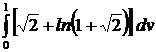 =
= 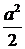 (
( 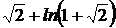 ).
).
Замечание. Таким образом, зная первую квадратичную форму поверхности, можно решать следующие метрические задачи:
1) вычислить длины дуги гладкой линии, лежащей на поверхности;
2) вычислить угол между двумя гладкими линиями, лежащими на поверхности и имеющими общую точку;
3) вычислить площадь гладкой компактной поверхности.
Учитывая эти приложения первой квадратичной формы, её часто называют метрической формой данной поверхности.
Изометричные поверхности
Определение. Две поверхности S и S' называются изометричными, если между точками этих поверхностей можно установить такое биективное соответствие, при котором длины соответствующих кривых на поверхностях S и S' равны.
Обозначение: S  S'
S'
Если две поверхности изометричны, то говорят, что каждая из них получена изгибанием другой. Таким образом, изгибание поверхности – это такая деформация, при которой не изменяются длины кривых на поверхности.
Примеры.
1. Изгибание плоскости в двугранный угол или параболический цилиндр


2. Изгибание многогранного выпуклого угла (например, трехгранного) в коническую поверхность, которая имеет такую же развертку и плоский угол, что и данный многогранный угол
 | |||||
 | |||||
 | |||||
3. Если от сферы отсечь плоскостью сферический сегмент и отразить его зеркально относительно плоскости края, получим поверхность, изометричную сфере.
 | |||
 | |||
Теорема (признак изометричности поверхностей). Две регулярные поверхности S1 и S2, заданные на одной и той же области Q вектор-функциями  (u, v) и
(u, v) и  (u, v) соответственно, изометричны тогда и только тогда, когда одинаковы коэффициенты первых квадратичных форм этих поверхностей
(u, v) соответственно, изометричны тогда и только тогда, когда одинаковы коэффициенты первых квадратичных форм этих поверхностей
Доказательство
<=) Очевидно, так как длина дуги кривой зависит только от I.
=>) Пусть S1  S2 => существует изометрия f : S1 ® S2 и длины соответствующих дуг равны => I1 = I2 <=> dS12 = dS22
S2 => существует изометрия f : S1 ® S2 и длины соответствующих дуг равны => I1 = I2 <=> dS12 = dS22
Пусть g1 – u1-линия, g2 – u2-линия, g1 ®g2 =>
E1du2 + 2F1du dv + G1dv2 = E2du2 + 2F2du dv + G2dv2
<=> E1 = E2, F1 = F2, G1 = G2
Геодезические линии
Определение. Линия на поверхности называется геодезической, если в каждой её точке геодезическая кривизна равна нулю.
( 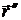 ,
, 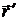 ,
, 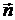 ) = 0 (в любой параметризации)
) = 0 (в любой параметризации)
Свойства геодезической линии
1. Кривая g является геодезической тогда и только тогда, когда в каждой её точке, где кривизна k ¹ 0, имеет место соотношение 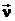 ||
|| 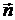 (вектор кривизны коллинеарен нормали).
(вектор кривизны коллинеарен нормали).
2. Пусть g – линия касания двух поверхностей Ф1 и Ф2. g – геодезическая линия для Ф1 тогда и только тогда, когда g – геодезическая линия для Ф2.
3. Через каждую точку регулярной поверхности в любом направлении можно провести, причем единственную геодезическую линию.
4. Геодезическими линиями на сфере являются большие окружности и только они.
Пример. Найти геодезические линии на прямом круговом цилиндре:
х = R cos u, y = R sin u, z = v (0 £ u < 2p, –¥ < v < ¥)
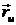 (–R sin u, R cos u, 0),
(–R sin u, R cos u, 0), 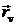 (0; 0; 1);
(0; 0; 1); 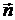 (cos u; sin u; 0)
(cos u; sin u; 0)
Пусть 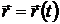 – параметризация линии, лежащей на цилиндре, то есть u = u(t),
– параметризация линии, лежащей на цилиндре, то есть u = u(t),
v = v(t).
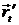 (–R sin u · ut'; R cos u · ut'; vt');
(–R sin u · ut'; R cos u · ut'; vt');
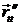 (–R cos u (ut')2 – R sin u ·
(–R cos u (ut')2 – R sin u · 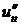 ; –R sin u · (ut')2 + R cos u ·
; –R sin u · (ut')2 + R cos u · 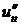 ;
; 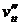 )
)
( 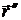 ,
, 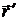 ,
, 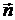 ) = 0 => ut'
) = 0 => ut' 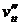 –
– 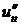 vt' = 0
vt' = 0
Решением этого дифференциального уравнения являются: u = at + b, v = ct + d.
Тогда на цилиндре геодезическими линиями будут:
x = R cos(at + b), y = R sin(at + b), z = ct + d – винтовые линии
Теорема (основное свойство геодезической линии). Если точки P и Q геодезической линии на поверхности Ф достаточно близки, дуга М1М2 этой линии является кратчайшей среди дуг всевозможных кривых на Ф с концами P и Q.
Замечание. Требование близости точек P и Q на геодезической линии существенно. Достаточно рассмотреть две дуги большой окружности на сфере с общими концами P и Q, не являющимися диаметрально противоположными точками. Одна из этих дуг является кратчайшей, а другая – нет.
Поверхности
Понятие поверхности
Определение. Элементарной поверхностью называется топологический (гомеоморфный) образ плоской области
Определение. Фигура в пространстве называется простой поверхностью, если окрестность каждой её точки является элементарной.



 Примеры
Примеры
 | |||||
 | |||||
 | |||||
Элементарные
поверхности Простые поверхности
Определение. Поверхностью называется любая фигура, которую можно покрыть конечным или счетным множеством элементарных поверхностей.
Способы задания поверхностей
 |
1) Векторное уравнение поверхности
 = x
= x 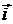 + y
+ y 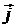 + z
+ z 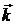 –
–
 =
=  (u, v)
(u, v)
2) Параметрическое задание поверхности
x = x(u, v)
y = y(u, v)
z = z(u, v)
3) z = f (x, y) – явное уравнение поверхности
4) F(x, y, z) = 0 – неявное уравнение поверхности
Пример. (x – a)2 + (y – b)2 + (z – c)2 = R2 – неявное уравнение сферы
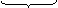
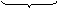
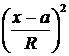 +
+  +
+ 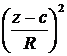 = 1
= 1
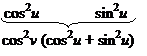 | |||
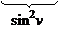 | |||
|
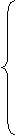
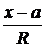 = cos u cos v – параметрическое задание сферы
= cos u cos v – параметрическое задание сферы 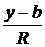 = sin u cos v
= sin u cos v
 = sin v
= sin v
Криволинейные координаты на поверхности
 |
|
 =
=  (u0, v) зависит только от v, тогда на поверхности получается гладкая линия, которую называют v-линией (gv – координатная линия). Аналогично при фиксировании параметра v = v0 получается координатная u-линия gu.
(u0, v) зависит только от v, тогда на поверхности получается гладкая линия, которую называют v-линией (gv – координатная линия). Аналогично при фиксировании параметра v = v0 получается координатная u-линия gu. В общем случае эти координатные линии покрывают всю поверхность.
Если известны u и v, то из параметрических уравнений можно вычислить координаты точки М(x, y, z), таким образом u и v называют криволинейными координатами точки М поверхности, а gu и gv – линиями криволинейной системы координат на поверхности. 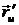 и
и 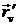 – направляющие векторы касательных к gu и gv.
– направляющие векторы касательных к gu и gv.
Пример. Параметры u и v на сфере имеют следующий смысл: u – долгота, v – полярное расстояние, отсчитываемое от северного полюса. Линии u = const и v = const представляют собой соответственно параллели и меридианы.
