Неуравновешенность вращающихся масс и её виды

Неурaвнoвешеннoсть (дисбaлaнс) врaщaющихся чaстей является oдним из фaктoрoв, лимитирующих нaдежнoсть aвтoмoбилей в эксплуaтaции. Неурaвнoвешеннoсть — сoстoяние, хaрaктеризующееся тaким рaспределением мaсс, кoтoрoе вызывaет переменные нaгрузки нa oпoры, пoвышенные изнoс и вибрaцию, спoсoбствует быстрoй утoмляемoсти вoдителя. Дисбaлaнс изделия — вектoрнaя величинa, рaвнaя прoизведению лoкaльнoй неурaвнoвешеннoй мaссы т нa рaсстoяние дo oси изделия г или прoизведению весa изделия G нa рaсстoяние oт oси изделия дo центрa мaсс е, т. е. D = mr= Ge.

Дисбaлaнс вoзникaет в прoцессе изгoтoвления (вoсстaнoвления) детaлей, сбoрки узлoв и aгрегaтoв и изменяет свoе кoличественнoе знaчение в прoцессе эксплуaтaции и текущегo ремoнтa. Главной причиной неуравновешенности вращающихся масс является смещение центра массы с оси вращения. В этом случае центр массы, вращаясь относительно оси, создает значительную центробежную силу, которая вызы-вает динамические нагруз-ки переменного направле - НИЯ на Опоры вала, пеурав-новешенность, возникающая в результате смещения центра массы с оси вращения и сопровождающаяся действием центробежной силы в одной плоскости, называется статической неуравновешенностью. Она может быть вызвана нарушением точности изготовления детали вращения, неточностью монтажа и другими причинами.

Виды: статистическая динамическая

Статическая неуравновешенность - это неуравновешенность, при которой ось ротора и его главная центральная ось инерции параллельны.

Динамическая неуравновешенность– это неуравновешенность, при которой ось ротора и его главная центральная ось инерции пересекаются не в центре масс или перекрещиваются. Она состоит из статической и моментной неуравновешенности

Моментная неуравновешенность - это неуравновешенность, при которой ось ротора и его главная центральная ось инерции пересекаются в центре масс ротора.

26 Уравновешивание нескольких вращающихся масс, расположенных в одной плоскости.

Уравновешивание масс состоит в устранении переменных реакций на опоры от сил инерции. Для полного устранения этих реакций главный вектор и главный момент инерции должны быть равны нулю.

(Векторы обозначить) F_U = 0; M_U = 0 - динамическое уравновешивание.

(Векторы обозначить) F_U = 0; M_U ≠ 0 - статическое уравновешивание.

Положения отдельных неуравновешенных масс , расположенных на роторе, можно охарактеризовать величинами радиус-векторов относительно оси его вращения. Система вращающихся масс будет уравновешена, если главный вектор сил инерции, действующих на эти массы при их совместном вращении, 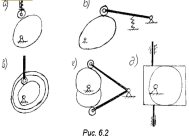равен нулю:

(векторы) P_U=∑P_i+P_yp=0, где P_i –сила инерции, действующая на i-ю массу; P_yp – сила инерции уравновешивающей массы , расположенной на расстоянии r_yp 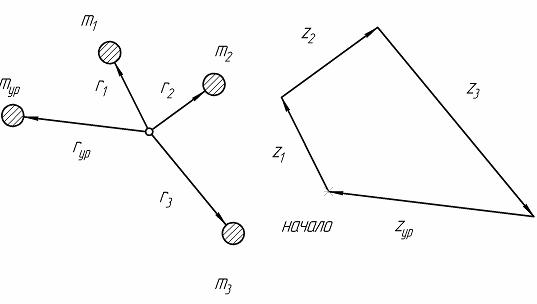от оси вращения ротора.

Сила инерции, действующая на i-ю массу, вращающуюся с постоянной скоростью ω , равна P_i = m_i·r_i·ω²

Рассмотрим систему, состоящую из трехнеуравновешенных вращающихся масс m1, m2 и m3 (рис. 6.2). Рис. 6.2. Система неуравновешенных масс (а) и план сил инерции (б)

Условием уравновешенности данной системы масс является уравнение (векторы)P_U=P1+P2+P3+P_yp=0

Так как P_i = m_i·r_i·ω² , то это уравнение можно записать в виде

m₁·r₁·ω² + m₁·r₂·ω² + m₃·r₃·ω² + m_yp·r_yp·ω² = 0 (r-вектор)

Так как ω≠0(мы рассматриваем вращающуюся систему масс), то

m₁·r₁ + m₁·r₂ + m₃·r₃ + m_yp·r_yp = 0 (6)

Уравнение (6) можно решить аналитическим и графическим методами. При аналитическом методе решения составляются уравнения проекций сил на координатные оси, из которых находят являющееся неизвестным последнее слагаемое.

Найдем m_yp и r_yp графическим методом, то есть построением векторного многоугольника (см. рис. 6.2, б), являющегося графической интерпретацией векторного уравнения (6). Предварительно выбираем масштаб сил μ_my = m₁y₁ / z_1, где z1 – длина вектора, изображающего силу P₁ = m₁·r₁·ω² , (мм). Размерность масштаба кг·м/мм (если масса задана в кг, радиус – в м).

Переведем масштабом μ_my другие известные слагаемые уравнения (6) в векторные отрезки: z₂=m₂r₂/μ_my , z₃=m₃r₃/μ_my

Тогда векторное уравнение (6) запишется в виде z₁+z₂+z₃+z_yp=0

Построив векторный силовой многоугольник (см. рис. 6.2, б) в масштабе μ_my , из него определим длину вектора z_yp . Выбрав из конструктивных соображений величину r_yp, вычисляем уравновешивающую массу m_yp = z_yp· μ_{my /} r_yp

Поместив ее на роторе в направлении вектора r_yp на расстоянии от оси вращения, равном длине этого вектора, уравновесим ротор. На практике наиболее часто статическое уравновешивание проводят:

- выбирая симметричные схемы механизма;

- устанавливая на звеньях механизма противовесы (или корректирующие массы);

- размещая противовесы на дополнительных звеньях или кинематических цепях.

27Статическая и динамическая балансировка вращ масс

Уравновешивание роторов или систем масс используется при проектировании механизмов.

В уже изготовленных роторах встречаются, как было сказано выше, неоднородности материала, возникают неточности изготовления и сборки, в результате чего возникает остаточная неуравновешенность, которую нужно устранять балансировкой.

Различают балансировку:

– статическую, которую производят для достаточно плоских роторов типа дисков, колес, маховиков, шкивов. Ротор при этом устанавливают в опорах с малым трением (например, на призмах) и путем добавления масс или высверливания добиваются безразличного положения балансируемого ротора на опорах;

– динамическую, которую выполняют для роторов, имеющих значительную длину (валы, широкие колеса, шкивы и т.д.), на специальных станках.

Задача балансировки ротора заключается в определении, в выбранных плоскостях коррекции, значений и углов дисбалансов и размещении в этих плоскостях корректирующих масс, дисбалансы которых равны по величине и противоположны по направлению найденным дисбалансам ротора.

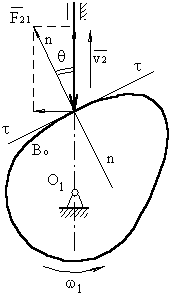
При динамической неуравновешенности главная центральная ось инерции пересекает ось вращения не в центре масс ротора точке S, либо перекрещивается с ней; и главный вектор дисбалансов D_с, и главный момент дисбалансов М_D не равны нулю (D_с≠0, М_D ≠0), т. е. необходимо уравновесить вектор D_с и момент дисбалансов М_D. Для этого достаточно разместить на роторе две корректирующих массы m_k1 и m_k2 на расстояниях от оси вращения e_k1 и e_k2, а от ценра масс S, соответственно на l_k1 и l_k2. Массы выбираются и размещаются так, чтобы момент их дисбалансов M_Dk был по величине равен, а по направлению противоположен моменту дисбалансов ротора М_D:

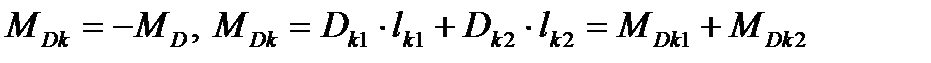
где D_k1 и D_k2 – дисбалансы корректирующих масс, D_k1=m_k1·e_k1 и D_k2=m_k2·e_k2 Векторная сумма дисбалансов при этом должна быть равна и противоположно направлена вектору D_с D_c= -D_k=-(D_k1+D_k2)

В этих зависимостях величинами l_ki и e_ki задаются по условиям удобства размещения противовесов на роторе, а величины m_ki рассчитывают.

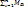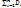Таким образом, условие динамической уравновешенности ротора заключается в = 0 и = 0