Системы диагноза технического состояния деталей и оборудования.

Объекты диагноза.

Для построения математических моделей объектов диагноза в процессе проектирования и создания систем диагноза необходимо знать физические свойства и характеристики этих объектов.

В получении таких знаний важное место занимает изучение возможных физических неисправностей объекта, а также параметров, характеризующих исправное и все неисправные состояния объекта. При этом полезна классификация объектов по принципу их действия, по назначению, по сложности, по энергетическим и другим признакам. Необходимо также классифицировать неисправности по их видам (например, на производственные и эксплуатационные, на катастрофические и постепенные), определять вероятности или частности, анализировать причины их возникновения, разрабатывать методы определения признаков неисправностей и т.п. Работы по исследованию параметров объектов включают в себя разработку методов задания допусков и определения контрольных соотношений между отдельными параметрами, изучение вопросов точности измерения параметров при диагнозе, определение законов изменения параметров во времени и т.п.

Для построения оптимальных алгоритмов диагноза большое значение имеет организация сбора и обработки статистических данных, особенно по вероятностям возникновения неисправностей и по затратам (времени, энергии, материальных или денежных средств и т. д.) на отыскание неисправностей и их устранение. Отметим, что статистические данные важны не только для оптимизации алгоритмов диагноза, но также для эффективного решения задач технической прогностики и технической генетики.

Объектами диагнозамогут быть любые технические изделия, устройства или системы, относительно которых имеет смысл ставить и решать задачи проверки их исправности, работоспособности, правильности функционирования или задачи поиска неисправностей.

Последствия любых явлений или действий, которые переводят объект в некоторое неисправное состояние, называются физическими неисправностямиобъекта.

Объект может состоять из компонент - функционально или конструктивно выделенных частей. Тогда совокупность компонент объекта, связей между компонентами (внутренних связей) и связей объекта с внешней средой (внешних связей) называют структуройобъекта. Понятия исправного и неисправного состояний, а также физической неисправности приложимы к компонентам объекта, его внутренним и внешним связям.

Взаимодействие объекта с внешней средой осуществляется через его основные и дополнительные входы и выходы. Сигналы на входах и выходах объекта характеризуются параметрами тех физических величин, с помощью которых передаются указанные сигналы. Это - входные и выходные параметрыобъекта. Часто возникает необходимость рассматривать внутренниепараметрыобъекта, т. е. такие параметры, которые не являются его входными или выходными. Например, необходимо замерить сопротивление резистора, снять напряжение на трансформаторе и т.д.

Последовательности (или, в частном случае, совокупности) возможных значений входных параметров образуют множество возможных воздействийна объект. Аналогично, множество ответовобъекта определяется последовательностью (или, в частном случае, совокупностью) значений его выходных параметров.

Таким образом, воздействие на объект (ответ объекта) характеризуется составом входов (выходов) и теми моментами времени, в которые поступают заданные (измеряются получаемые) значения параметров на этих входах (выходах). Последовательность (совокупность) значений указанных параметров можно называть значением воздействия (ответа).

Элементарная проверка представляет собой некоторый физический эксперимент над объектом и определяется значением воздействия, подаваемого или поступающего на объект, а также ответом объекта на это воздействие. Значение ответа объекта является результатом элементарной проверки. Ясно, что объект, находящийся в разных технических состояниях, может выдать разные результаты одной и той же элементарной проверки. Понятие элементарной проверки применимо также к отдельным компонентам объекта. В этом случае, естественно, предполагается доступность входов и выходов компонент, что может потребовать организации дополнительных входов и выходов объекта.

Средства диагноза.

Различают аппаратурные, программные и программно-аппаратурные средства диагноза (рис.7).

Рис. 7. Классификация средств диагноза

Под средствами диагностирования понимается совокупность технических устройств, предназначенных для съема, преобразования, хранения и представления (документирования, индикации) диагностической информации о контролируемых объектах.

В общем случае средства диагностирования позволяет решать следующие задачи технической эксплуатации:

- оценивать техническое состояние оборудования на различных этапах эксплуатации;

- определять место и причину отказа;

- контролировать правильность функционирования оборудования;

- накапливать и анализировать информацию о надежности с целью разработки и реализации мероприятий, направленных на поддержание надежности на заданном уровне, а также - с целью прогнозирования технического состояния.

Стоимость диагностирования.

Среднюю оперативную продолжительность диагностирования в общем случае опре-деляют по формуле

,

где Т_i- средняя оперативная продолжительность диагностирования объекта, находящегося в состоянии i. Величина Тi включает продолжительность выполнения как вспомогательных операций, так и собственно диагностирования; P_оi - априорная вероятность нахождения объекта диагностирования в состоянии i.

Оценку средней оперативной продолжительности диагностирования выполняют по формуле

,

где N - общее число испытаний системы диагностирования (диагностирований объекта); Т_ig - оперативная продолжительность диагностирования объекта, находящегося в состоянии i при g-ом испытании.

Средние оперативные трудозатраты на диагностирование в общем случае определяют по формуле

,

где Q_ОДi - средние оперативные трудозатраты на диагностирование объекта, находящегося в состоянии i.

Оценку средних оперативных трудозатрат на диагностирование выполняют по формуле

где N - общее число испытаний системы диагностирования (диагностирований объекта); Q_ОДig - оперативные трудозатраты на диагностирование объекта, находящегося в состоянии i при g-ом испытании.

Среднюю стоимость диагностирования S_д вычисляют по формуле

,

где C_oi - средняя стоимость диагностирования объекта, находящегося в состоянии i. Величина С_i включает амортизационные затраты диагностирования, затраты на эксплуатацию системы диагностирования и стоимость износа объекта диагностирования при его диагностировании.

Таблица функций неисправностей.

Совокупность функций (2.3) и (2.4) можно представить в табличной форме.

Обозначим множество технических состояний объекта символом E. Пусть обозначает его исправное состояние, а - его i - неисправное состояние. Каждому i-му неисправному состоянию соответствует неисправность из множества S, и наоборот.

Построим прямоугольную таблицу, в строках которой поставим элементарные проверки из множества П, а в столбцах – технические состояния e из множества Е, или что тоже , функции , , реализуемые объектом, находящимся в исправном или i-неисправном состоянии. Значение индекса i=0 относится к столбцу исправного состояния e. На пресечении столбцов и строк таблицы проставим результат элементарной проверки объекта, находящегося в техническом состоянии . Множество всех результатов , ; обозначим символом R. Очевидно, . Построенную таблицу будем называть таблицей функций неисправностей объекта диагноза.

R	Е
е0	…		…
П
…
…

Непосредственное использование данной таблицы часто бывает затрудненно, по причине высокой размерности таблицы. Однако как универсальная математическая модель объекта диагноза она очень наглядна и удобна для процедур построения и реализации алгоритмов диагноза.

Можно заметить, что задание таблицы эквивалентно заданию системы функций (2.3) и (2.4). Столбец задает поведение исправного объекта, т.е. функцию (2.3), а остальные ее столбцы – поведения неисправного объекта, т.е. функцию (2.4).

Для определенности примем, что множество П обладает свойством обнаружения неисправностей из множества S, т.е. для любой неисправности найдется хотя бы одна элементарная проверка , - такая, что , а также свойством различения всех неисправностей из множества S, т.е. для каждой пары неисправностей , , , найдется хотя бы одна элементарная проверка , такая, что

Как всякая математическая модель объекта диагноза таблица функций неисправностей нужна для построения алгоритмов диагноза и для построения физической модели объекта.

Изложим основные операции процесса построения алгоритма диагноза по таблице функций неисправностей.

Задание на построение алгоритма диагноза должно содержать сведения о требуемой глубине диагноза. Требуемую глубину диагноза можно задавать через фиксированное разбиение множестваЕ на непересекающихся подмножеств , где ν=1,2, …, λ .

Тогда проверке исправности, работоспособности или правильности функционирования соответствует минимальная глубина диагноза, при которой λ=2., причем E₁={ } и E₂={ }, i=1,2, ,…, |S|. При поиске неисправности с максимальной глубиной диагноза (т.е. с точностью до каждого одного технического состояния) λ=|S|+1; E₁={ }; E_ν={ }, i=1,2,…,|S|; ν=i+1. Промежуточные значения глубины диагноза характеризуются условием 2<λ<|S|+1.

Способ разбиения множестваЕ технических состояний объекта на подмножества является достаточно универсальным. Но он неудобен тогда, когда отсутствует соответствие такого разбиения разбиению объекта на конструктивные составные части. Значительно удобнее требуемую глубину диагноза задавать через разбиение множества конструктивных компонент объекта на непересекающиеся подмножества. Например, широко известно требование проведения диагноза с глубиной до сменного блока. Этот случай соответствует рассмотрению одиночных неисправностей объекта. Поэтому получаем λ=N+1, E₁={e₀}, E_ν=E_l. Где Е_l– подмножество технических состояний неисправностей каждого отдельного блока; N – количество сменных блоков, если в качестве последних принять неисправности каждого сменного блока. Иначе обстоит дело тогда, когда нельзя исключить возможность существования неисправности в нескольких блоках. В этом случае получаем 2^N-1 подмножеств технических состояний, т.е. (с учетом исправного состояния е) λ=2^N.

Основу любого алгоритма диагноза составляет совокупность (множество) Пвходящих в него элементарных проверок. Для того чтобы обеспечить требуемую глубину диагноза, эта совокупность должна различать каждую пару технических состояний, принадлежащих разным подмножествам Е_ν и Е_μ , хотя может не различать любую пару технических состояний, принадлежащих одному и тому же подмножеству Е_ν. Первое условие означает, что для каждой пары технических состояний , , принадлежащих разным подмножествам Е_ν и Е_μ, среди элементарных проверок совокупности П найдется хотя бы одна элементарная проверка , результаты и которой различны, т.е. . Совокупность П элементарных проверок алгоритма диагноза будем называть полной, если она обеспечивает проведение диагноза либо с заданной глубиной, либо с глубиной обеспечиваемой множеством П всех допустимых элементарных проверок. Совокупность П называется не избыточной, если удаление из нее одной элементарной проверки ведет к уменьшению глубины диагноза.

Построение по таблице функций неисправностей всех полных не избыточных совокупностей элементарных проверок П можно осуществить, выполнив 2 операции.

1. Просмотром всех возможных неупорядоченных пар столбцов таблицы выделить пары технических состояний, принадлежащих разным подмножествам Е_ν и Е_μ, и для каждой такой пары просмотром (перебором) всех строк таблицы определить подмножества элементарных проверок результаты и которых для технических состояний , , различны.

2. Перебором всех подмножеств , полученных в результате выполнения операции 1, найти все такие совокупности П элементарных проверок, чтобы в каждой из них для каждого подмножества нашлась хотя бы одна элементарная проверка , принадлежащая этому подмножеству .

Остановимся теперь на применении таблицы функций неисправностей при построении физической модели объекта в СД. Определение совокупности элементарных проверок, входящих в алгоритм диагноза, соответствует выделению определенной совокупности строк таблицы функций неисправности. Подтаблицу, образованную совокупностью строк, будем называть П-таблицей функций неисправностей. Нетрудно видеть, что П-таблица является заданием функций (2.6), (2.7), определяющих физическую модель объекта в средствах диагноза. При представлении физической модели объекта П-таблицей процесс расшифровки фактических результатов 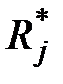элементарных проверок можно представить следующим образом. Каждая проверка выделяет строку П-таблицы, а ее фактический результат 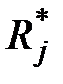делит множество столбцов таблицы на два подмножества. Те столбцы , i=1,2,…|S|, для которых , вычеркиваются из таблицы. Оставшиеся столбцы, для которых , представляют подмножество возможных технических состояний объекта. Завершению процесса диагноза соответствует момент, когда в таблице останется единственный не вычеркнутый столбец. Вычеркивание столбца означает, что объект диагноза неисправен.

Чем меньше число строк таблицы, тем проще процесс диагноза.

Сокращение размерности результатов элементарных проверок дает следующий прием. В каждой строке таблицы все результаты элементарной проверки, , удовлетворяющие условию , i=1,2,…|S|, принимаются равными 1, остальные результаты этой проверки, для которых имеет место неравенство , принимаются равными 0, независимо от того, различны они или одинаковы. При этом результат любой элементарной проверки может трактоваться только как положительный или как отрицательный . Упрощенную таблицу будем называть двоичной математической моделью объекта диагноза. Заметим, что в этой модели столбец , соответствующий исправному состоянию объекта, содержит только положительные результаты элементарных проверок.

Эффективных путей сокращения размеров таблицы нет. Она остается громоздкой и требует больших объемов вычислений. В этом состоит основная причина поиска и разработки различных более экономных способов представления и обработки информации. Платой является отказ от получения точных решений.

Алгоритмы диагноза.

Алгоритм диагноза задает совокупность элементарных проверок, последовательность их реализации и правила обработки результатов реализуемых элементарных проверок.

Результаты любой элементарной проверки могут быть использованы как признаки разбиения множестваЕ технических состояний объекта или подмножеств этого множества на классы. Любой алгоритм диагноза можно представить некоторым ориентированным графом. Ограничимся случаем, когда граф, представляющий алгоритм диагноза является деревом.

Дерево имеет вершины двух типов: вершины, из которых исходит хотя бы одна дуга, и вершины, из которых не отходит ни одной дуги.

Пример дерева дан на рис.6, где вершины первого типа представлены зачерненными кружками, а вершины второго типа – светлыми. В дереве имеется единственная вершина первого типа, в которую не заходит ни одна дуга. Эта вершина называется начальной, или корнем дерева (t₀, E). Вершины, из которых не исходит ни одной дуги, называются конечными, или висячими. Остальные вершины дерева называются внутренними. В каждую вершину дерева, кроме его корня, заходит только одна дуга. В дереве нет контуров.

Рангом вершины дерева называется число дуг пути, начинающегося в начальной вершине и заканчивающегося в рассматриваемой вершине. Минимальным рангом 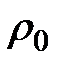дерева является ранг, для которого существует хотя бы одна висящая вершина и не существует ни одной висящей вершины ранга меньше 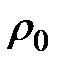. Максимальным рангом 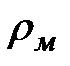дерева является ранг, для которого существует хотя бы одна вершина ранга 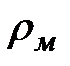и не существует ни одной вершины ранга больше .

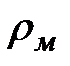Рис. 6. Дерево алгоритма диагноза

Будем внутренние и висящие вершины дерева нумеровать парой чисел в скобках(ρ, σ),где ρ – есть ранг вершины, а σ – ее порядковый номер среди всех вершин одного и того же ранга (например, слева направо). Начальную вершину будем обозначать парой (0,0). Начальной и внутренней вершине сопоставим элементарные проверки множества П. Дугам дерева, исходящей из некоторой его вершины, сопоставим возможные результаты проверки, представляемой этой вершиной. Начальной вершине поставим в соответствие множествоЕвозможных технических состояний объекта, а внутренним и висящим вершинам – подмножества технических состояний, получаемые как классы разбиений по результатам соответствующих элементарных проверок. Элементарную проверку и подмножество технических состояний, сопоставляемые вершине(ρ, σ)дерева будем обозначать символам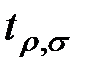и и 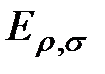соответственно. Множество элементарных проверок 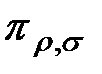обозначим символом П_д. Из правил построения дерева следует, что объединение множества технических состояний есть множествоЕвозможных технических состояний. Каждому пути соответствует последовательность элементарных проверок.

Рассмотрим, как дерево представляет алгоритм диагноза. Начальной вершине соответствует элементарная проверка 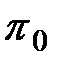множествоЕ всех возможных технических состояний. Элементарная проверка имеет три возможные результата, и тем самым разбивает множествоЕ на три подмножества Е_1,1, Е_1,2, Е_1,3 не различаемых этой проверкой технических состояний. Первые два из этих подмножеств соответствуют внутренним вершинам (1,1) и (1,2) и подлежат дальнейшим разбиениям элементарными проверкам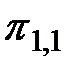и и 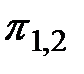. Третье подмножество соответствует висящей вершине, и поэтому разбиение его на подмножества алгоритмом не предусмотрено. Аналогично можно рассмотреть любую другую вершину дерева. Как только в процессе элементарных проверок будет достигнута висящая вершина, алгоритм диагноза прекращается. Фактическое техническое состояние объекта принадлежит подмножеству, соответствующему достигнутой висящей вершине. Каждой конкретной реализации алгоритма диагноза соответствует единственный путь. Например, если фактическое техническое состояние принадлежит подмножеству Е_3,2, то последовательность реализации элементарных проверок будет , , .

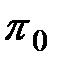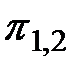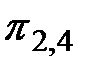Рассмотрим некоторый ненулевой ранг дерева. В общем случае дерево может иметь несколько внутренних вершин. Это значит, что возможны две разные последовательности реализации элементарных проверок. Обе эти проверки могут являться как одной и той же элементарной проверкой 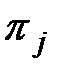множества П, так и разными элементарными проверками последнего. Если для каждого ранга дерева выполняется условие, состоящее том, что всем внутренним вершинам этого ранга сопоставлена одна и та же элементарная проверка из множества П, то алгоритм диагноза называется безусловным. Это соответствует заданию одной фиксированной последовательности реализации элементарных проверок из множества П, не зависящей от фактического технического состояния объекта. Т.е. выбор или назначение очередной элементарной проверки в последовательности их реализации не зависит от результатов предыдущих уже реализованных элементарных проверок. Если же в дереве найдется хотя бы один ранг с несколькими внутренними вершинами, которым сопоставимы разные элементарные проверки из множества П, то алгоритм диагноза называется условным. В условных алгоритмах выбор или назначение некоторых или всех (кроме 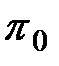) элементарных проверок производится с учетом результатов предыдущей уже реализованной элементарной проверки.

Достоинства безусловных алгоритмов: простота проверок, требуется хранить лишь состав элементарных проверок и единственную последовательность их реализации. Для условных требуется хранить кроме состава элементарных проверок все признаки безусловных и условных переходов от данной элементарной проверки к следующей, т.е. хранить не одну, а несколько последовательностей реализации элементарных проверок.

Безусловные алгоритмы диагноза можно классифицировать по характеру их остановки. Если выдача результатов диагноза предусмотрена только после реализации всех элементарных проверок, то алгоритм является алгоритмом с безусловной остановкой. Таким алгоритмам соответствуют деревья, у которых все висящие вершины имеют один и тот же ранг.

Во многих случаях фактическое техническое состояние объекта может быть определенно с требуемой глубиной диагноза прежде, чем будут реализованы все элементарные проверки алгоритма диагноза. Безусловные алгоритмы, у которых предусмотрена возможность выдачи результатов диагноза после реализации каждой элементарной проверки, называются алгоритмами с условной остановкой. Характерная особенность - не менее двух висящих вершин, ранги которых различны. Все условные алгоритмы являются алгоритмами с условной остановкой. Все указанные типы алгоритмов применяются в системах тестового диагноза. В системах функционального диагноза применяются алгоритмы с условной остановкой в связи с необходимостью немедленного определения неисправного состояния объекта.

Метод Байеса.

Среди методов технической диагностики метод, основанный на обобщенной формуле Байеса, занимает особое место благодаря простоте и эффективности.

Имеет он и недостатки: большой объем предварительной информации, угнетение редко встречающихся диагнозов. Однако в случаях, когда объем статистических данных, позволяет применить метод Байеса, его целесообразно использовать как один из наиболее эффективных и надежных методов.

Основы метода.

Метод основан на простой формуле Байеса. Если имеется диагноз D_i и простой признак k_j, встречающийся при этом диагнозе, то вероятность совместного появления событий (наличие у объекта состояния D_i и признака k_j)

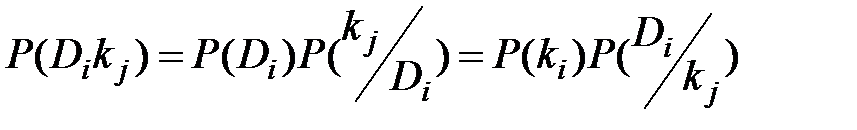. (3.1)

Из этого равенства вытекает формула Байеса

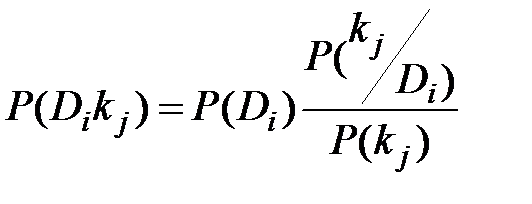. (3.2)

Очень важно определить точный смысл всех входящих в эту формулу величин. 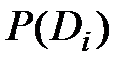- вероятность диагноза D_i, определяемая по статистическим данным (априорная вероятность диагноза). Так, если предварительно обследовано N объектов и у N_i объектов имелось состояние D_i, то

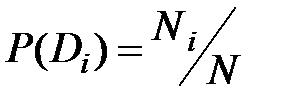. (3.3)

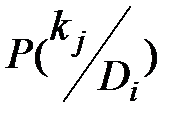вероятность появления признака k_j у объектов с состоянием D_i. Если среди N_iобъектов, имеющих диагноз D_i у N_ij, проявился признак k_j, то

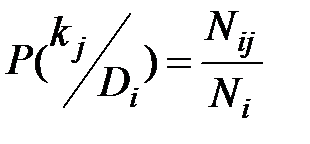. (3.4)

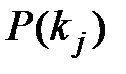- вероятность появления признака k_j во всех объектах независимо от состояния (диагноза) объекта. Пусть из общего числа N объектов признак k_jбыл обнаружен у N_jобъектов, тогда

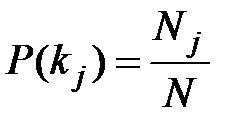. (3.5)

Для установления диагноза специальное вычисление 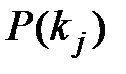не требуется. Как будет ясно из дальнейшего, значения 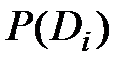, , 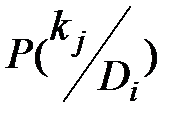известные для всех возможных состояний, определяют величину .

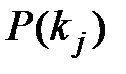В равенстве (3.2) 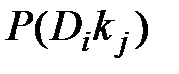- вероятность диагноза D_i после того, как стало известно наличие у рассматриваемого объекта признака k_j (апостериорная вероятность диагноза).

Обобщенная формула Байеса. Эта формула относится к случаю, когда обследование проводится по комплексу признаков K, включающему признаки k₁, k_2, …k_ν. Каждый из признаков k_j имеет m_j разрядов (k_j1, k_j2, …k_js, …, k_jmj). В результате обследования становится известной реализация признака 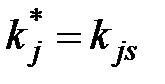и всего комплекса признаков K^*. Индекс * означает конкретное значение (реализацию признака). Формула Байеса имеет вид

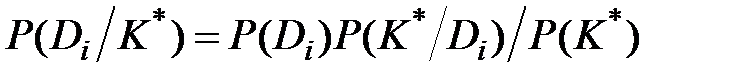, i=1, 2, …, n, (3.6)

где 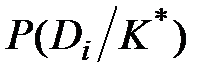- вероятность диагноза D_iпосле того, как стали известны результаты обследования по комплексу признаковК; 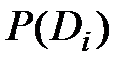- предварительная вероятность диагноза D_i (по предшествующей статистике).

Формула 3.6 относится к любому из n возможных состояний (диагнозов) системы. Предполагается, что система находится только в одном из указанных состояний и потому

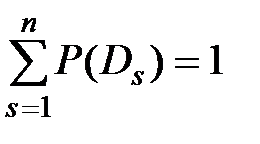. (3.7)

В практике нередко существуют несколько состояний A₁, …A_r, причем некоторые могут встретиться в комбинации друг с другом. Тогда в качестве различных диагнозов D_i следует рассматривать отдельные состояния D₁=A₁,…D_r=A_r и их комбинации D_r+1=A₁^A₂, … и т.п.

Если комплекс признаков состоит из ν признаков, то

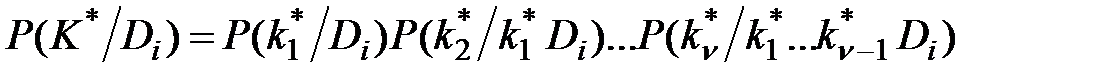, (3.8)

где 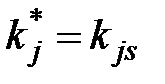- разряд признака, выявившийся в результате обследования.

Для диагностически независимых признаков

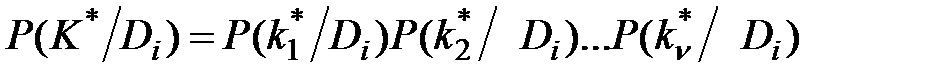. (3.9)

Вероятность появления комплекса признаков K^*

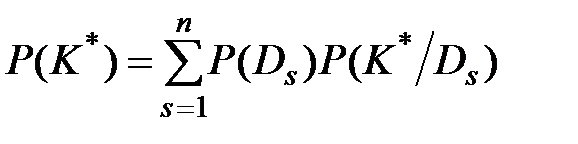. (3.10)

Обобщенная формула Байеса может быть записана

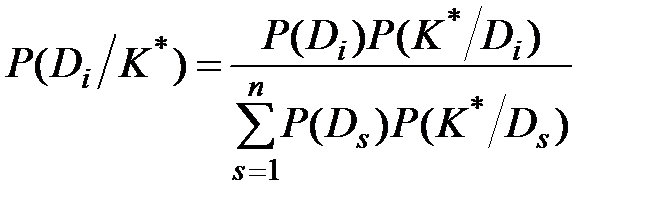, (3.11)

где 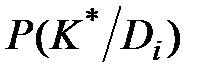определяется равенством 3.8 и 3.9.

Из соотношения 3.11 вытекает 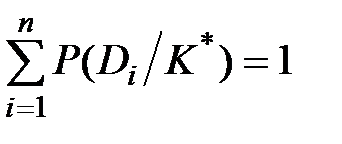, что, разумеется, и должно быть, так как один из диагнозов обязательно реализуется, а реализация двух диагнозов невозможна.

Диагностическая матрица.

Для определения вероятности диагнозов по методу Байеса необходимо составить диагностическую матрицу, которая формируется на основе предварительного статистического материала. В таблице содержатся вероятности разрядов признаков при различных диагнозах. Если признаки двухразрядные (да - нет), то в таблице достаточно указать вероятность появления признака 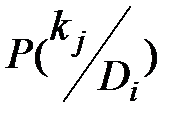. Вероятность отсутствия признака .

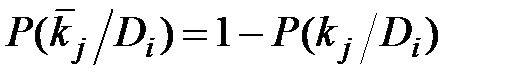В диагностическую матрицу включены априорные вероятности диагнозов.

Диагноз Di	Признаки kj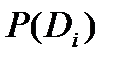
k1	k2	k3
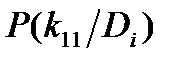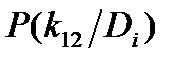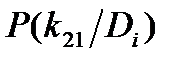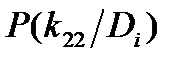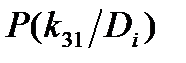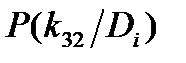D1	0.8	0.2	0.1	0.1	0.2	0.8	0.3
D2	0.1	0.7			0.1	0.9	0.1
…	…	…	…	…	…	…	…

Поясним метод Байеса. Например, при наблюдении за трансформатором проверяются два признака: k₁- повышение температуры обмоток трансформатора и k₂ - уровень шума, создаваемый трансформатором. Предположим, что появление этих признаков связано с неисправностью трансформатора. При нормальном состоянии трансформатора (состояние D₃) признак k₁ не наблюдается, а признак k₂ наблюдается в 5% случаев. На основании статистических данных известно, что 80% трансформаторов вырабатывает ресурс в нормальном состоянии, 5% имеют состояние D₁ и 15% - состояние D₂. известно также, что признак k₁ встречается при состоянии D₁ в 20%, а при состоянии D₂ в 40% случаев; признак k₂ при состоянии D₁ встречается в 30%, а при D₂ в 50% случаев. Сведем данные в диагностическую таблицу.

Di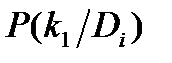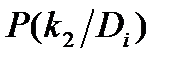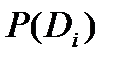
D1 D2 D3	0.2 0.4 0.0	0.3 0.5 0.05	0.05 0.15 0.80

Вероятность состояния, когда обнаружены оба признака определяем по формуле (3.11),

.

,

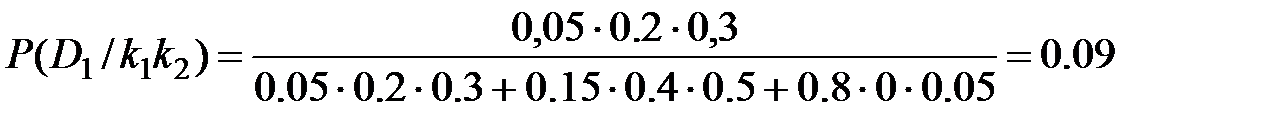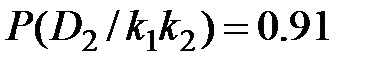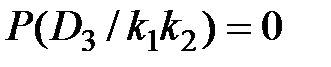
Признак k₁ отсутствует, присутствует признак k₂. Отсутствие признака k₁ есть признак наличия 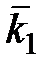(противоположное событие), причем .

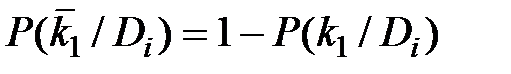Для расчета также применяют формулу (3.11), но

Наши рекомендации