Утверждение 11. Разложение определителя по произвольной строке.

Для определителя матрицы 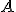справедлива формула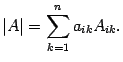

Пример. Вычислите .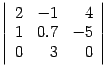

Решение. Воспользуемся разложением по третьей строке, так выгоднее, поскольку в третьей строке два числа из трех - нули. Получим

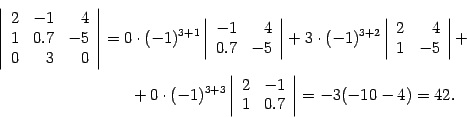
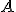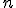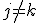Утверждение 12. Для квадратной матрицы порядка при выполнено соотношение .

Утверждение 13. Все свойства определителя, сформулированные для строк (утверждения 1 - 11), справедливы и для столбцов, в частности, справедливо разложение определителя по j-ому столбцу 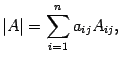и равенство 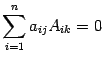при .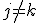

Утверждение 14. Определитель треугольной матрицы равен произведению элементов ее главной диагонали.

Следствие. Определитель единичной матрицы равен единице, .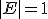

Вывод. Перечисленные выше свойства позволяют находить определители матриц достаточно высоких порядков при сравнительно небольшом объеме вычислений. Алгоритм вычислений следующий.

Алгоритм создания нулей в столбце. Пусть требуется вычислить определитель 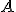порядка 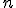. Если 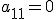, то поменяем местами первую строку и любую другую, в которой первый элемент не нуль. В результате определитель 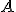, будет равен определителю новой матрицы с противоположным знаком. Если же первый элемент каждой строки равен нулю, то матрица 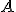имеет нулевой столбец и по утверждениям 1, 13 ее определитель равен нулю.

Итак, считаем, что уже в исходной матрице 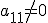. Первую строку оставляем без изменений. Прибавим ко второй строке первую строку, умноженную на число 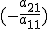. Тогда первый элемент второй строки будет равен .

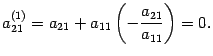Остальные элементы новой второй строки обозначим 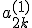, 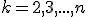. Определитель новой матрицы по утверждению 9 равен . Первую строку умножим на число 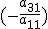и прибавим к третьей. Первый элемент новой третьей строки будет равен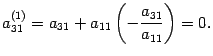

Остальные элементы новой третьей строки обозначим 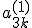, 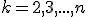. Определитель новой матрицы по утверждению 9 равен .

Процесс получения нулей вместо первых элементов строк продолжим дальше. Наконец, первую строку умножим на число 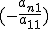и прибавим к последней строке. В результате получается матрица, обозначим ее 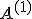, которая имеет вид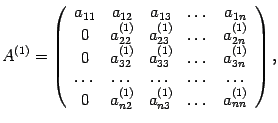

причем 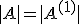. Для вычисления определителя матрицы 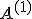используем разложение по первому столбцу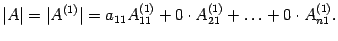

Так как 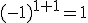, то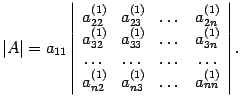

В правой части стоит определитель матрицы порядка 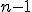. К нему применим тот же алгоритм, и вычисление определителя матрицы сведется к вычислению определителя матрицы порядка 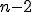. Процесс повторяем до тех пор, пока не дойдем до определителя второго порядка, который вычисляется по определению.

Если матрица 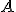не обладает какими-то специфическими свойствами, то заметно уменьшить объем вычислений по сравнению с предложенным алгоритмом не удается. Еще одна хорошая сторона этого алгоритма - по нему легко составить программу для компьютера для вычисления определителей матриц больших порядков. В стандартных программах вычисления определителей используется этот алгоритм с не принципиальными изменениями, связанными с минимизацией влияния ошибок округления и погрешностей входных данных при вычислениях компьютера.

Пример. Вычислите определитель матрицы .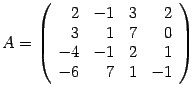

Решение. Первую строку оставляем без изменения. Ко второй строке прибавляем первую, умноженную на число :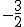

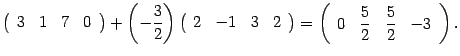
Определитель не меняется. К третьей строке прибавляем первую, умноженную на число :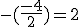

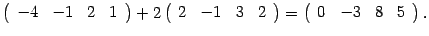
Определитель не меняется. К четвертой строке прибавляем первую, умноженную на число :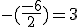

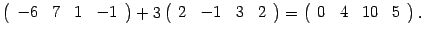
Определитель не меняется. В результате получаем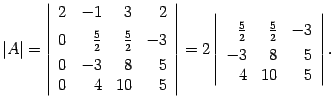

По тому же алгоритму считаем определитель матрицы порядка 3, стоящий справа. Первую строку оставляем без изменений, ко второй строке прибавляем первую, умноженную на число :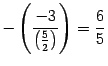

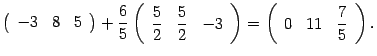
К третьей строке прибавляем первую, умноженную на число :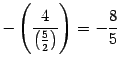

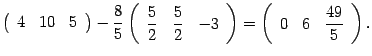
В результате получаем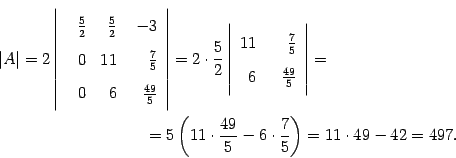

Ответ. .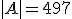

Замечание. Хотя при вычислениях использовались дроби, результат оказался целым числом. Действительно, используя свойства определителей и то, что исходные числа - целые, операций с дробями можно было бы избежать. Но в инженерной практике числа крайне редко бывают целыми. Поэтому, как правило, элементы определителя будут десятичными дробями и применять какие-то ухищрения для упрощения вычислений нецелесообразно.

СОДЕРЖАНИЕ

Лабораторное занятие № 1. Определение количественных показателей надежности систем по результатам испытания…………………………………………… 3

Лабораторное занятие № 2. Исследование надежности невосстанавливаемых систем с различными способами резервирования. 10

Лабораторное занятие № 3. Исследование надежности восстанавливаемых резервированных систем…….…………………….. 25

Лабораторное занятие № 4. Исследование надежности дискретных систем с восстанавливающими органами……….…………. 45

Лабораторное занятие № 5. Исследование соотношения безотказности и безопасности одноканальной и двухканальной систем……………………..………………………... 52

Лабораторное занятие № 6. Исследование влияния технического обслуживания (профилактики) на надежность систем….……..... 60

Кирюнин Александр Игоревич

Расчет надежности систем обеспечения движения поездов

Методические указания к лабораторным занятиям

по дисциплине: «Основы теории надежности»

Редактор

Техническое редактирование и корректура

Подписано в печать 00.00.00 г. Формат 60´84/16.

Бумага офсетная. Ризография. Усл. печ. л. 3,02.

Уч.–изд. л. 0,00. Тираж 100. Изд. № 000. Заказ № .

ФГБОУ ВПО «Ростовский государственный университет путей сообщения».

Ризография ФГБОУ ВПО РГУПС.

Адрес университета: 344038, Ростов на-Дону, пл. Ростовского стрелкового полка народного ополчения, д. 2.