Лекция 10. «Основы расчёта систем массового обслуживания»
План лекции:
Графы состояний СМО
10.2. Уравнения академика А.Н. Колмогорова
Вывод основного уравнения надёжности с помощью ТМО
Графы состояний СМО
В любой системе массового обслуживания, реализуемой в виде какого-либо физического устройства, протекает случайный процесс и система мгновенно переходит из одного дискретного состояния в другое. Будем считать, что переходы СМО из состояния в состояние происходят под воздействием каких-то потоков событий. В теории надёжности это, например, могут быть потоки отказов и потоки восстановления.
Случайный процесс с дискретными состояниями и непрерывным временем называютмарковским, если для любого момента времени 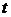 условные вероятности
условные вероятности 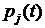 всех состояний
всех состояний 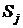 системы массового обслуживания в будущем
системы массового обслуживания в будущем 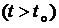 зависят только от того, в каком состоянии
зависят только от того, в каком состоянии  находится СМО в настоящем
находится СМО в настоящем 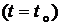 , но не зависят от того, когда и каким образом она пришла в это состояние [3]. В частности, если поток пуассоновский, то процесс перехода СМО из состояния в состояние будет марковским.
, но не зависят от того, когда и каким образом она пришла в это состояние [3]. В частности, если поток пуассоновский, то процесс перехода СМО из состояния в состояние будет марковским.
Состояния системы можно описать как качественно, то есть словами, так и количественно, обычно через вероятность нахождения системы в этих состояниях.
Анализ СМО удобно проводить, используя граф состояний – наглядную схему переходов системы из одного состояния в другое. Состояния  системы на графе представляют в виде квадратов или прямоугольников (вершин графа) и обозначают символами
системы на графе представляют в виде квадратов или прямоугольников (вершин графа) и обозначают символами  , где
, где 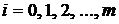 – порядковый номер состояния (рис. 10.1).
– порядковый номер состояния (рис. 10.1).
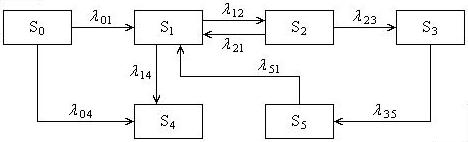
Рис. 10.1. Граф состояний СМО
Граф состояний – ориентированный граф, у которого рёбра (линии произвольной формы, соединяющие вершины), имеют вид стрелок, указывающих направление перехода. Около рёбер удобно проставлять символы интенсивности переходов. Первый индекс у символа указывает номер состояния, из которого происходит переход, второй индекс – номер состояния, в которое осуществляется переход.
Состояния, из которых система может только выйти, а войти обратно – нет, называютисточниками заявок ( 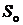 на рис. 10.1). Это понятие имеет смысл начального состояния системы, то есть состояния при
на рис. 10.1). Это понятие имеет смысл начального состояния системы, то есть состояния при  . Обычно бывает одно начальное состояние и его обозначают символом
. Обычно бывает одно начальное состояние и его обозначают символом 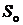 . Реальные источники заявок, как правило, не являются состояниями СМО и поэтому на графе состояний не отображаются.
. Реальные источники заявок, как правило, не являются состояниями СМО и поэтому на графе состояний не отображаются.
Состояние СМО называютконечнымили поглощающим, если система перейти в него может, а выйти из него – нет (например, состояние  на рис. 10.1).
на рис. 10.1).
Состояние  , из которого СМО может непосредственно перейти в другое
, из которого СМО может непосредственно перейти в другое 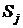 , называютсоседним по отношению к
, называютсоседним по отношению к  и на графе изображают ребром (стрелкой), направленным из
и на графе изображают ребром (стрелкой), направленным из  в
в 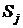 . Состояния
. Состояния  и
и 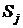 называютсоседними, если существует возможность непосредственного перехода из одного состояния в другое и обратно. На графе состояний эти вершины должны быть соединены двумя противоположно направленными рёбрами.
называютсоседними, если существует возможность непосредственного перехода из одного состояния в другое и обратно. На графе состояний эти вершины должны быть соединены двумя противоположно направленными рёбрами.
Каждое состояние  СМО можно описать вероятностью
СМО можно описать вероятностью 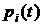 , т.е. вероятностью того, что в момент времени
, т.е. вероятностью того, что в момент времени 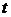 система будет находиться в состоянии
система будет находиться в состоянии  . Для СМО с дискретными состояниями сумма вероятностей состояний в любой момент времени равна единице:
. Для СМО с дискретными состояниями сумма вероятностей состояний в любой момент времени равна единице:

где 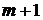 – количество возможных состояний СМО.
– количество возможных состояний СМО.
После начала работы в СМО имеет место переходный процесс. По истечении достаточно большого промежутка времени режим работы СМО будет установившимся (стационарным). Поэтому в начальный момент времени, условно равный нулю, считают, что 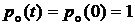 , а вероятности всех остальных состояний равны нулю, т.е.
, а вероятности всех остальных состояний равны нулю, т.е. 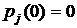 , причём
, причём 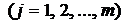 . Если в СМО имеется одно конечное состояние
. Если в СМО имеется одно конечное состояние 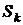 , то в установившемся режиме вероятность
, то в установившемся режиме вероятность 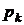 будет равна 1, а всех остальных состояний – 0. Если в СМО конечного состояния нет, то в установившемся режиме все вероятности
будет равна 1, а всех остальных состояний – 0. Если в СМО конечного состояния нет, то в установившемся режиме все вероятности 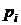 будут постоянными величинами, зависящими как от СМО (структуры графа), так и от интенсивности переходов из состояния в состояние.
будут постоянными величинами, зависящими как от СМО (структуры графа), так и от интенсивности переходов из состояния в состояние.
10.2. Уравнения академика А.Н. Колмогорова
Рассмотрим СМО, имеющую 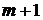 возможное состояние. Будем считать, что для любой пары состояний
возможное состояние. Будем считать, что для любой пары состояний  и
и 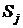 известны интенсивности
известны интенсивности 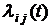 и
и 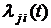 пуассоновского потока событий, переводящего систему из одного состояния в другое и обратно. Интенсивности равны нулю, если непосредственный переход из одного состояния в другое невозможен.
пуассоновского потока событий, переводящего систему из одного состояния в другое и обратно. Интенсивности равны нулю, если непосредственный переход из одного состояния в другое невозможен.
Обозначим через 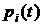 вероятность того, что в момент времени
вероятность того, что в момент времени 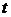 система находится в состоянии
система находится в состоянии  . Придадим времени
. Придадим времени 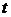 приращение
приращение 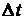 и найдём вероятность
и найдём вероятность 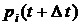 того, что в момент
того, что в момент 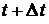 система также будет находиться в состоянии
система также будет находиться в состоянии  .
.
Это событие может произойти, если:
1) в момент времени 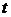 система уже находилась в состоянии
система уже находилась в состоянии  и за время
и за время 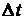 не вышла из него, т.е. не успела перейти в другое состояние, либо,
не вышла из него, т.е. не успела перейти в другое состояние, либо,
2) в момент времени 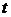 система находилась в одном из соседних состояний
система находилась в одном из соседних состояний 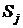 и за время
и за время 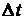 перешла из него в интересующее нас состояние
перешла из него в интересующее нас состояние  .
.
Предположим, что в момент времени 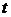 система находится в состоянии
система находится в состоянии  . Условная вероятность
. Условная вероятность 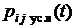 перехода СМО из состояния
перехода СМО из состояния  в соседнее
в соседнее 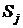 за время
за время 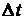 равна произведению интенсивности перехода
равна произведению интенсивности перехода 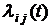 на интервал
на интервал 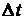 , т.е.
, т.е.
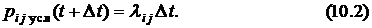
Условная вероятность 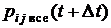 перехода СМО из состояния
перехода СМО из состояния  в любое из соседних
в любое из соседних 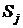 за время
за время 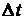 равна сумме условных вероятностей перехода, т.е.
равна сумме условных вероятностей перехода, т.е.
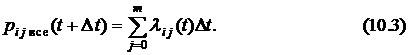
Условная вероятность 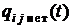 того, что система за интервал
того, что система за интервал 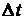 не перейдёт из состояния
не перейдёт из состояния  ни в одно из соседних
ни в одно из соседних 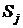 , есть событие противоположное, и поэтому
, есть событие противоположное, и поэтому
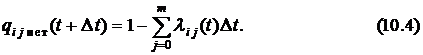
Полная вероятность 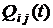 того, что за интервал
того, что за интервал 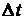 СМО не перейдёт из состояния
СМО не перейдёт из состояния  в любое из соседних
в любое из соседних 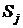 , равна произведению вероятности
, равна произведению вероятности 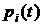 того, что система в момент времени
того, что система в момент времени 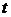 находилась в состоянии
находилась в состоянии  , на условную вероятность невозможности этого перехода. Отсюда получаем формулу
, на условную вероятность невозможности этого перехода. Отсюда получаем формулу
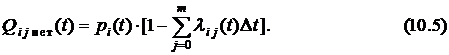
Теперь предположим, что в момент времени 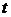 система находится в одном из соседних состояний
система находится в одном из соседних состояний 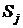 .
.
Условная вероятность 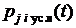 перехода СМО в интервале
перехода СМО в интервале 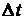 из состояния
из состояния 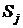 в интересующее нас состояние
в интересующее нас состояние  равна произведению интенсивности перехода
равна произведению интенсивности перехода 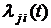 на этот интервал
на этот интервал 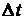 , т.е.
, т.е.
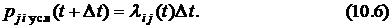
Полная вероятность перехода СМО в интервале 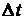 из соседнего состояния
из соседнего состояния 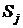 в интересующее нас состояние
в интересующее нас состояние  равна произведению вероятности
равна произведению вероятности 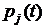 того, что система в момент времени
того, что система в момент времени 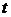 находилась в состоянии
находилась в состоянии 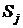 , на условную вероятность такого перехода, т.е.
, на условную вероятность такого перехода, т.е.
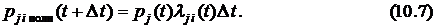
Полная вероятность 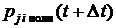 перехода СМО в интервале
перехода СМО в интервале 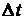 из любого соседнего состояния
из любого соседнего состояния 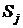 в интересующее нас состояние
в интересующее нас состояние  равна сумме условных вероятностей перехода, т.е.
равна сумме условных вероятностей перехода, т.е.
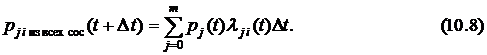
Поэтому вероятность 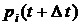 того, что в момент
того, что в момент 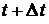 система будет находиться в состоянии
система будет находиться в состоянии  , равна сумме вероятностей (10.5) и (10.8), т.е. того, что система в момент времени
, равна сумме вероятностей (10.5) и (10.8), т.е. того, что система в момент времени 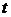 находилась в состоянии
находилась в состоянии  и за интервал
и за интервал 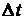 не сумела перейти из него ни в одно из соседних
не сумела перейти из него ни в одно из соседних 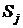 , и того, что система за время
, и того, что система за время 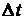 перешла из одного из соседних состояний
перешла из одного из соседних состояний 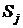 в искомое
в искомое  :
:
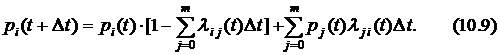
Преобразуем это выражение к виду
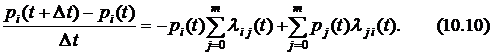
Устремляя 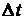 к нулю, в пределе получаем формулу
к нулю, в пределе получаем формулу
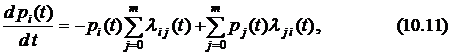
которая носит название уравнения академика А.Н. Колмогорова.
Выражение (10.11) позволяет написать дифференциальное уравнение любого состояния  СМО без вывода по правилу:
СМО без вывода по правилу:
– левая часть уравнения есть производная вероятности 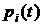 состояния
состояния  по времени,
по времени,
– правая часть уравнения есть сумма произведений вероятностей соседних состояний 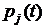 на интенсивности переходов СМО из них в состояние
на интенсивности переходов СМО из них в состояние  и взятого с отрицательным знаком произведения вероятности
и взятого с отрицательным знаком произведения вероятности 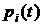 состояния
состояния  на сумму интенсивностей переходов его в соседние состояния.
на сумму интенсивностей переходов его в соседние состояния.
Например, для состояния 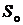 (рис. 10.1) уравнение академика Колмогорова будет записано как
(рис. 10.1) уравнение академика Колмогорова будет записано как
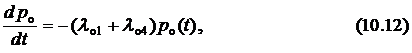
а для 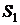
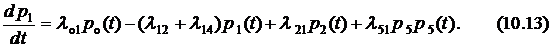
Совокупность уравнений академика Колмогорова для всех состояний СМО образует систему обыкновенных дифференциальных уравнений с переменными коэффициентами, решение которой позволяет найти вероятности состояний СМО. Весьма часто одно из дифференциальных уравнений заменяют нормировочным алгебраическим

так как состояния системы образуют полную группу событий. Систему решают при начальных условиях, т.е. при  , когда вероятности всех состояний СМО обычно бывают известны.
, когда вероятности всех состояний СМО обычно бывают известны.
В установившемся режиме производные равны нулю, и дифференциальные уравнения вида (10.13) переходят в алгебраические.
