Биномиальный закон распределения

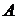Пусть производится независимых опытов, в каждом из которых событие появляется с вероятностью 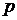и не появляется с вероятностью 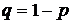. Опыты называют независимыми, если вероятность появления или непоявления события не зависит от того, какие исходы имели другие опыты до этого.

Рассмотрим случай, когда в опытах произойдёт ровно событий .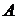

Вероятность появления событий и соответственно непоявления 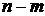этих событий равна произведению соответствующих вероятностей:

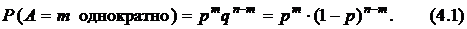
Появление события 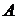ровно раз в опытах может происходить в различной последовательности с непоявлением этого же события. Количество таких чередований есть число сочетаний из элементов по , то есть

Любой вариант появления события 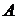ровно раз в опытах имеет одинаковую вероятность, вычисляемую по формуле (4.1). Поэтому для всех возможных сочетаний таких исходов получаем

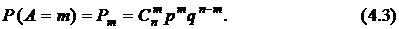
Выражение (4.3) является -м членом -й степени бинома Ньютона:

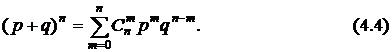
Поэтому такой закон распределения дискретной случайной величины был назван биномиальным.

Если требуется найти вероятность 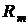того, что событие 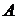появится не менее раз в опытах, то с учётом формулы (4.3) можно получить выражение

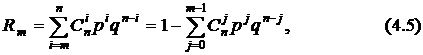
где

есть вероятность противоположного события, то есть вероятность того, что событие 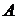появится менее раз в опытах.

Основными числовыми характеристиками биномиального закона распределения являются:

– математическое ожидание

– дисперсия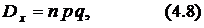

– среднеквадратическое отклонение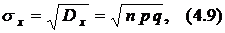

– коэффициент вариации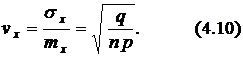

Пример 4.1. Пусть имеется 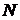одинаковых изделий с интенсивностью отказов 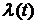у каждого.

Зафиксируем время 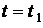так, что 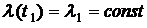, и обозначим вероятность безотказной работы каждого изделия как 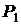, а вероятность отказа соответственно .

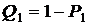Найдём вероятности того, что будут исправны все изделия (то есть не откажет ни одно), что откажет одно, что откажут два и т.д.

Случайное событие здесь – появление отказа с вероятностью 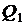. Иначе говоря, согласно обозначениям формул (4.1) и (4.3) имеем соотношение 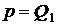. Поэтому вероятность безотказной работы ровно 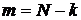изделий или, что то же самое, вероятность появления 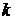отказов могут быть рассчитаны по формуле (4.3), которая примет вид

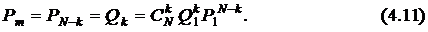
При этом также согласно обозначениям формул (4.1) и (4.3) имеем соотношения , .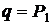

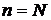Возьмём для конкретности 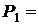0,9. Результаты расчёта по этой формуле приведены в табл. 4.1 и представлены на рис. 4.1.

Таблица 4.1

Вероятности безотказной работы N–k изделий в системе из N штук,

каждое из которых имеет вероятность безотказной работы P₁ = 0,9

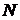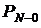	0,9	0,810	0,729	0,6561	0,34868	0,121577
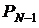	0,1	0,180	0,243	0,2916	0,38742	0,270170
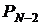	–	0,010	0,027	0,0486	0,19371	0,285180
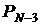	–	–	0,001	0,0036	0,05740	0,171108
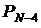	–	–	–	0,0001	0,01116	0,080801
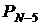	–	–	–	–	0,00149	0,028729

Строго говоря, рис. 4.1 представляет собой множество точек, расположенных на вертикальных линиях, соответствующих различным значениям отказавших устройств 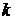. А линии, соединяющие точки друг с другом проведены для удобства выделения точек, относящихся к одному семейству 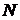одинаковых изделий.

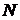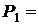В табл. 4.2 приведены числовые характеристики для разного значения количества изделий при 0,9.

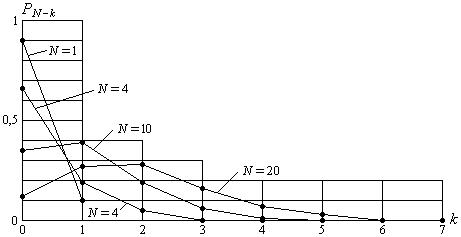
Рис. 4.1. Вероятность безотказной работы 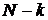устройств при вероятности безотказной работы одного 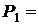0,9

Среднее значение в таблице 4.2 имеет смысл среднего количества отказавших изделий, 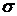– среднеквадратическое отклонение числа отказавших изделий от их среднего значения.

Таблица 4.2