Биномиальный закон распределения случайной величины

Биномиальным называют закон распределения дискретной случайной величины X - числа появлений события в n независимых испытаниях, в каждом из которых вероятность наступления события постоянна. Вероятности pi вычисляют по формуле Бернулли

xk			k	n
Pk	qn	Npqn-1	kCn*pk*qn-k	pn

Мат.ожидание M(X) = np,

дисперсия D(X) = npq,

мода np-q ≤ Mo ≤ np+p,

σ=√npq

В пределе при n→∞ бином. распред. по своим значениям приближается к нормальному с параметрами a=np и σ=√npq В пределе при n→∞ и при p→0 бином. распред. превращается в распред. Пуассона с параметром λ=np.

Распределения случайной величины по Закону Пуассона.

Распределение Пуассона моделирует случайную величину, представляющую собой число событий, произошедших за фиксированное время, при условии, что данные события происходят с некоторой фиксированной средней интенсивностью и независимо друг от друга. При условии p → 0, n →∞ , np → λ  const закон распределения Пуассона является предельным случаем биномиального закона. Так как при этом вероятность p события A в каждом испытании мала, то закон распределения Пуассона называют часто законом редких явлений.

Ряд распределения:

xk			k
Pk	e-λ	λ e-λ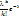

Вероятности вычисляются по формуле Пуассона: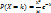

Числовые характеристики: M(X)= λ, D(X)= λ,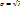

Математическое ожидание дискретной случайной величины и его свойства.

М.дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности: M(X) = x1 p1+ x2 p2+...+ xn pn. Реально на основе данных выборки мы не можем вычислить M(X). Однако эту характеристику можно оценить. В качестве оценки можно использовать среднее арифметическое, то есть M(X) ≈`X. Чем больше объём выборки (число наблюдений), тем точнее эта оценка. Св-ва:

1. М. постоянной величины равно самой постоянной: M(C) = C.

2. Постоянный множитель можно выносить за знак М.: M(CX) = CM(X).

3. М.суммы нескольких случайных величин равно сумме М. слагаемых: M(X+Y+Z) = M(X)+M(Y)+M(Z).

4. М.произведения нескольких взаимно независимых случайных величин равно произведению их М.: M(XЧYЧZ) = M(X)ЧM(Y)ЧM(Z). Все эти свойства имеют большое практическое значение.

Дисперсия, среднее квадратическое отклонение дискретной случайной величины,

Их свойства.

Дисперсией дискретной случайной величины Х называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания: D ( X ) = M ( X - M ( X )) 2. Для вычислений удобнее пользоваться формулой : D ( X ) = M ( X 2 ) - ( M ( X )) 2.

1. D постоянной величины С = 0.

2. Постоянный множитель можно выносить за знак D, возводя в квадрат : D ( CX ) = C ²D ( X ).

3. D суммы нескольких взаимно независимых случайных величин равна сумме D этих величин: D ( X+Y+Z ) = D ( X )+D ( Y )+D ( Z ).

4. D суммы постоянной величины и случайной - равна D случ.величины: D ( C+X ) = D ( X ).

Ср.кв. отклонением случайной величины Х называется корень из D. Ср.кв. отклонение суммы конечного числа взаимно независимых случайных величин равно квадратному корню из суммы квадратов средних квадратических отклонений этих величин.