Формула включений-исключений

Пусть A и B - произвольные множества. Тогда мощность их объединения может быть определена по формуле:

|A È B| = |A| + |B| -|A Ç B|. (1)

Если рассмотреть объединение трех множеств A, B и С, то справедлива следующая формула:

|AÈBÈС|=|A|+|B|+|С|-|AÇB|-|AÇC|-|BÇC|+|AÇBÇC|. (2)

Справедливость каждой их приведенных формул легко может быть проверена с помощью диаграмм Венна для произвольных двух и трех множеств. Для этого достаточно посчитать, сколько раз учитывается в правой и левой части каждого равенства всякий элемент объединения.

Применение приведенных формул при решении конкретных задач может быть оправдано, если нахождение каждого значения в правой части соответствующей формулы проще нахождения всего значения ее левой части.

Считается, что в общем случае объединения множеств устроены сложнее, чем пересечения множеств. Например, множество AÈBÈС в общем случае может рассматриваться как более разнородное, чем каждое из входящих в него множеств A, B и С, поскольку содержать элементы обладающие и не обладающие свойствами элементов множеств A, B и С, в разных комбинациях, в которых достаточно выполнимости лишь одного из свойств элементов этих множеств.

Действительно, в A È B È С могут содержаться элементы, обладающие только свойством элементов множества A. Там же могут содержаться элементы не из A, но обладающие свойствами элементов множеств B или C.

Множества, мощности которых используются в правых частях формул (1) и (2), образованы пересечениями отдельных множеств и поэтому более однородны, поскольку все их элементы обладают одним и тем же свойством, представляемым конъюнкцией свойств элементов множеств входящих в пересечение.

Приведенные формулы (1) и (2) могут быть обобщены на случай объединения произвольного конечного числа множеств так, чтобы свести задачу нахождения мощности объединения множеств к серии задач, связанных с нахождением мощностей нескольких пересечений множеств.

Пусть заданы конечные множества A₁ , ... , A_k и такое число i, что 0 £ i £ k. Обозначим как n_i сумму мощностей всех возможных пересечений по i таких множеств.

Заметим, что n_i является суммой 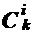слагаемых, так как существует ровно столько различных пересечений по i множеств из k.

ТЕОРЕМА 2.1

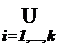| A_i | = n₁ + ... + (-1)^i-1n_i + ... + (-1)^k-1n_k. (1)

Доказательство

Пусть a - это произвольный элемент, входящий в 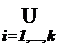A_i .

Покажем, что в левой и правой частях равенства (1) этот элемент множества A учитывается ровно один раз.

Для левой части (1) очевидно, что это так.

Рассмотрим правую часть доказываемого равенства. Предположим, что a содержится в r разных множествах из множеств A₁, ... , A_k. Тогда:

- в n₁ элемент a учтен 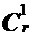раз;

- в n₂ элемент a учтен 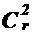раз;

. . .

- в n_r элемент a учтен 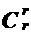раз.

В последующих слагаемых правой части (1) элемент a не учитывается ни разу.

Поэтому в выражении:

n₁ +... + (-1)^i-1 n_i+ ...+(-1)^k-1n_k

элемент aучтен ровно

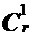+ ... + (-1)^i-1 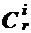+ ... + (-1)^r-1 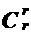раз.

Докажем равенство:

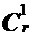+ ... + (-1)^i-1 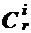+ ... + (-1)^r-1 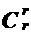= 1.(2)

Перенесем все члены этого равенства в правую часть и с учетом того, что 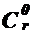= 1, получим:

0= 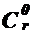- 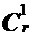+ ... + (-1)ⁱ 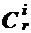+ ... + (-1)^r 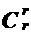. (3)

Воспользуемся формулой бинома Ньютона:

(1 - x)^r = 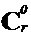- 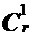x+... + (-1)ⁱ 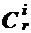xⁱ +...+(-1)^r 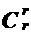x^r.

Очевидно, что формула (3) - частный случай бинома Ньютона для x = 1.

Значит, равенство (2) является справедливым. Поэтому элемент a учитывается в правой части формулы (1) ровно один раз.

Доказательство окончено.

Доказанное в теореме 2.1 соотношение (1) называется формулой включений-исключений.

Рассмотрим пример

В группу артистов входят певцы, танцоры и музыканты.

При этом из них:

1) 9 человек певцы, 12- танцоры и 7 - музыканты;

2) 8 человек одновременно певцы и танцоры, 5 человек

певцы и музыканты, 6 являются танцоры и музыканты;

3) 4 человека одновременно певцы, танцоры и музыканты.

Тогда по формуле включений-исключений общее число людей в группе равно: 9 + 12 + 7 - 8 - 5 - 6 + 4 = 13.

Замечание. Справедливость формулы бинома Ньютона может быть установлена с помощью несложных комбинаторных рассуждений.

Выпишем очевидные соотношения (1 - x)^r = (1-x) . . . (1-x) = а₀ x⁰ + . . . + а_rx^r. Очевидно, что значение коэффициента а_i определяется количеством разных произведений, в которых из i скобок в произведение включается x, а из остальных r-i скобок в произведение входит 1. Поэтому а_i = 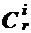. Следовательно,

(1 - x)^r = 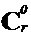- 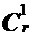x+... + (-1)ⁱ 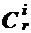xⁱ +...+(-1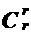)^r x^r.

Упражнение

Сколько существует различных слов в английском языке которые состоят из 7 символов и либо начинаются с WH, либо содержат средний символ R, либо заканчиваются на ING.

Если некоторое множество задано с помощью конечного выражения, составленного из имён конечных множеств, операций над множествами и скобок, то представить мощность такого множеств в виде выражения, образованного суммами и разностями мощностей различных пересечений этих множеств, можно с помощью легко проверяемых правил.

1. | A È B | = | A | + | B | - |AÇB|;

2. | A \ B | = | A | - |AÇB|;

3. A Ç (B È C) = (A Ç B) È (A Ç C);

4. A Ç (B \ C) = (A Ç B) \ (A Ç (B Ç C))

ОТНОШЕНИЯ

ОПРЕДЕЛЕНИЕ И ПРИМЕРЫ ОТНОШЕНИЙ

Пусть заданы множества А и B. Бинарным отношением на этих множествах (или отношением) называется всякое подмножество множества А ´ B. Тo есть отношение на А и B - это произвольное множество пар элементов, первая компонента которых принадлежит А, а вторая - множеству B.

Содержательно всякое отношение состоит из таких пар элементов, между которыми существует определенная смысловая связь. Например, пусть А - это множество людей, а B - множество наименований специальностей. Тогда множество всех таких пар, в которых первая компонента задает конкретного человека, а вторая - специальность, которой такой человек владеет, образует отношение на А 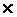B. Для обозначения отношений в дальнейшем будут использоваться строчные символы греческого алфавита: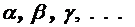

Если (a, b) 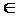r, то в этом случае говорят, что элементы a и b находятся между собой в отношении r.

Для записи факта, что элементы a и b находятся между собой в отношении r, используется также запись arb.

Одним из свойств бинарных отношений на произвольных множествах А и B является возможность взаимно однозначного соответствия между такими отношениями и бинарными предикатами, переменные которых принимают значения из множеств А и B соответственно.

Такое соответствие предикатов и отношений определяется следующими соотношениями.

1. Пусть r Í А 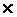B. Ему соответствует такой предикат P(x, y), для которого переменные x и y принимают значения на множествах A и B, что P(x, y) является истинным для тех и только тех наборов значений переменных x и y, которые входят в отношение r.

2. Пусть P(x, y) - некоторый предикат, переменные которого принимают значения из множеств A и B соответственно. Этому предикату можно сопоставить отношение r Í А ´ B, состоящее из тех и только тех элементов множества А 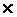B, на которых предикат Pявляется истинным.

Понятие отношения обобщает понятие отображения.

Если 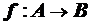- некоторое отображение, то ему можно поставить в соответствие отношение 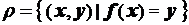. Такое отношение r принято называть графиком отображения f.

Если отношение r образует график некоторого отображения, то для него справедливо следующее свойство. Для каждого элемента x 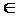A в отношении r содержится ровно одна пара, первая компонента которой равна x.

Отношения, для которых не выполнено последнее свойство, не являются графиками отображений. В этом случае имеет место один из случаев:

1) для некоторого a 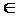A в r нет пары с первой компонентой, равной a;

2) для некоторого a 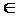A в r содержится не менее двух разных пар, первая компонента которых равна a.

ПРЕДСТАВЛЕНИЕ ОТНОШЕНИЙ

Возможны несколько специальных способов задания отношений.