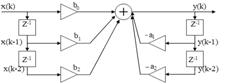
Передаточная функция и прямая структура рекурсивного фильтра 2-го порядка

В z-области основной характеристикой ЛДС является z-изображение импульсной характеристики h(n), которое определяется с помощью Z-преобразования: 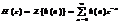и называется передаточной функцией (ПФ). Это математическое определе­ние ПФ. По известному z-изображению импульсная характеристика Н(п) находится с помощью обратного Z-преобразования: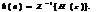

В z-области, согласно теореме о свертке, при нулевых началь­ных условиях соответствует уравнение Y(z) = H(z)X(z), где X(z) и Y(z) —z-изображения воздействия и реакции соответственно. Это позволяет представить передаточную функцию как отношение: 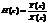и определить ее подобно передаточной функции линейных аналоговых систем.

Передаточной функцией H(z) линейной дискретной системы называется отношение z-изображения реакции к z-изображению воздействия при нуле­вых начальных условиях.

Импульсная характеристика h(n) представляет собой реакцию на воздействие в виде цифро­вого единичного импульса u₀(n), то, подставив z-изображения данных сигналов в Н(z) учитывая, что Z{u₀(n)}=1, получим H(z):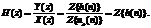

ПФ общего вида: 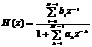представляет собой дробно-рациональную функцию, числитель и знаменатель которой являются многочленами относительно z^-1 порядков (N-1) и (М-1) с вещественными коэффициентами b_i и a_k соот­ветственно.

Порядок передаточной функции равен max {(M-1), (N-1)}.

Как любая дробно-рациональная функция, ПФ характеризуется особыми точками (полюсами) и пулями. Нулями называют значения z, при которых ПФ равна нулю.

Особыми точками (полюсами) называют значения z, при которых знамена­тель ПФ равен нулю. Особые точки и нули ПФ линейных дискретных систем находятся аналогич­но тому, как это делается для ПФ линейных аналоговых цепей. Предвари­тельно необходимо записать H(z) как дробно-рациональную функцию

относительно положительных степеней z, для чего числитель и знаменатель Н(z) следует умножить на z^M-1: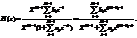

1 Передаточная функция H(z) представляет собой неправильную дробно-рациональную функцию: порядок многочлена числителя равен порядку многочлена знаменателя (N-1) = (М-1). Тогда в результате умножения числителя и знаменателя Н(z) на Z^M-1 имеем: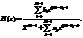

Нулями данной передаточной функции являются корни уравнения числи­теля (корни числителя): 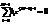, а полюсами — корни уравнения знаменателя (корни знаменателя): .

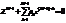Если среди полюсов или нулей встречаются одинаковые, их называют кратными.

2 Передаточная функция H(z) представляет собой правильную дробно-рациональную функцию: порядок многочлена числителя (L-1) меньше порядка многочлена знаменателя (М -1): (L-1)<(M-1), где (L-1) может принимать значения (L-1)=0,1,…, (M-2).

Полюсы передаточной функции H(z) определяются так же, как в первом случае. Что касается нулей, то помимо (L-1) корней числителя добавля­ются нули z=∞, кратность которых равна разности порядков многочле­нов знаменателя и числителя: (M-1)-(L-1) = M-L. Эти нули не считаются информативными, поэтому часто их опускают.

Например, имеем ПФ второго порядка: 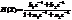. После умножения числителя и знаменателя на z^M-1 = z² получим ПФ: 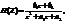представляющую собой правильную дробь, у которой порядок числителя (L-l) = l на единицу меньше порядка знаменателя (М -1) = 2: (M-1)-(L-1)=M-L=1. Следовательно, такая ПФ имеет два нуля: один - корень числителя: 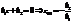и второй — неинформативный: .

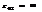Нули и полюсы передаточной функции удобно изображать в виде точек на комплексной z-плоскости. Положение точек определяется их координатами, чаше всего полярными. Нули изображаются кружками (о), а полюсы — звез­дочками ( * ). Совокупность нулей (о) и полюсов (*) на z-плоскости называ­ют картой нулей и полюсов. Такая карта — одна из важнейших графических характеристик ЛДС.

Прямая форма рекурсивных фильтров реализуется непосредственно по его передаточной функции. Она содержит один сумматор, пять умножители и четыре элемента задержки (для создания цепей, соответствующих числителю и знаменателю передаточной функции 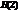используются отдельные элементы задержки).

Недостаток такого способа реализации – сравнительно большое число ячеек памяти, применяемой для рекурсивной и нерекурсивной частей.