Для чего используется и в чем заключается метод серединных произведений?

Данный метод служит для генерации случайных чисел. Число х0 умножается на х1 (они заданы), из полученного результата х2 извлекается середина х2* (это очередное случайное число) и умножается на х1. Из полученного результата х3 извлекается середина х3* (это очередное случайное число) и умножается на х2*. По этой схеме вычисляются все последующие случайные числа.

Для чего используется и в чем заключается метод перемешивания?

Идея метода состоит в следующем. Пусть в ячейке хранится начальное число х0. Циклически сдвигая содержимое ячейки влево на 1/4 длины ячейки, получаем новое число х0*. Точно так же, циклически сдвигая содержимое ячейки х0 вправо на 1/4 длины ячейки, получаем второе число х0**. Сумма чисел х0* и х0** дает новое случайное число х1. Далее х1 заносится в х0, и вся последовательность операций повторяется. В случае, если число, полученное в результате суммирования чисел х0* и х0** полностью не умещается в ячейке х1, то от полученного числа необходимо убрать один «лишний» крайний левый бит.

Для чего используется и в чем заключается линейный конгруэнтный метод?

Данный метод служит для генерации случайных чисел. В этом методе используется операция mod(x, y), возвращающая остаток от деления первого аргумента на второй. Каждое последующее случайное число рассчитывается на основе предыдущего случайного числа по формуле: хi + 1 = mod(k · хi + b, M), где M — модуль (0 < M) q M  p (p – основание системы счисления, q – число разрядов в случайном числе); k — множитель (0 ≤ k < M) k  8t  3 (t – любое целое положительное число; b — приращение (0 ≤ b < M); х0 — начальное значение (0 ≤ х0 < M).

Какие основные свойства функции распределения вероятностей F(x) вам известны?

Функция распределения любой случайной величины обладает следующими свойствами:

· F(x)определена на всей числовой прямой R;

· F(x)не убывает, т.е. если x₁ 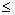x₂, то F(x₁) 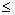F(x₂);

· F(- 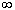)=0, F(+ 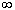)=1,т.е. 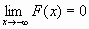и ;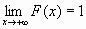

· F(x) непрерывна справа, т.е.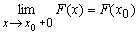

Какую функцию называют плотностью распределения вероятности?

Плотностью распределения вероятности называют производную абсолютно непрерывной функции распределения. Эта функция показывает отношение вероятности того, что случайная величина попадает в малый диапазон значений с центром в заданной точке, к величине этого диапазона.

Что называют математическим ожиданием, выборочным средним случайной величины и

Как они определяется?

Математическим ожиданием случайной величины Х называется число

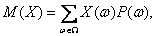
т.е. математическое ожидание случайной величины – это взвешенная сумма значений случайной величины с весами, равными вероятностям соответствующих элементарных событий.

В качестве выборочных средних величин постоянно используют выборочное среднее арифметическое, т.е. сумму значений рассматриваемой величины, полученных по результатам испытания выборки, деленную на ее объем:

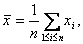
где n – объем выборки, x_i – результат измерения (испытания) i-ого элемента выборки.

23) Что называют дисперсией случайной величины и как она определяется?

Важной характеристикой отклонения или разброса случайной величины от ее среднего значения является дисперсия случайной величины, определяемая как математическое ожидание квадрата отклонения случайной величины X от своего среднего значения:

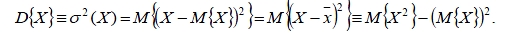
24) Что называют стандартным или среднеквадратичным отклонением и как оно определяется?

25) В чем заключается метод Монте-Карло?

Специальный метод изучения поведения заданной статистики при проведении многократных повторных выборок, существенно использующий вычислительные возможности современных компьютеров. При проведении анализа по методу Монте-Карло компьютер использует процедуру генерации псевдослучайных чисел для имитации данных из изучаемой генеральной совокупности. Процедура анализа по методу Монте-Карло модуля Моделирование структурными уравнениями строит выборки из генеральной совокупности в соответствии с указаниями пользователя, а затем производит следующие действия:

Для каждого повторения по методу Монте-Карло:

Имитирует случайную выборку из генеральной совокупности,

Проводит анализ выборки,

Сохраняет результаты.

После большого числа повторений, сохраненные результаты хорошо имитирует реальное распределение выборочной статистики. Метод Монте-Карло позволяет получить информацию о выборочном распределении в случаях, когда обычная теория выборочных распределений оказывается бессильной.

26) В чем заключается метод исключения (или метода Неймана) для моделирования непрерывных случайных величин?

Пусть случайная величина X определена на конечном интервале (a;b) и плотность ее распределения ограничена, так что f(x)≤M. Тогда, используя пару равномерно распределенных на интервале (0;1) случайных чисел R, осуществляем следующие действия для розыгрыша (моделирования) значения X:

1. Разыгрываем два значения r1 и r2 случайной величины R и строим случайную точку Q с координатами (см. рис. 4): X0=a+r1*(b-a), η=r2*M.

2. Если η>f(X0), то пару значений (r1, r2) отбрасываем и переходим к пункту 1; иначе принимаем X=X0.

Таким образом, определяются координаты случайной точки Q(X0,η) и, если точка окажется под кривой f(x), то абсцисса этой точки принимается в качестве значения случайной величины X=X0=a+r1(b-a) с плотностью распределения f(x). В противном случае точка отбрасывается, определяются координаты следующей точки, и все повторяется.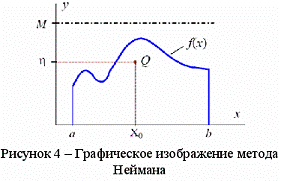

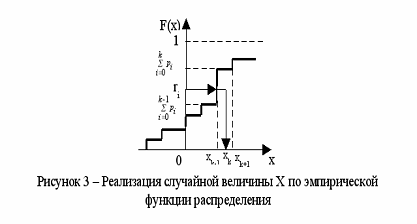
27) Для чего используется и в чем заключается метод обратных функций в ММ?

28) Для чего используется и в чем заключается метод кусочно-линейной аппроксимации?

29) Какая случайная величина имеет распределение Пуассона?

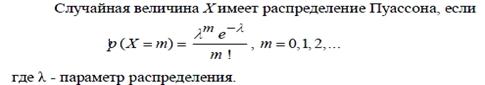
30)Какая случайная величина имеет нормальное распределение?

Случайная величина Х имеет нормальное распределение (или распределение по закону Гаусса), если ее плотность вероятности имеет вид:
,
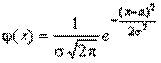где параметры а – любое действительное число и σ >0. Доказано, что параметр а является математическим ожиданием (также модой и медианой), а σ – средним квадратическим отклонением.