Метод серединных квадратов

Пусть имеется 2n-разрядное число, меньшее 1: .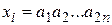

1. Возведем его в квадрат: .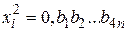

2. Отберем средние 2n разрядов 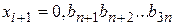, которые будут являться очередным числом псевдослучайной последовательности.

Недостаток метода: наличие корреляции между числами последовательности, в некоторых случаях может отсутствовать.

Конгруэнтные процедуры генерации

Конгруэнтные процедуры представляют собой арифметические операции, в основе которых лежит фундаментальное понятие конгруэнтности.

Два целых числа α и β конгруэнтны или сравнимы по модулю m, m – целое число, тогда и только тогда, когда существует такое целое число k, что α – β = km, т.е. разность α – β делится на m, и числа α и β дают одинаковые остатки от деления на абсолютную величину числа m.

Конгруэнтные процедуры являются чисто детерминированными, так как описываются в виде рекуррентного соотношения (8.3), и имеют вид:

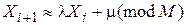, (8.4)

где 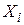, l, m, M – неотрицательные целые числа.

Раскроем рекуррентное соотношение (8.4):

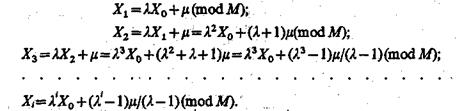(8.5)

Если заданы начальные числа X₀, l, m, M (8.5), то последовательность целых чисел {X_i} составлена из остатков от деления на М членов последовательности .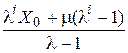

Таким образом, для любого 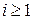справедливо неравенство 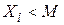, получится последовательность рациональных чисел из единичного интервала (0, 1) .

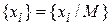Мультипликативный метод

Задается последовательность неотрицательных целых чисел 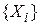, не превосходящих М, рассчитанных по формуле

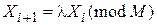, (8.6)

т.е. это частный случай соотношения (8.4) при m = 0.

В силу детерминированности метода получаются воспроизводимые последовательности.

В машинной реализации наиболее удобна версия M = p^g, где p – число цифр в системе счисления в ЭВМ; g – число битов в машинном слове. Тогда вычисление остатка от деления на М сводится к выделению g младших разрядов делимого. Преобразование целого числа 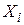в рациональную дробь из интервала 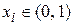осуществляется подстановкой слева от 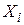двоичной или десятичной запятой.

Алгоритм построения последовательности для двоичной машины M = p^g сводится к выполнению следующих операций:

1. Выбрать в качестве X₀ произвольное нечетное число.

2. Вычислить коэффициент l = 8t ± 3, где t – любое целое положительное число.

3. Найти произведение lX₀, содержащее не более 2g значащих разрядов.

4. Взять g младших разрядов в качестве первого члена последовательности X₁, а остальные отбросить.

5. Определить дробь x₁ = X₁/2^g из интервала (0, 1).

6. Присвоить X₀ = X₁.

7. Вернуться к п. 3.

Смешанный метод

Позволяет вычислить последовательность неотрицательных целых чисел {X_i}, не превосходящих М, по формуле

.

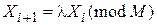Отличием от мультипликативного метода является m ≠ 0.

С вычислительной точки зрения смешанный метод генерации сложнее мультипликативного на одну операцию сложения. При этом возможность выбора дополнительного параметра позволяет уменьшить возможную корреляцию получаемых чисел.

Достоинства метода псевдослучайных чисел:

1. На получение каждого случайного числа затрачивается несколько простых операций, так что скорость генерирования случайных чисел имеет тот же порядок, что и скорость работы ЭВМ.

2. Малый объем памяти ЭВМ для программирования.

3. Любое из чисел легко воспроизвести.

4. Качество генерируемых случайных чисел достаточно проверить один раз.

Подавляющее число расчетов по методу Монте-Карло осуществляется с использованием псевдослучайных чисел. От последовательности случайных чисел, равномерно распределенных в интервале [0, 1], нетрудно перейти к последовательности случайных чисел с произвольным заданным законом распределения.