Раздел 2. ветвления. Множественный выбор

2.1. По десятичной записи числа определить к какому множеству оно относится (N, Z, Q, R, C).

2.2. Даны действительные числа a, b, c (a¹0). Исследовать биквадратное уравнение, т.е. если действительных корней нет, то выдать сообщение «действительных корней нет, в противном случае выдать два или четыре корня.

2.3. Имеется стол прямоугольной формы размером axb (a и b – целые числа, a>b). В каком случае на столе можно разместить большее количество картонных прямоугольников с размерами cxc (c – целое число a>b> c>1): при размещении их стороной вдоль длинной стороны или вдоль короткой. Прямоугольники не должны лежать один на другом и не должны свисать со стола.

2.4. Составьте программу, которая выдает сообщение о кодах ASCII по следующей схеме: если код меньше 32 или равен 127, то выдается сообщение «Управляющие коды». Если значение кода находится в интервале от 48 до 57 выдается сообщение «Код цифры», от 65 до 90 – «Код прописной английской буквы», от 176 до 223 – «Код символы псевдографики»; 128 до 159 – «Код прописной русской буквы»; от 97 до 122 – «Код строчной английской буквы»; от 160 до 175 и от 224 до 239 – «Код строчной буквы»; от 33 до 47, от 58 до 64, от 91 до 96, от 123 до 127, от 240 до 255 – «Код специальных символов».

2.5. «Лото». Известен номер (от 0 до 90) бочонка. Бочонок АВ считается выигрышным, если комбинация A²+B², составленная из цифр, входящих в его номер равна числу N², заданному с клавиатуры. Определите является ли бочонок с заданным номером выигрышным.

2.6. «Школа». Уроки в школе начинаются в 8 часов утра. Длительность урока равна 45 минутам, продолжительность перемены – 10 минут. Школьник находился в школе N часов и M минут. Определить род занятий школьника в указанный момент времени.

(задачи – для повышения рейтинга и как дополнительные для отсутствующих).

Раздел 3. Циклы

3.1. Построить таблицу ASCII-символов.

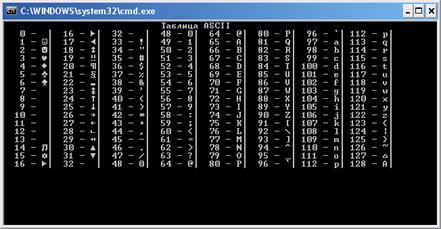
Рисунок 1 – таблица ASCII

3.2. Плотность воздуха r с высотой h убывает по закону r = r₀·e^–h·×z. Определить, на какой высоте плотность будет меньше 1 кг/м³. Считать, что r₀=1,29 кг/м³, z=1,25*10^–4 1/м. Расчет плотности начать от высоты 0 м с шагом 50 м.

3.3. Последовательность чисел Фибоначчи u₁, u₂, …, u_n образуется по закону u₁=1, u₂=1, …, u_i= u_i-1 + u_i-2. Дано натуральное число n>1. Получить u₁, u₂, …, u_n.

3.4. Составьте программу перевода положительных целых чисел из десятичной системы счисления в двоичную систему счисления.

3.5. «Школа». Уроки в школе начинаются в 8 часов утра. Длительность урока равна 45 минутам, продолжительность перемены – 10 минут. Школьник находился в школе N часов и M минут. Определить, какой по счету идет урок, или перемена в указанный момент времени.

3.6. Последовательность Хейса. Рассмотрим некоторое натуральное число n>1.Если оно чётно, то разделим его на 2, иначе умножим на 3 и прибавим 1. Если полученное число не равно 1, то повторяем то же действие (шаг) и т.д., пока не получим 1. Назовем вершиной наибольшее число в полученной при этом последовательности. Для заданного числа построить указанную последовательность, подсчитать число шагов и определить вершину. Например, 7 ® 22 ® 11 ® 34 ® 17 ®52 ® 26 ®13 ® 40 ® 20 ® 10 ® 5 ® 16 ® 8 ® 4 ® 2 ® 1.

3.7. Известно, что значением переменной М является положительное число. Требуется узнать, имеет ли оно симметричную десятичную запись.

(задачи – для повышения рейтинга и как дополнительные для отсутствующих).

Пусть дано решение задачи 3.7.

Присвоим переменной K значение 0. Начнем вычеркивать справа налево одну за другой цифры числа M и приписывать их справа к числу K. Если в некоторый момент окажется, что M=K, то симметричная запись имеется, в противном случае - нет. Однако, представим себе, что M=13231. Если проверять равенство M=K каждый раз после того, как мы перенесли очередную цифру, то равенства не возникнет. Поэтому будем сначала приписывать очередную цифру к K, проверять равенство M=K, вычеркивать эту цифру из записи числа M, и опять проверять равенство М=К.

Процесс переписывания цифр можно было бы делать до тех пор, пока М<>0, однако достаточно продолжать это, пока К<M.

Как Вы считает описанная выше идея решения позволит ли получить достоверный результат? Почему Вы так считаете?

Program Симметрия

Var M, K : Integer

Begin

Write ( 'Введите М = ' ) Read ( M )

K := 0

While K < M Do

Begin

K := K * 10 + M mod 10 (* Приписали цифру *)

If K <> M Then M := M div 10 (* Вычеркнули цифру, если не возникло равенства *)

End

If K = M Then Writeln ('Имеет симметричную запись')

Else Writeln ('Не имеет симметричную запись');

End.

Определите, содержит ли приведенная программа ошибки и если да, то какие.

Раздел 4. Циклы. Ряды.

4.1. Вычислить 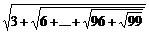при помощи цикла.

4.2. Даны вещественные числа a, x. Вычислить 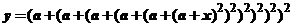при помощи цикла-счетчика.

4.3. Дано натуральное число n. Вычислить 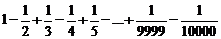двумя способами:

а) последовательно слева направо;

б) последовательно слева направо вычисляются суммы 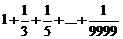и 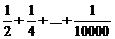, затем втрое вычитается из первого.

Почему при вычислениях на ЭВМ каждым из способов получаются разные результаты?

4.4. Пусть отрезок [a, b] разбит точками на n равных частей. В каждой точке вычисляется значение функции 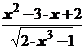. Найдите наибольшее и наименьшее значения функции в этих точках.

4.5. Вычислить с заданной точностью e константу p, используя бесконечный ряд Шарпа: .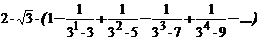

(задачи – для повышения рейтинга и как дополнительные для отсутствующих).

Раздел 5. Массивы.

5.1. Даны натуральное число n, целые числа a₁, a₂, …, a_n. Подсчитать наибольшее число одинаковых следующих подряд чисел.

5.2. В некоторых видах спортивных состязаний выступление каждого спортсмена независимо оценивается несколькими судьями. Затем из всей совокупности оценок удаляются наиболее высокая и наиболее низкая, а для оставшихся оценок вычисляется среднее арифметическое, которое и идет в зачет спортсмену. Если наиболее высокую оценку выставило несколько судей, то удаляется только одна такая оценка. Аналогично поступают с наиболее низкими оценками.

Дано натуральное число n, действительные положительные числа a₁, a₂, …, a_n (n³3). Считая, что числа a₁, a₂, …, a_n – это оценки, выставленные судьями одному из участников соревнования, определить оценку, которая пойдет в зачет этому спортсмену.

5.3. СамРаб1. Решить предыдущую задачу для m спортсменов.

5.4. Дана строка строчных символов английского алфавита. Требуется подсчитать количество появлений каждой буквы алфавита в заданной строке. Символы английского алфавита следует выводить на экран убыванию частоты появления. Задачу решить с использованием массива указанного типа:

Type TArr = array [‘a’..’z’] of byte; inc(A[st[i]])

5.5. У прилавка выстроилась очередь из n покупателей. Время обслуживания продавцом i-го покупателя равно t_i (i=1..n). Пусть даны натуральное n и различные действительные числа t₁, t₂, …, t_n. Получить время пребывания каждого покупателя в очереди. Указать номер покупателя, для обслуживания которого продавцу потребовалось самое малое время.

5.6. В матрице A(m,n) в каждой строке следует удалить все минимальные элементы и сдвинуть остальные элементы к началу последовательности. Для n>=4 или m>=4 предусмотреть заполнение массива случайными числами из диапазона –10 до 10.

(задачи – для повышения рейтинга и как дополнительные для отсутствующих).

Раздел 6. обработка строк

6.1. В тексте слова разделены одним или несколькими пробелами, знаком препинания и пробелом (пробелами). Удалите из предложения все лишние пробелы, т.е. между словами остается только один пробел или знак препинания и пробел.

6.2. Дано натуральное число n. Выбросите из записи этого числа цифры 3 и 7, оставив прежним порядок остальных цифр. Например, из числа 3171507377 должно получиться 1150.

6.3. Дана строка-предложение. Зашифровать ее, поместив вначале все символы, расположенные на четных позициях строки, а затем, в обратном порядке, все символы, расположенные на нечетных позициях (например, строка «Программа» превратится в «ргамамроП»).

6.4. Зашифровать и расшифровать текст (не более 255 символов), используя шифр Цезаря (полученный сдвигом всех букв исходного алфавита на позицию n (1<n<33)).

Например, n=3.

А

Б

В

Г

Д

Е

Ж

З

И

Й

К

Л

М

Н

О

П

Р

С

Т

У

Ф

Х

Ц

Ч

Ш

Щ

Ъ

Ы

Ь

Э

Ю

Я

Г

Д

Е

Ж

З

И

Й

К

Л

М

Н

О

П

Р

С

Т

У

Ф

Х

Ц

Ч

Ш

Щ

Ъ

Ы

Ь

Э

Ю

Я

А

Б

В

6.5. Задан текст, в котором нет вхождений символа ‘(‘ и ‘)’. Выполните сжатие текста: замените всякую максимальную подпоследовательность, составленную из более чем 2 вхождений одного и того же символа, на s (k), где s – повторяемый символ, а k>2 – количество повторений.

6.6. Для большинства существительных, оканчивающихся на -онок, -енок, множественное число образуется от другой основы. Как правило, это происходит по образцу: цыпленок – цыплята, мышонок – мышата и т.д. Имеются слова исключения: ребенок, бесенок, опенок, звонок, позвонок, подонок, бочонок. Дано существительное, оканчивающееся на -онок или -енок. Получите слово во множественном числе.

Раздел 7. Множество

Определение. Гласнымибуквами русского алфавита назовём следующие знаки: а, е, и, о, у, ы, э, ю, я (буква "ё" обычно не входит в литерный тип). Согласными буквами назовём все остальные буквы русского алфавита, кроме букв ь и ъ. Звонкими согласными назовём буквы б, в, г, д, ж, з, й, л, м, н, р, а глухими согласными - буквы к, п, с, т, ф, х, ц, ч, ш, щ.

7.1. Написать программу подсчета количества различных гласных, согласных, звонких согласных, глухих согласных букв в заданном предложении.

7.2. Написать программу для гарантированного ввода вещественного десятичного числа. Например, при вводе строки “abc-8w.9-zE.n-1” программа воспринимает только вещественное число -8.9E-1.