Тема 6. Расчеты при комбинированных видах нагружения (сложное сопротивление).

Косой изгиб.

Задача 7.

Для балки, работающей в условиях косого изгиба (рис.8), необходимо вычислить наибольшие нормальные напряжения в опасном сечении.

Указания. Положение опасного сечения по длине балки может быть выражено неявно. В этом случае опасное сечение определится в результате численного расчета нормальных напряжений в предполагаемых опасных сечениях.

Данные взять из табл.8, схему балки выбрать из рис. 7.

Таблица 8

Цифра шифра	Схема по рис.8	Р1, кН	Р2, кН	а, м	Поперечное сечение
				0,3	№ 20
				0,4	№ 20
				0,5	№ 30
				0,6	№ 24
				0,8	№ 30
				0,6	№ 40
				0,5	№ 24
				0,4	№ 18
				0,3	№ 16
				0,4	№ 40
Буква шифра	д	б	г	в	е

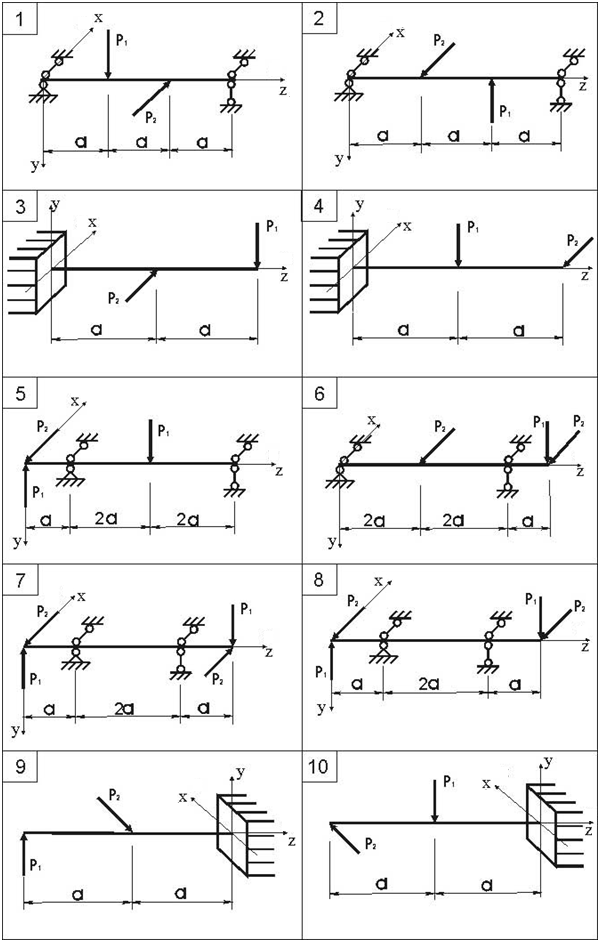
Рис. 7

Внецентренное растяжение – сжатие.

Задача 8.

Колонна, поперечное сечение которой задано (см. рис.8), нагружена сжимающей силой Р, приложенной в точке А.

Требуется:

1) определить положение нейтральной линии в поперечных сечениях колонны;

2) определить наибольшие сжимающие и растягивающие напряжения;

3) построить плоскую эпюру нормальных напряжений.

Данные взять из табл.9, схему рамы выбрать из рис. 8.

Таблица 9

Цифра шифра	Номер схемы	а, см	b, см	Р, кН
Буква шифра	г	е	в	б

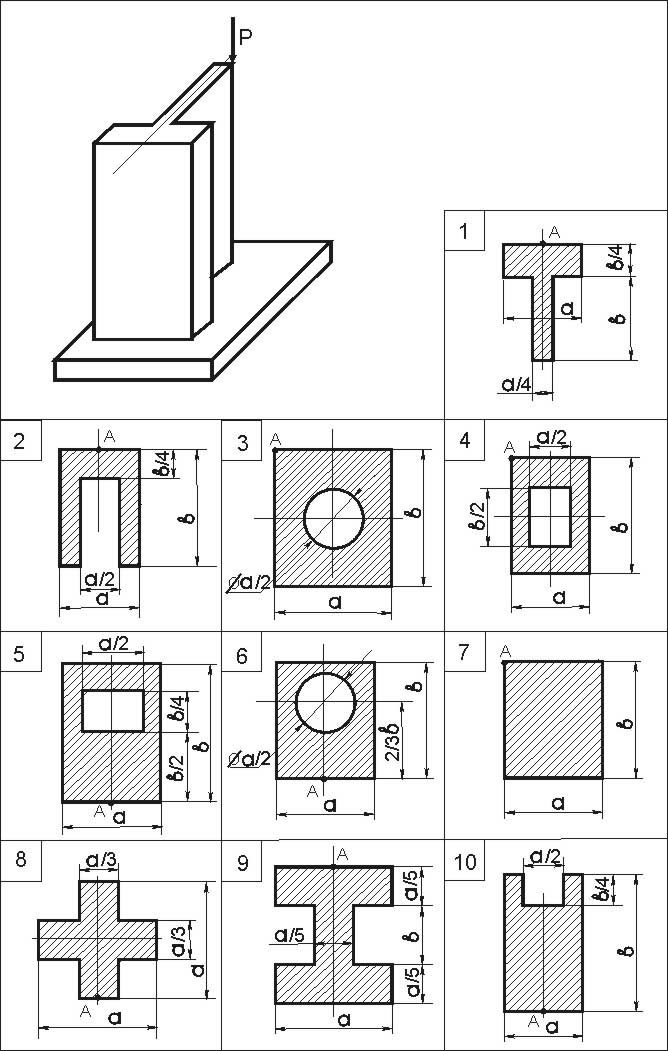
Рис. 8

Изгиб с кручением валов круглого поперечного сечения.

Задача 9.

Стальной вал круглого поперечного сечения вращается со скоростью n об/мин и передаёт мощность N посредством зубчатого колеса с окружным усилием P и шкива, усилия в ведущей и ведомой ветвях которого соответственно равны 2t и t. Ветви ремня параллельны друг другу и наклонены к горизонту под углом α, а окружное усилие действует под углом β.

Требуется:

1) Разложив окружное усилие P и усилия 2t и t ветвей ремня на составляющие в вертикальной и горизонтальной плоскостях, изобразить аксонометрическую расчётную схему вала и указать на ней все внешние силы и моменты (включая предполагаемые реакции связей в опорах);

2) Из уравнений равновесия рассчитать реакции связей в опорах;

3) Построить эпюры изгибающих и крутящих моментов для вала;

4) Установить опасное сечение вала и определить его диаметр d, используя четвёртую теорию прочности.

Данные для решения взять из табл. 10, схему вала – из рис. 9.

Таблица 10

Цифра шифра	Номер схемы	N, кВт	n, об/мин	D1, м	а, м	α, град	β, град	[ σ ], МПа
				0,4	0,25
				0,35	0,3
				0,5	0,4
				0,35	0,2
				0,4	0,15
				0,3	0,2
				0,6	0,25
				0,3	0,35
				0,4	0,4
				0,3	0,2
Буква шифра	д	е	г	д	в	е	г	б

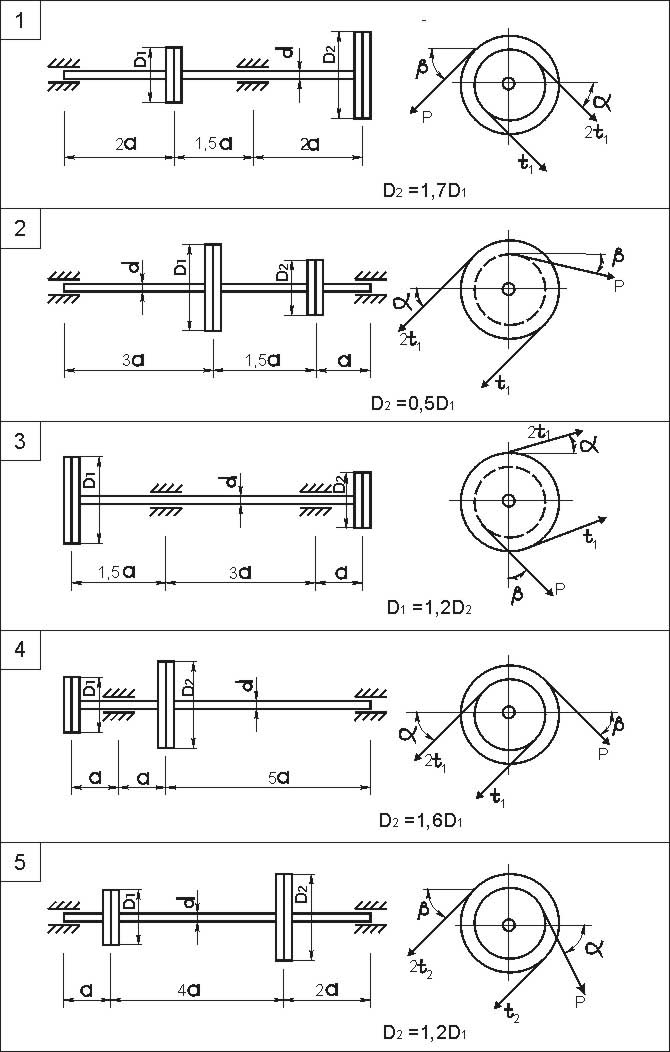
Рис. 9

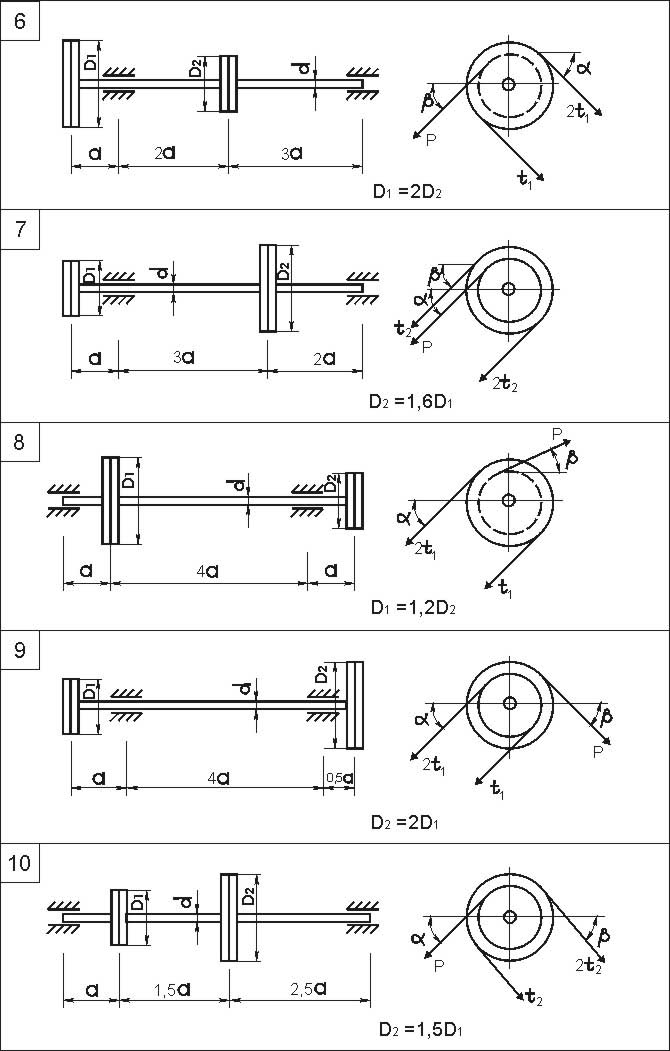
Рис. 9. Окончание

Тема № 7. Расчёт на устойчивость прямолинейного сжатого стержня.

Задача 10.Для стержня заданного сечения, нагруженной продольной силой Р требуется определить:

1) критическую силу Р_кр, используя формулу Эйлера или формулу Ясинского;

2) допускаемую нагрузку Р_доп, используя метод расчёта с помощью коэффициента продольного изгиба φ;

3) коэффициент запаса устойчивости стойки;

Данные для решения взять из табл. 11, схему стержня – из рис. 10.

Указания:

1) стержни изготовлены из стали 3 (допускаемое напряжение при сжатии [σ_с] = 160 МПа);

2) коэффициенты в формуле Ясинского следует принять следующими:

материал	а, МПа	b, МПа
Сталь 3		1,14

3) значения коэффициента φ продольного изгиба даны в приложении 4.

4) в случае, когда гибкость стержня λ >200, длину стержня следует уменьшить так, чтобы его гибкость стала меньше 200.

Таблица 11

Цифра шифра	Схема по рис. 10	Равнополочный уголок	Неравнополочный уголок	Швеллер	d, см	ℓ, м
		80х80х8	75х50х5	№ 12		3,8
		160х160х12	100х63х10	№ 20		4,6
		90х90х80	63х40х8	№ 14
		140х140х10	110х70х8	№ 24		4,8
		100х100х12	80х50х6	№ 10		2,5
		110х110х8	140х90х10	№ 18		3,2
		125х125х12	100х63х8	№ 16		2,2
		70х70х8	125х80х10	№ 22а
		160х160х16	160х100х10	№ 20а		4,2
		180х180х18	180х110х10	№ 24		5,2
Буква шифра	е	д	г	в	б	е

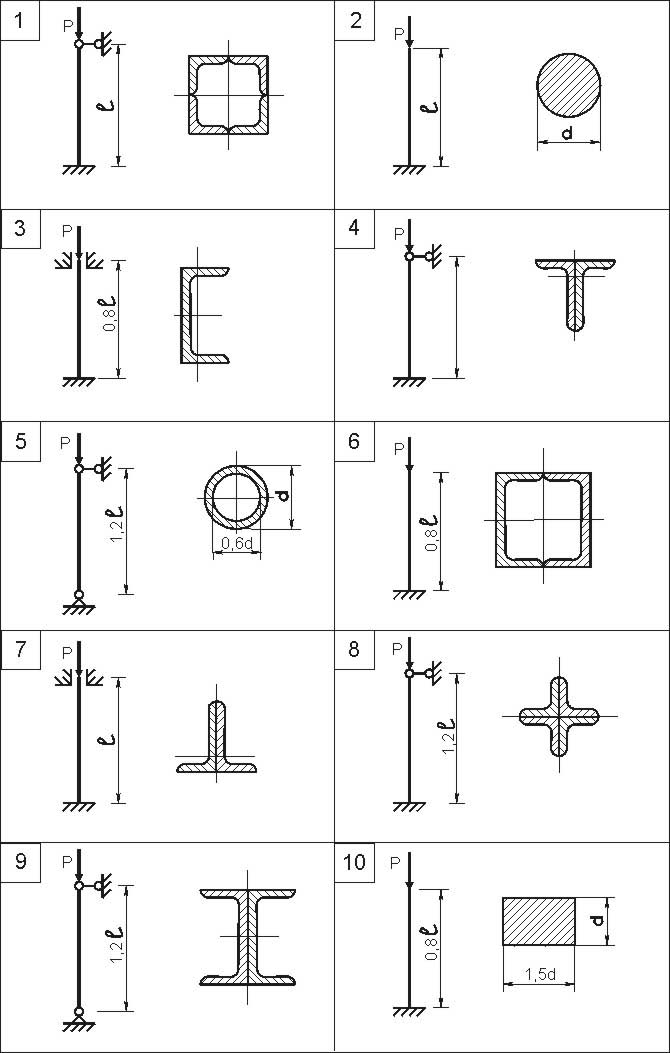
Рис.10